算法与数据结构实验题 2.24 guard

实验任务

部队中共有N个士兵，每个士兵有各自的能力指数Xi，在一次演练中，指挥部确定了M个需要防守的地点，按重要程度从低到高排序，依次以数字1到M标注每个地点的重要程度，指挥部将选择M个士兵依次进入指定地点进行防守任务，能力指数为X的士兵防守重要程度为Y的地点将得到X*Y的参考指数。现在士兵们排成一排，请你选择出连续的M个士兵依次参加防守,使得总的参考指数值最大。

数据输入

输入第一行有两个整数 N, M (1<=N<=1000000，1<=M<=1000)

第二行 N 个整数表示每个士兵对应的能力指数 Xi（1<=Xi<=1000）

数据输出

输出一个整数，为最大的参考指数总和。

输入示例

5 3
2 1 3 1 4

输出示例

17

代码

#include<bits/stdc++.h>
using namespace std;

int n,m,x,a[1000010],sum[1000010];
long long ans;

int main()
{
	scanf("%d%d",&n,&m);
	for(int i=1;i<=n;i++) {
		scanf("%d",&x);
		sum[i]=sum[i-1]+x;
		a[i]=a[i-1]+sum[i];
	}
	for(int i=m;i<=n;i++) ans=max(ans,m*sum[i]-(a[i-1]-a[i-1-m]));
	printf("%lld",ans);
	return 0;
}

思路

本题考查内容为前缀和，关键点在于推式子，怎么样快速地得到一个范围内 $\sum_{1}^{m} i\times X_{i} $ 的值。这里的求和类似于一个阶梯，我们不妨先从总和\(m\times sum[i]\)开始，向下一个个减去\((m-1)\times sum[i-1]\)…\((m-m)\times sum[i-m]\)，那么将这些向下减去的数求和，最终得到的便是\(ans=m\times sum[i]-(a[i-1]-a[i-1-m])\) 示意图如下

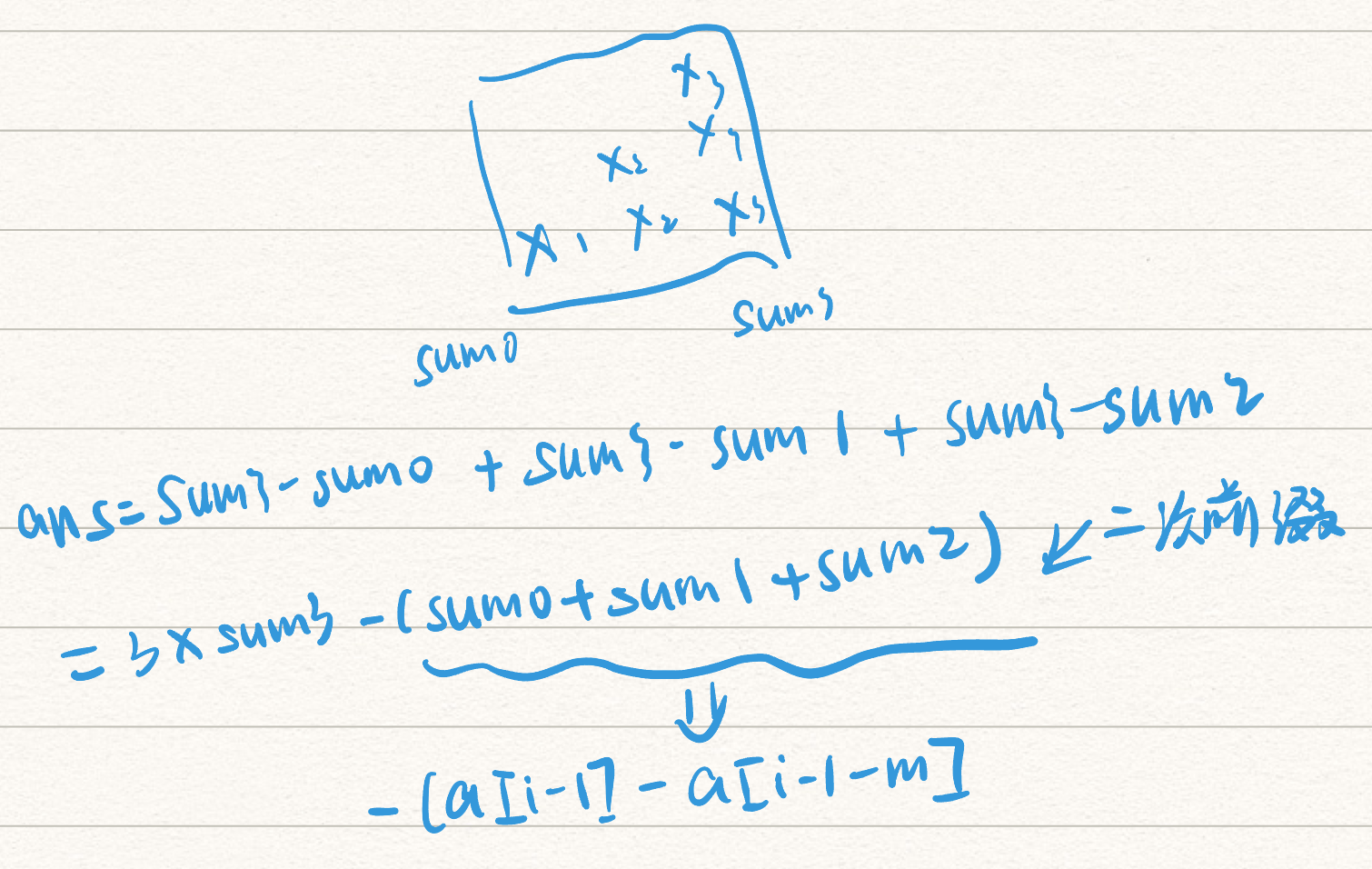
二改：添加示意图，简化代码