51nod1161 Partial Sums

给出一个数组A，经过一次处理，生成一个数组S，数组S中的每个值相当于数组A的累加，比如：A = {1 3 5 6} => S = {1 4 9 15}。如果对生成的数组S再进行一次累加操作，{1 4 9 15} => {1 5 14 29}，现在给出数组A，问进行K次操作后的结果。(每次累加后的结果 mod 10^9 + 7)
Input
第1行，2个数N和K，中间用空格分隔，N表示数组的长度，K表示处理的次数（2 <= n <= 5000, 0 <= k <= 10^9, 0 <= a[i] <= 10^9)
Output
共N行，每行一个数，对应经过K次处理后的结果。每次累加后mod 10^9 + 7。
Input示例
4 2
1
3
5
6
Output示例
1
5
14
29

 

看到这个k如此之大我第一反应就是矩阵快速幂。

但是发现n是5000，矩阵快速幂的复杂度是无法承受的。

然后这个式子又那么特殊，肯定是要特殊地搞一搞。

假如我们定义$f(i,j)$表示对于经过$j$次操作的$ans[x+i]$里面含了多少个$a[x]$。

然后有这个式子:$f(i,j)=\sum\limits_{k=0}^{i} f(k,j-1)$

我们看着这个式子怎么感觉那么有趣，我们先来打个表：

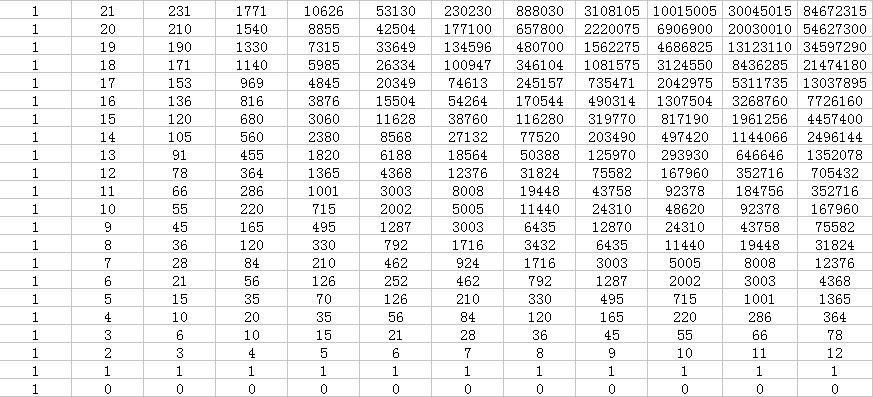
最下面一行是j=0，然后上面是j=1、2、3......

然后我们可以斜着看这个表(就是把这个表转45度)

我们发现是杨辉三角。。。。。

所以说$f(i,j) = C(i+j-1,j-1)$

那么为什么会是这样的呢

$f(i,j) = \sum\limits_{k=0}^{i} f(k,j-1) $

可以转变为

$f(i,j) = f(i,j-1) + f(i-1,j)$

我们对比杨辉三角的式子

$f(i,j) = f(i-1,j-1) + f(i-1,j)$

发现真是玄妙。

 

然后我想到这个地方不知道还是不知道该怎么做真是愚蠢至极。

最后去看了看题解。。。

我们需要求 $C(i+k-1,k-1)$   ($0 \leq i \leq n$)

小学生都知道$ C(n+1,m)=C(n,m) \times \frac{n+1}{n+1-m} $

然后有$C(0+k-1,k-1) = 1$

就可以递推了啊。