51nod 1120 机器人走方格 V3

N * N的方格，从左上到右下画一条线。一个机器人从左上走到右下，只能向右或向下走。并要求只能在这条线的上面或下面走，不能穿越这条线，有多少种不同的走法？由于方法数量可能很大，只需要输出Mod 10007的结果。

 

Input

输入一个数N(2 <= N <= 10^9)。

Output

输出走法的数量 Mod 10007。

Input示例

4

Output示例

10

 

记得这类题曾经看到过，而且当时是这样的：

你一开始在(0,0)，然后你每个时间可以向右上走一步或者向右下走一步。

假如你现在在(x,y)，你可以走到(x+1,y+1)或者(x+1,y-1)，那么走2n步走到(2n,0)并且不能走到x轴下方的方案数是多少。

首先我们知道如果没有越过x轴的限制，方案数就是$C(2n,n)$(一共要走2n步，在其中选n步往上走)

但是我们需要减掉越过了x轴的情况。记得当时给我们看了一个这个图：

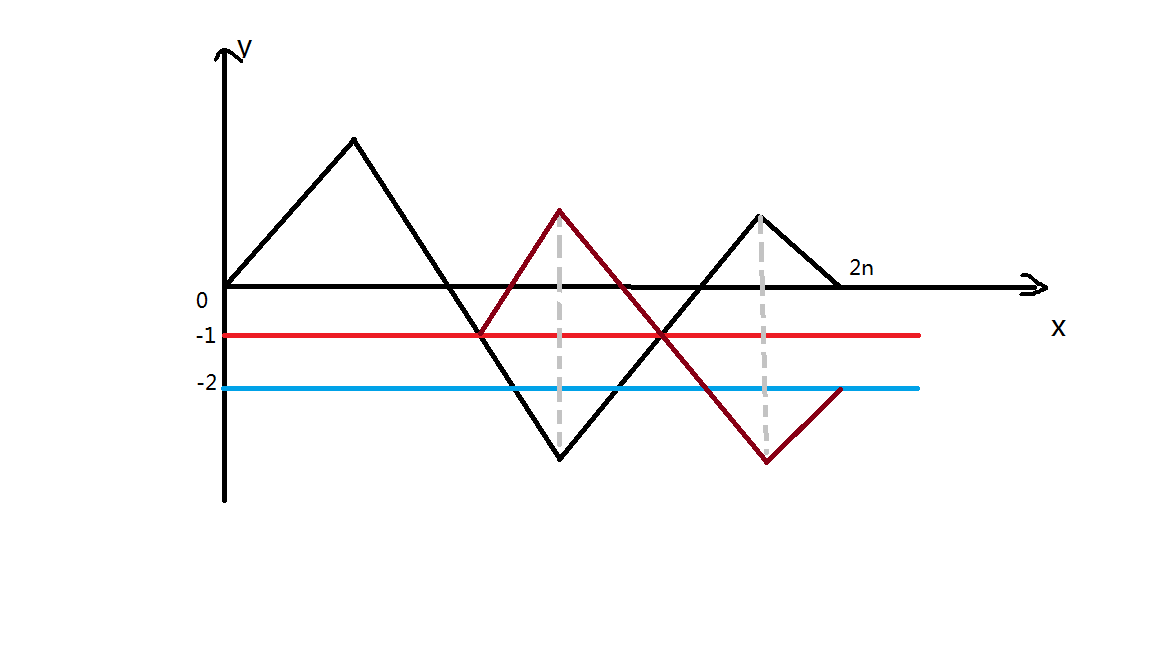
大概意思就是，如果一条路径y坐标到达了-1，那么它就是在x轴下方了

我们把它第一次y坐标到达-1之后的路径以y=-1这条直线为对称轴翻转，那么这条路径的终点就是(2n,-2)

我们观察这被翻转的路径，发现它其实属于一种往右下走次数-往右上走=1的一种路径，这种路径的方案数为$C(2n,n-1)$

所以说，那么走2n步走到(2n,0)并且不能走到x轴下方的方案数是$C(2n,n)-C(2n,n-1)$

我们发现这就是卡特兰数的公式。

 

而机器人走方格这道题也是一样的，只不过他相当于把坐标轴旋转了45度而已。

所以可以直接套组合公式，需要用Lucas定理求。