编译原理实验4——SLR(1)分析器的生成
本篇博客用来记录完成的编译原理实验4的学习过程以及最终成果
实验要求
1.必做功能:
(1)要提供一个源程序编辑界面,让用户输入文法规则(可保存、打开存有文法规则的文件)
(2)检查该文法是否需要进行文法的扩充。
(3)求出该文法各非终结符号的first集合与follow集合,并提供窗口以便用户可以查看这些集合结果。
(4)需要提供窗口以便用户可以查看文法对应的LR(0)DFA图。(可以用画图的方式呈现,也可用表格方式呈现该图点与边的关系数据)
(5)需要提供窗口以便用户可以查看该文法是否为SLR(1)文法。(如果非SLR(1)文法,可查看其原因)
(6)需要提供窗口以便用户可以查看文法对应的SLR(1)分析表。(如果该文法为SLR(1)文法时)
(7)应该书写完善的软件文档
2.选做功能。如果是组队完成实验,则是必做功能,即必须把下面的两个功能也要实现。
(1)需要提供窗口以便用户输入需要分析的句子。
(2)需要提供窗口以便用户查看使用SLR(1)分析该句子的过程。【可以使用表格的形式逐行显示分析过程】
学习
问题:LR(0) 和 SLR(1)是什么
LR(0) 和 SLR(1)都是自底向下的语法分析方法的一个算法
项目
假设有文法
S'->S
S->(S)S|ε
那么下面列举出LR(0)的8个项目(可以把每一个项目看成是旅游地图的一部分,而其中的点是游客当前所处的位置)
S'->.S
S'->S.
S->.(S)
S->(.S)S
S->(S.)S
S->(S).S
S->(S)S.
S->.
每个项目可以看成一个状态。如果某个状态可以通过输入文法中的终结符、非终结符得到新状态,例如
S'->.S ——S——> S'->S.
则称该状态为移进状态;如果某个状态点已经到了末尾,需要原路返回,则称该状态为归约状态,例如
S->S. 为归约项
最终形成一个NFA表,NFA表通过ε闭包的改写则可成为DFA表(一个状态可能有多个项目),通过DFA表就可以对句子进行LR(0)分析(移进归约)。
LR(0)文法:如果一个文法产生的DFA表中的每一个状态包含的都是移进项目或者只有一个归约项,那么该文法成为LR(0)文法。
SLR(1)文法:如果一个文法产生的DFA表中的每一个状态包含的归约项目的Follow集合交集为空和移进的符号不属于任何一个归约项目,则称该文法为SLR(1)文法
实践
项目基于C++实现,可视化是使用QT。所有用到的编程知识点都在此链接
项目地址
文法规则的存储结构
对于下面的文法规则,我们要如何存储呢?
E' -> E
E -> E + n | n
首先给出定义如下:
(1)产生式: 若干条产生式构成一个文法规则。例如E -> E + n | n为一条产生式
(2)key,values: 对于一条产生式来说,->左边的符号我们称作key,右边的符号序列我们称作values。例如,对于产生式E -> E + n | n来说,E为key,E + n | n为values
(3)value: 若干个value构成一个values。例如对于valuesE + n | n来说,|符号分割出了两个value,分别为E + n和n
给出定义之后,接下来就来分析一下具体的存储结构?
(1)对于每个符号(不包括->和|),使用string对象来存储,因为一个符号可以为多个字符。
(2)对于一个value,使用vector< string>对象来存储,因为它本质为string的序列。之所以用vector对象而不用数组,是因为value的大小不确定。
(3)对于一个values,使用vector<vector< string>>来存储,本质上就是value序列。
(4)对于一个文法, 使用map<string, vector<vector< string>>>对象来存储,因为产生式本质为一个键值对,多个键值对就构成一个文法。
既然已经知道了文法的存储结构,下面就需要解决如何把用户输入的文法字符串(转换前需要先进行文法扩充)转换为上面的存储结构。首先我们必须给用户输入文法字符串给予一定的约束,因为不同的输入形式会对应不同的转换算法。我的字符串约束为:
E' -> E\nE -> (E) + n | n
(1)每个产生式用'\n'分割
(2)每一个value用'|'分割
(3)符号之间用' '分割,但是左右括号除外
(4)key为开始符号的产生式必须置于最前面(开始符号会在转换的过程中通过string对象保存起来)
得到了文法的存储结构后,我们可以很容易求得文法规则的非终结符集,通过set< string>对象来存储
所有非终结符的first集合
首先说明一下用原来自顶向下的方法来求first集合是行不通的,因为自底向上的文法规则可以有左递归,该算法无法解决有左递归的情况甚至一些不是左递归的情况。比如下面的文法。
A -> A s | ε
A -> B A | ε
B -> b | ε
所有非终结符first集合的存储结构
(1)一个非终结符的first集合用set< string>来存储
(2)所有非终结符的first集合用map<string, set< string>>来存储,因为通过映射我们可以直接找到某个非终结符的first集合
求解所有非终结符first集合的算法
算法描述如下:
初始化所有非终结符对应的first集合(置为空)
while 存在非终结符的first集合发生改变:
for 产生式 in 文法规则:
定义产生式对应的key, values
for value in values:
for value[k] in value: //遍历value中每一个符号,value[k]中为value的第k个符号(编号从0开始)
定义符号value[k]的first集合为k_first_set
if value[k]为终结符:
k_first_set = {value[k]}
else:
k_first_set = 非终结符value[k]对应的first集合
add k_first_set - {"ε"} to 非终结符key对应的first集合
if "ε" not in k_first_set:
break;
if k == value.size: //value元素的大小
add {"ε"} to 非终结符key对应的first集合
所有非终结符的follow集合
下面算法求解必须在first集合求解完毕后进行
求解所有非终结符follow集合的存储结构
(1)一个非终结符的follow集合用set< string>来存储
(2)所有非终结符的follow集合用map<string, set< string>>来存储,因为通过映射我们可以直接找到某个非终结符的follow集合
求解所有非终结符follow集合的算法
我们需要先定义求解一个符号序列first集合的算法,因为求解所有非终结符的follow集合需要用到
first(符号序列)算法描述如下:
定义空集合set
for s[k] in 符号序列: //遍历符号序列的每一个符号,其中s[k]为符号序列第k个符号(编号从0开始)
求解s[k]的first集合k_set //s[k]如果为终结符就是{s[k]}, 如果为非终结符就在原来的存储first集合的地方获取
add k_set - {"ε"} to set
if "ε" not in k_set:
break;
if k == 符号序列.size:
add {"ε"} to set
return set
求解所有非终结符的follow集合的算法描述如下:
初始化所有非终结符的follow集合(置为空)
while 存在一个非终结符的follow集合发生改变:
for 产生式 in 文法:
定义产生式对应的key, values
for value[k] in values:
if value[k]为非终结符:
add first(value[k+1, ]) to 非终结符value[k]对应的follow集合 //value[k+1, ]是value1的子序列
if "ε" in first(value[k+1, ]):
add 非终结符key对应的follow集合 to 非终结符value[k]对应的follow集合
DFA图、SLR(1)分析表
项目的存储结构
首先给出项目的定义:
项目就是key -> 被加上了'.'的value
例如,对于文法规则
E' -> E
E -> E + n | n
来说,对应的8个项目为
E' -> .E
E' -> E.
E -> .E + n
E -> E. + n
E -> E +. n
E -> E + n.
E -> .n
E -> n.
项目还有不同的类型
形如E -> n.的项目称为归约项, 其'.'在项目最后
形如E -> .n的项目称为移进项, 其'.'不在项目最后
那么,该如何存储一个项目呢?
首先我们发现一个项目由key,value,'.'的位置唯一确定,为了节省存储空间,value可以用在key对应的values下的编号表示
所以我们定义一个数据结构Project来存储项目
Class Project{
string key;
int value_num; //在key对应的values下value的编号
int index; //'.'的位置编号,表示'.'在value中第index个符号前面
int type; //项目的类型: 1为移进项 2为归约项
}
结点的存储结构
首先给出结点的定义:
一个结点如图所示:若个项目的集合为结点
(1)单个结点的存储结构: 因为结点是若干个项目的集合,所以我们使用vector< Project>对象来存储
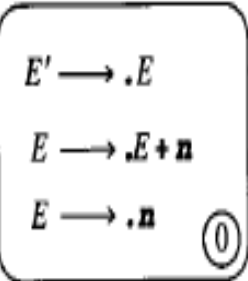
(2)所有结点的存储结构: 用vector<vector< Project>>来存储,这样我们也可以通过vector的下标得到结点编号

注意:结点的存储结构应该使用排序树会更好,因为后面算法有搜索步骤。
移进关系(DFA的图边关系)的存储结构
移进关系就是结点间的转移关系,就是上图中的那些边。存储结构为:
(1)某个结点(作为起点)的转移关系用map<string, int>对象存储,其中string存储移进符号,int存储转移后的结点编号
(2)所有结点(作为起点)的转移关系用map<int, map<string, int>对象来存储,其中int是起点的结点编号,map<string, int>存储着对应结点的转移关系
归约关系的存储结构
归约关系是某个结点的回退操作(与移进相对)。存储结构为:
(1)某个结点(作为回退起点)的归约关系用map<string, int>对象存储,其中string存储导致归约发生的下一个符号(follow),int存储归约项在结点中的编号。
(2)所有结点(作为回退起点)的归约关系用map<int, map<string, int>>对象存储
结点、移进关系、归约关系、判断是否为SLR(1)文法的求解算法
首先通过举例的方式定义扩展这个概念:对于文法规则
E' -> E
E -> E + n | n
项目E' -> .E扩展得到
E' -> .E
E -> .E + n
E -> n
就是把'.'后面的非终结符用其对应的项目('.'在value最前面)来具体化。就像你走到门口推开大门看到里面具体的风景一样。
然后描述算法:
初始化结点序列(只有一个结点, 并且结点只有一个项目,项目=Project(开始符号,0,0,1))
for 结点 in 结点序列:
初始化该结点对应的移进关系 //置为空字典
初始化该结点对应的归约关系 //置为空字典
扩展该结点(中的每一个项目)
for 项目j in 结点:
if 项目为移进项:
定义该项目的转换符号为t
定义移进后的新项目为p
if t未在移进关系的关键字集合里面:
if p in 结点k:
将t:k键值对加入移进关系中
else:
向结点集合插入一个含有p的新结点k
将t:k键值对加入移进关系中
else: //t已经在移进关系的关键字集合里面
获取转移到的结点k
if p not in 结点k:
p加入结点k中
else: //项目为归约项
获取项目j.key对应的follow集合follow
for t in follow:
if t:j 已经存在:
说明文法不是SLR(1)文法 //因为不满足SLR(1)结点中归约项.key的follow集合交集为空的原则
将t:j加入移进关系
for 结点 in 结点序列:
if 结点的移进符号集和归约符号集有交集:
说明文法不是SLR(1)文法 //因为不满足SLR(1)结点中移进符号不存在于该结点中任何一个归约项key的follow集合
用结点、移进关系生成LR(0)DFA图
有了结点序列和所有结点的移进关系,就已经包含了LR(0)DFA图的所有信息,自己想怎么生成就怎么生成
用结点、移进关系、归约关系生成SLR(1)表
有了结点序列和所有结点的移进关系、归约关系,就已经包含了SLR(1)表的所有信息,自己想怎么生成就怎么生成
分析句子
实现句子的分析需要一个分析栈和输入队列,存储结构我选择vector< string>,之所以不用stack和queue,是因为stack和queue没有迭代器,没有办法遍历,而vector只要在使用时给一定约束就可以当作stack或queue使用。
算法描述如下:
定义分析栈为stack,用户队列为queue
初始化stack(0压入栈顶)
初始化queue(用户输入的句子分割成一个个符号后加入queue,最后再加入"$")
for i in range(0, 无穷大):
输出步骤i
输出分析栈
输出输入队列
获取栈顶元素f
获取队列头元素s
if s为结点f的移进字符:
弹出队首元素
t = 结点k由s转换后的结点编号
s、t分别入栈
输出"移进s"
else:
t = 结点f的归约项目编号
得到归约项p
定义p对应的key -> value
if key为开始符号:
输出"接受"
break
if value[0] != "ε":
弹出stack的2*value.size个元素
f = 栈顶元素
s = key
t = 结点k由s转换后的结点编号
s、t入栈
输出"归约key -> value"
运行效果