hiho #1151 : 骨牌覆盖问题·二 （递推，数论）

#1151 : 骨牌覆盖问题·二

时间限制:10000ms

单点时限:1000ms

内存限制:256MB

描述

上一周我们研究了2xN的骨牌问题，这一周我们不妨加大一下难度，研究一下3xN的骨牌问题？
所以我们的题目是：对于3xN的棋盘，使用1x2的骨牌去覆盖一共有多少种不同的覆盖方法呢？
首先我们可以肯定，奇数长度一定是没有办法覆盖的；对于偶数长度，比如2，4，我们有下面几种覆盖方式：

 

提示：3xN骨牌覆盖

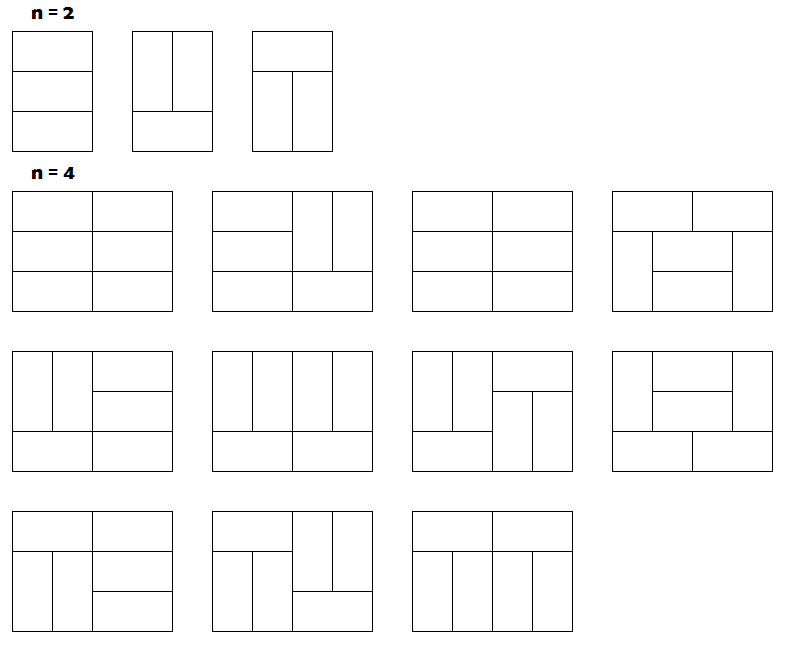
输入

第1行：1个整数N。表示棋盘长度。1≤N≤100,000,000

输出

第1行：1个整数，表示覆盖方案数 MOD 12357

样例输入

62247088

样例输出

4037

 

思路：

当N为基数的时候，肯定覆盖不了。

当N为偶数的时候，对N做除2操作，找出递推公式。

a[0] = 1;
a[1] = 3;
a[2] = 11;

递推公式为：

f(n)=3(f(n-1)+f(n-2))-f(n-3);

 

AC代码：

#include <iostream>
#include <algorithm>
#define mod 12357
using namespace std;

//5324124312
int solve(long long n)
{
    n = n / 2;
    int a[3],t=0;
    a[0] = 1;
    a[1] = 3;
    a[2] = 11;

    if (n < 3)
        return a[n];

    for (int i = 3; i <= n; i++)
    {
        t = (3*a[2] + 3*a[1]-a[0]+mod)%mod;
        a[0] = a[1];
        a[1] = a[2];
        a[2] = t;
    }
    return t;
}

int main()
{
    long long n;
    while (cin >> n) {
        if (n & 1)
            cout << 0 << endl;
        else
            cout << solve(n) << endl;
    }


    system("pause");
    return 0;
}

需要注意的是，有一个取余操作。

t = (3*a[2] + 3*a[1]-a[0]+mod)%mod;   括号内的数需要加上一个Mod，不然可能为负。