Luogu-P2657 [SCOI2009]windy数

 

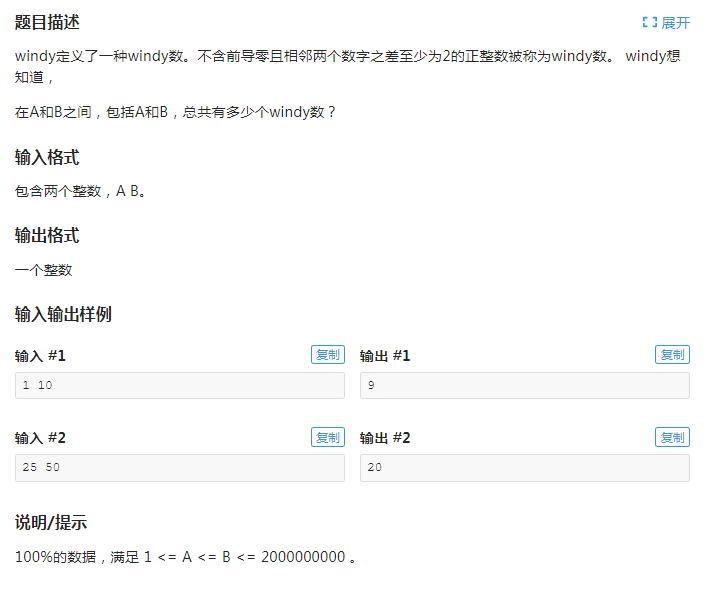
题目

题目链接

 

 

测试得分：　　100

 

 

主要算法 ：　　数位DP

 

 

题干：

　　　数位DP板子

 

 

分析：　　

1. 　　预处理出f[i][j]长度为i且最高位为j的windy数个数

void Init()
{
    FORa(i,0,M) f[1][i]=1;
    FORa(i,2,N)
        FORa(j,0,M)
            FORa(k,0,M)        
                if(abs(j-k)>=2) f[i][j]+=f[i-1][k];//预处理 
}

 

　　2.　　数位DP转移

    int len=0,ans=0,y;
    while(n) s[++len]=n%10,n/=10;
    FORa(i,1,len-1)
        FORa(j,1,M)
            ans+=f[i][j];//位数小于n的位数的，全部累加起来
    FORa(i,1,s[len]-1) ans+=f[len][i];//位数一样但是小于最高位的累加 
    FORs(i,len-1,1)//i从最高位后开始枚举
    {
        FORa(j,0,s[i]-1)//j是i位上的数 
            if(abs(j-s[i+1])>=2)//判断和上一位(i+1)相差2以上)    
                ans+=f[i][j]; //如果是 ans就累加 
        if(abs(s[i+1]-s[i])<2)       break;
    }

　　代码

　　

#include<math.h>
#include<stdio.h>
#include<stdlib.h>
#include<string.h>
#define FORa(i,s,e) for(int i=s;i<=e;i++)
#define FORs(i,s,e) for(int i=s;i>=e;i--)
#define gc pa==pb&&(pb=(pa=buf)+fread(buf,1,100000,stdin),stdin)?EOF:*pa++
#define File(name) freopen(name".in","r",stdin);freopen(name".out","w",stdout);

using namespace std;
char buf[100000],*pa,*pb;
inline int read();

const int N=10,M=9;
int f[N+1][M+1],fpow[N+1],s[N+1];
int a,b;
//f[i][j]代表的是一共有i位，最高位为j的windy数个数 
void Init()
{
    FORa(i,0,M) f[1][i]=1;
    FORa(i,2,N)
        FORa(j,0,M)
            FORa(k,0,M)        
                if(abs(j-k)>=2) f[i][j]+=f[i-1][k];//预处理 
}
int Count(int n)
{
    int len=0,ans=0,y;
    while(n) s[++len]=n%10,n/=10;
    FORa(i,1,len-1)
        FORa(j,1,M)
            ans+=f[i][j];//位数小于n的位数的，全部累加起来
    FORa(i,1,s[len]-1) ans+=f[len][i];//位数一样但是小于最高位的累加 
    FORs(i,len-1,1)//i从最高位后开始枚举
    {
        FORa(j,0,s[i]-1)//j是i位上的数 
            if(abs(j-s[i+1])>=2)//判断和上一位(i+1)相差2以上)    
                ans+=f[i][j]; //如果是 ans就累加 
        if(abs(s[i+1]-s[i])<2)       break;
    }
    return ans;
}
int main()
{
    Init();
    scanf("%d%d",&a,&b);
    printf("%d",Count(b+1)-Count(a));
    return 0;
}
inline int read()
{
    register char c(gc);register int f(1),x(0);
    while(c<'0'||c>'9') f=c=='-'?-1:1,c=gc;
    while(c>='0'&&c<='9') x=(x<<1)+(x<<3)+(c^48),c=gc;
    return x*f;
}

 

总结：

　　1.确定每一个位的数的范围

　　2.状态的确定性