组合数学
一、计数原理
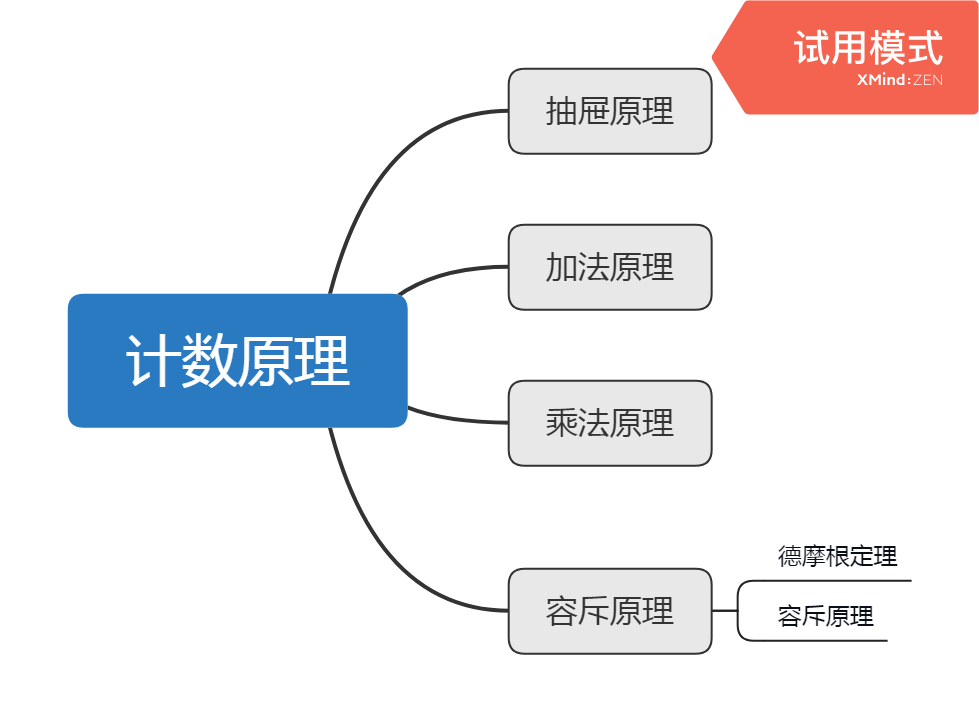
计数原理
抽屉原理
加法原理
乘法原理
容斥原理
德摩根定理
容斥原理
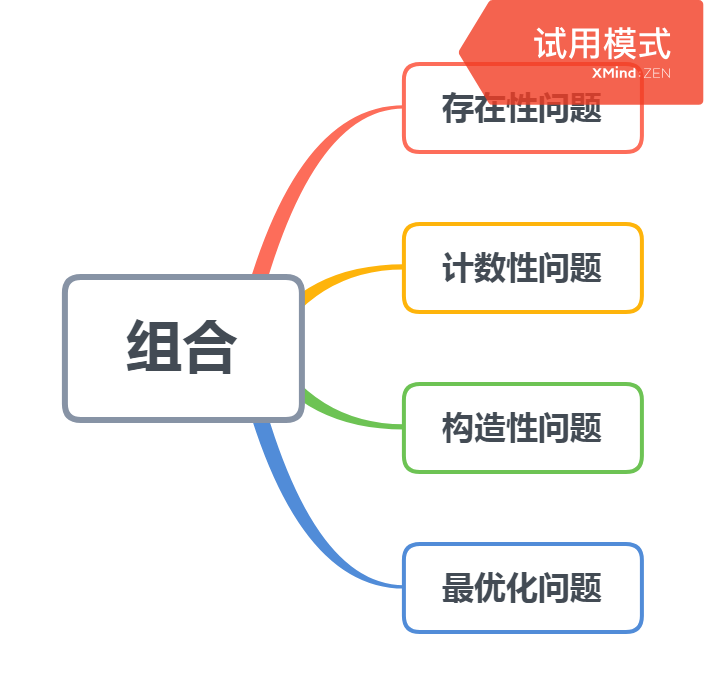
二、组合类问题
存在性问题
计数性问题
构造性问题
最优化问题
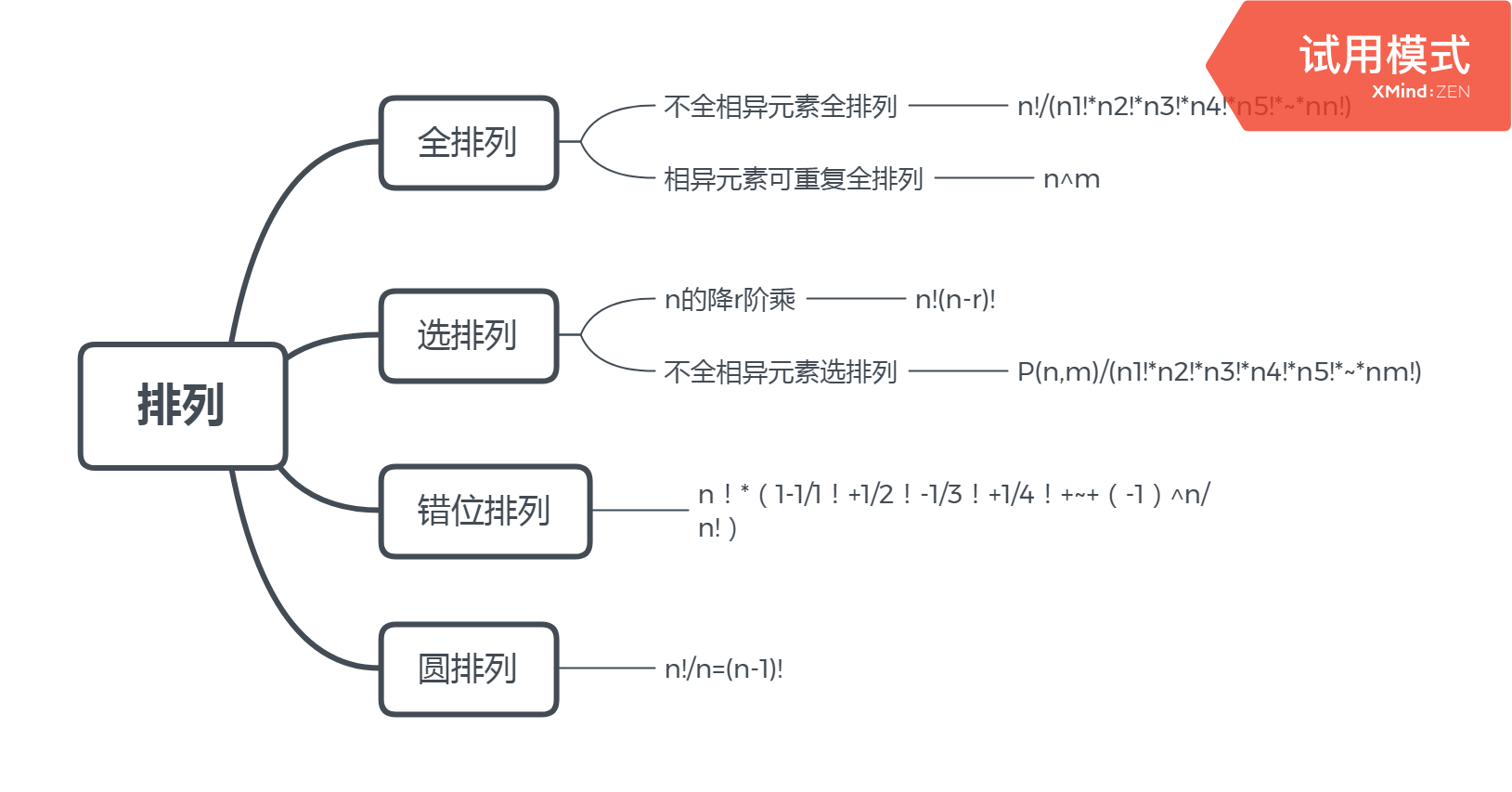
三、排列
全排列
不全相异元素全排列 n!/(n1!*n2!*n3!*n4!*n5!*~*nn!)
相异元素可重复全排列 n^m
选排列
n的降r阶乘 n!(n-r)!
不全相异元素选排列 P(n,m)/(n1!*n2!*n3!*n4!*n5!*~*nm!)
错位排列
n!*(1-1/1!+1/2!-1/3!+1/4!+~+(-1)^n/n!)
圆排列
n!/n=(n-1)!
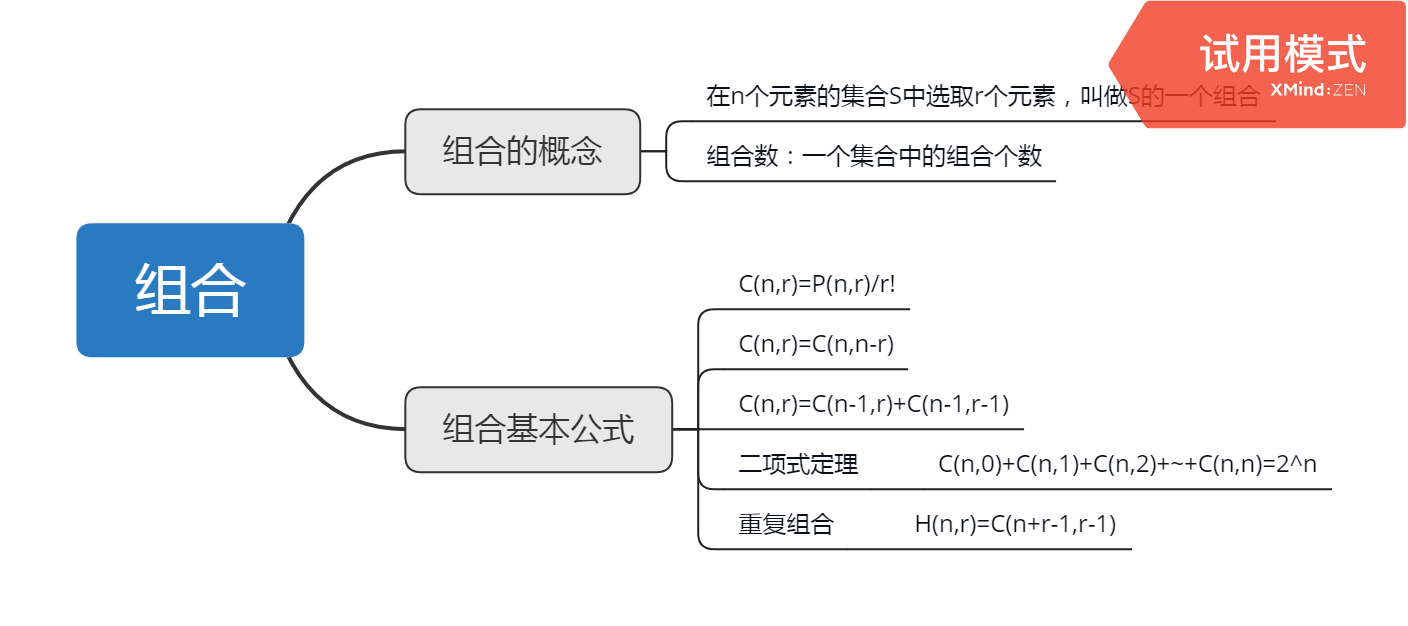
三、组合
组合的概念
在n个元素的集合(互异性)S中选取r个元素,叫做S的一个组合
组合数:一个集合中的组合个数
组合基本公式
C(n,r)=P(n,r)/r!
一个组合进行全排列就是P(n,r)
C(n,r)=C(n,n-r)
在一个集合中选取r个元素有C(n,r)中选择,但我们不是每一次选原来的集合中都剩下了n-r个元素,这些也是组成了一个组合
C(n,r)=C(n-1,r)+C(n-1,r-1)
C(n-1,r)表示现在这个数不选,C(n-1,r-1)表示现在这个数选,所以只需要在前n-1个数中选择r-1个就行,所以C(n,r)就是考虑选择与不选的总和
二项式定理
C(n,0)+C(n,1)+C(n,2)+~+C(n,n)=2^n
简单证明: 将一个长度为n的01串01自由组合的答案就是2^n,对于每一个合法串,1出现总数为x1的就是C(n,x1),所以答案就是1出现的总数p的次数的和
重复组合
H(n,r)=C(n+r-1,n-1)=C(n+r-1,r)
简单证明:假设有n-1个隔板,将r分成了n个部分,那么是不是每一部分就是一个元素选择的次数,总和也就是r



 浙公网安备 33010602011771号
浙公网安备 33010602011771号