Luogu-P2016 战略游戏

 

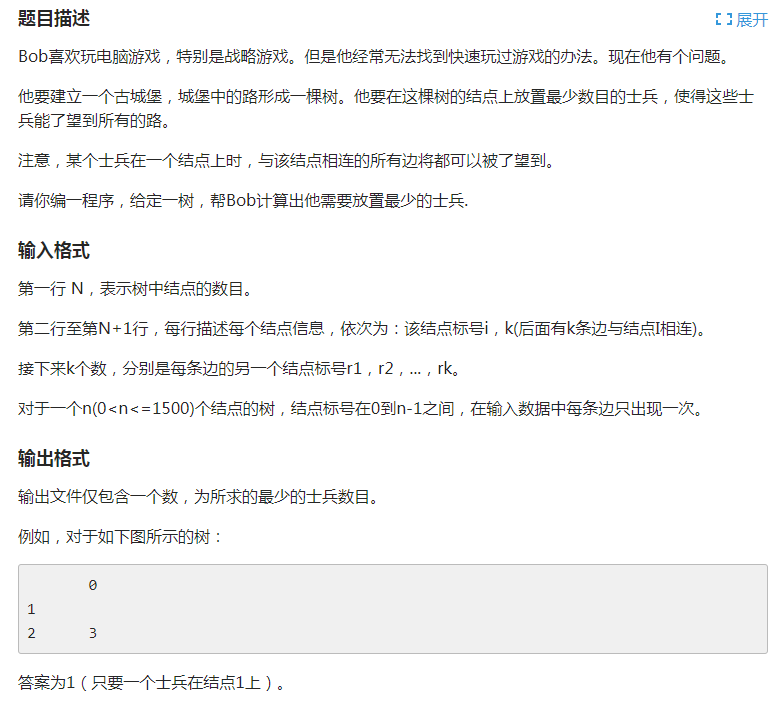
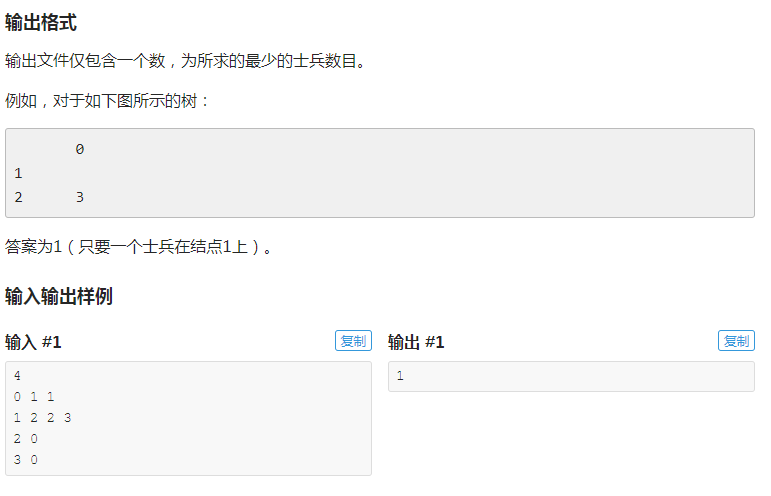
题目

题目链接

 

测试得分：　　100

 

 

主要算法 ：　　树型DP、点的最小覆盖，二分图（匈牙利算法）

 

 

题干：

　　　点的最小覆盖

 

 

应试策略：

1. 定义状态dp[u][0/1]表示u这个节点不放/放士兵

2. 根据题意,如果当前节点不放置士兵,那么它的子节点必须全部放置士兵,因为要满足士兵可以看到所有的边,所以dp[u][0]+=dp[to][1]其中to是u的子节点

3. 如果当前节点放置士兵,它的子节点选不选已经不重要了(因为树形dp自下而上,上面的节点不需要考虑),所以dp[u][1]+=min(dp[to][0],dp[to][1])
   

　　代码

#include<stdio.h>
#include<stdlib.h>
#include<string.h>
#define FORa(i,s,e) for(int i=s;i<=e;i++)
#define FORs(i,s,e) for(int i=s;i>=e;i--)

using namespace std;
const int N=1500,M=1500;
int n,m,root,num_edge,head[N+1],f[N+1][2];
//f[i][0]表示的是在以i为根的子树中，不选i的最小覆盖数,f[i][1]表示的是在以i为根的子树中，选i的最小覆盖数
struct Edge{
    int next,to;
}edge[2*M+2]; 
void Add_edge(int from,int to) {edge[++num_edge]=(Edge){head[from],to},head[from]=num_edge;}
inline int min(int fa,int fb){return fa<fb?fa:fb;}
int Dp(int u,int fa)
{
    f[u][1]=1,f[u][0]=0;//初始化 
    for(int i=head[u];i;i=edge[i].next)
    {
        int v=edge[i].to;
        if(v!=fa) Dp(v,u),f[u][0]+=f[v][1],f[u][1]+=min(f[v][0],f[v][1]);
        //如果u选，则答案是子树最小覆盖和的最小值    
        //如果u不选，则答案是子树选的最小覆盖和的最小值    
    }
}
int main()
{
    int from,to,fcnt;
    scanf("%d",&n);
    memset(f,127,sizeof(f));//初始化 
    FORa(i,1,n)
    {
        scanf("%d%d",&from,&fcnt);
        FORa(j,1,fcnt) scanf("%d",&to),Add_edge(from,to),Add_edge(to,from);
    }
    root=1,Dp(root,-1);
    printf("%d",min(f[root][0],f[root][1]));
    return 0;
}
/*4
0 1 1
1 2 2 3
2 0
3 0*/

总结：

　　1.确定建立模型

　　2.构建知识架构，模型体系