树的中心
一、简介
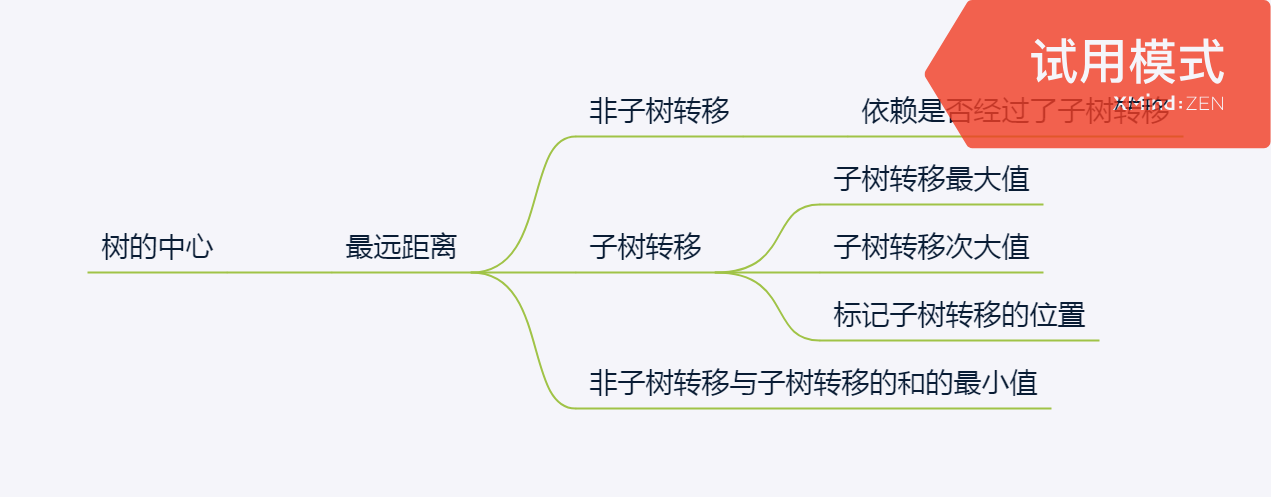
树的中心是指:一个结点,对于每一个点的距离的最大值最小
二、解决
1.Dfs1:标记以结点u为树根的子树链的最大值d1[u],次大值d2[u],以及来源的结点编号c1[u],c2[u]
2.Dfs2:找到链接结点u没有经过u子树的链的最大值fd[u]
如果这个点是前一个节点选中的最大链中的,则这个结点的fd[u]=max(fd[fa[u]],d2[fa[u]])+edge[i].dis;
否则fd[u]=max(fd[fa[u]],d1[fa[u]])+edge[i].dis;
3.最后fd[u]+d1[u]最小的就是答案了
#include<stdio.h> #include<stdlib.h> #define FORa(i,s,e) for(int i=s;i<=e;i++) #define FORs(i,s,e) for(int i=s;i>=e;i--) using namespace std; const int N=1000,INF=2147483647; int n,num_edge,ans=INF,pos,head[N+1],d1[N+1],d2[N+1],c1[N+1],c2[N+1],fd[N+1]; /*d1[u]表示以u为子树的链的最大值,d2[u]表示以u为子树的链的次大值, c1[u]表示以u为子树的链的最大值的子树结点编号,c2[u]表示以u为子树的链的次大值的子树结点编号 fd[u]表示的是结点u以上的不经过u子树的链的最大值 */ struct Edge{ int next,to,dis; }edge[2*N]; inline void Add_edge(int from,int to,int dis) { edge[++num_edge]=(Edge){head[from],to,dis},head[from]=num_edge; } inline int max(int fa,int fb){return fa>fb?fa:fb;} inline int Dfs1(int u,int fa,int dis) { for(int i=head[u];i;i=edge[i].next) { if(edge[i].to!=fa) { Dfs1(edge[i].to,u,dis+edge[i].to); if(d1[edge[i].to]+edge[i].dis>d1[u]) d2[u]=d1[u],d1[u]=d1[edge[i].to]+edge[i].dis,c2[u]=c1[u],c1[u]=edge[i].to; else if(d1[edge[i].to]+edge[i].dis>d2[u]) d2[u]=d1[edge[i].to]+edge[i].dis,c2[u]=edge[i].to; } } //Dfs1找到d1,d2,c1,c2; } inline int Dfs2(int u,int fa) { for(int i=head[u];i;i=edge[i].next) { if(edge[i].to!=fa) { if(c1[fa]!=edge[i].to) fd[edge[i].to]=max(d1[u],fd[u])+edge[i].dis;//u的最大值中不包含最大链 else fd[edge[i].to]=max(d2[u],fd[u])+edge[i].dis;//u的最大值中包含最大链,则用次大链代替 Dfs2(edge[i].to,u); } } } int main() { int from,to,dis; scanf("%d",&n); FORa(i,2,n) { scanf("%d%d%d",&from,&to,&dis); Add_edge(from,to,dis),Add_edge(to,from,dis); } Dfs1(1,0,0); Dfs2(1,0); FORa(i,1,n) if(d1[i]+fd[i]<ans) ans=d1[i]+fd[i],pos=i; printf("%d %d",pos,ans); return 0; } /*8 1 2 4 1 3 2 2 5 1 2 6 4 3 4 9 5 7 10 3 8 10 */



 浙公网安备 33010602011771号
浙公网安备 33010602011771号