ST表

 

一、RMQ问题　　

　　给定一个长度为N的区间，M个询问，每次询问Li到Ri这段区间元素的最大值/最小值。　　

　　如果暴力找最大值，复杂度是o(n)。但如果查询多次，这个复杂度就很大了。

　　解决这个问题的方法是离线ST表和支持在线修改的线段树

二、ST表

　　一种利用dp求解区间最值的倍增算法。

三、定义

　　f[i][j]表示i到i+2^(j−1)这段区间的最大值。

四、预处理

　　f[i][0]=a[i]。即i到i区间的最大值就是a[i]。

五、状态转移

　　将f[i][j]平均分成两段，一段为f[i][j−1]，另一段为f[i+2j−1][j−1]。

　　两段的长度均为2^(j-1)。f[i][j]的最大值即这两段的最大值中的最大值。

　　　　f[i][j]=max(f[i][j−1],f[i+2^(j-1)][j−1])

 六、查询

　　需要查询的区间为[i,j]，则需要找到两个覆盖这个闭区间的最小幂区间。

　　这两个区间可以重复，因为两个区间是否相交对区间最值没有影响。（如下图）

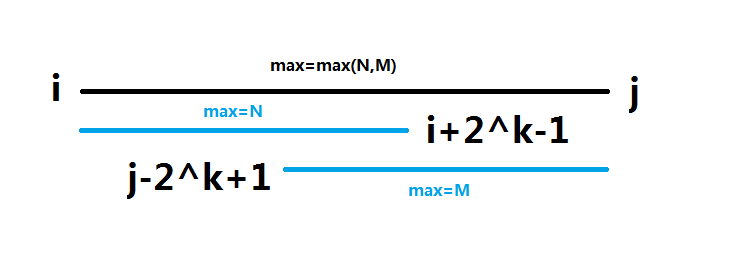
七、代码

#include<stdio.h>
#include<stdlib.h>
#define FORa(i,s,e) for(int i=s;i<=e;i++)
#define FORs(i,s,e) for(int i=s;i>=e;i--)
using namespace std;

const int N=100,M=20000,K=10;
int n,m,a[N+1],f[M+1][K+1],log[K+1];
inline int max(int fa,int fb){return fa>fb?fa:fb;}
int main()
{
    scanf("%d%d",&n,&m);
    log[0]=-1;
    FORa(i,1,K) log[i]=log[i>>1]+1;
    FORa(i,1,n) scanf("%d",&a[i]),f[i][0]=a[i];
    FORa(j,1,K)
        for(int i=1;i+(1<<j)-1<=n;i++)
            f[i][j]=max(f[i][j-1],f[i+(1<<(j-1))][j-1]);
    int x,y;
    while(m--)
    {
        scanf("%d%d",&x,&y);
        int s=log[y-x+1];
        printf("%d\n",max(f[x][s],f[y-(1<<s)+1][s]));
    }
    return 0; 
}

/*10  2 
3 2 4 5 6 8 1 2 9 7
1 4 
3 8*/

 

八、相关转载和推荐文章(十分感谢这些博主)

　　　　【学习笔记】ST表