树链剖分
前言:
首先,在学树链剖分之前最好先把 LCA、树形DP、DFS序 这三个知识点学了
emm还有必备的 链式前向星、线段树 也要先学了。
如果这三个知识点没掌握好的话,树链剖分难以理解也是当然的。
一、简介
树链剖分 就是对一棵树分成几条链,把树形变为线性,减少处理难度
需要处理的问题:
-
- 将树从x到y结点最短路径上所有节点的值都加上z
- 求树从x到y结点最短路径上所有节点的值之和
- 将以x为根节点的子树内所有节点值都加上z
- 求以x为根节点的子树内所有节点值之和
概念
-
- 重儿子:对于每一个非叶子节点,它的儿子中 以那个儿子为根的子树节点数最大的儿子 为该节点的重儿子 (Ps: 感谢@shzr大佬指出我此句话的表达不严谨qwq, 已修改)
- 轻儿子:对于每一个非叶子节点,它的儿子中 非重儿子 的剩下所有儿子即为轻儿子
- 叶子节点没有重儿子也没有轻儿子(因为它没有儿子。。)
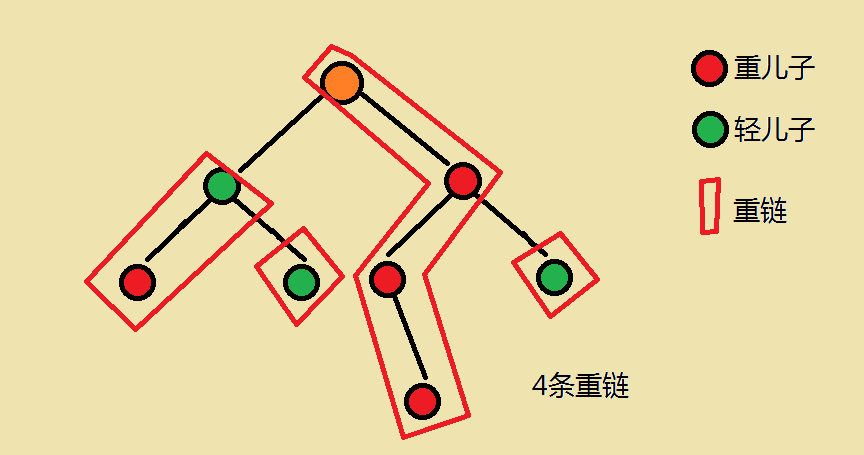
- 重边:一个父亲连接他的重儿子的边称为重边 //原写法:连接任意两个重儿子的边叫做重边
- 轻边:剩下的即为轻边
- 重链:相邻重边连起来的 连接一条重儿子 的链叫重链
- 对于叶子节点,若其为轻儿子,则有一条以自己为起点的长度为1的链
- 每一条重链以轻儿子为起点
性质
如果边(u,v)为轻边,那么,size(u)>=size(v)*2
根到某一节点经过的路径中轻边的数量一定不多于log(n)
根到某一节点经过的路径中重链的数量一定不多于log(n)
二、算法流程
dfs1()
这个dfs1要处理几件事情:
-
- 标记每个点的深度deep[]
- 标记每个点的父亲fa[]
- 标记每个非叶子节点的子树大小(含它自己)
- 标记每个非叶子节点的重儿子编号w_son[]
-
inline void Dfs1(int u,int father,int fdeep) { deep[u]=fdeep,fa[u]=father,root_size[u]=1;//标记节点的父亲,深度,当前以u为树根的树中的节点个数 int pw_son=-1;//先设重儿子的root_size为-1 for(int i=head[u];i;i=edge[i].next) { if(edge[i].to==father) continue;//无向图"返祖边"不需要 Dfs1(edge[i].to,u,fdeep+1);//搜索儿子节点 if(root_size[edge[i].to]>pw_son) w_son[u]=edge[i].to; root_size[u]+=root_size[edge[i].to];//更新重儿子 } }
dfs2()
这个dfs2也要预处理几件事情
-
- 标记每个点的新编号id
- 赋值每个点的初始值到新编号上
- 处理每个点所在链的顶端
- 处理每条链
-
inline void Dfs2(int u,int ftop) { top[u]=ftop;//将u加入链头为ftop的链中 id[u]=++cnt;//记录每一个节点的时间戳 w[cnt]=a[u];//按照时间戳加入权值 if(!son[u]) return;//没有儿子,直接返回 Dfs2(son[u],ftop);//先深搜重儿子,这样就会保证重儿子的序列尽可能的小 for(int i=haed[u];i;i=edge[i].next) if(edge[i].to!=u&&edge[i].to!=son[u]) Dfs2(edge[i].to,edge[i].to)//生成一条以edge[i].to为链头的新链 }
效果图如下图所示(有点小lazy)

对于下面例题中的模板的处理的问题
-
- 处理任意两点间路径上的点权和
- 处理一点及其子树的点权和
- 修改任意两点间路径上的点权
- 修改一点及其子树的点权
线段树构造
inline void Build_st(int k,int l,int r) { if(l==r) { sum[k]=w[l]; return; } int mid=(l+r)>>1; Build_st(k<<1,l,mid),Build_st(k<<1|1,mid+1,r); sum[k]=sum[k<<1]+sum[k<<1|1]; }
线段树修改
inline void Modify_st(int k,int l,int r) { if(modify_x>r||modify_y<l) return; if(l>=modify_x&&r<=modify_y) {add[k]+=modify_v;return;} sum[k]+=modify_v*(min(modify_y,r)-max(modify_x,l)+1); int mid=(l+r)>>1; if(modify_x<=mid) Modify_st(k<<1,l,mid); if(modify_y>mid) Modify_st(k<<1|1,mid+1,r); }
线段树询问
inline int Query_st(int k,int l,int r) { if(query_x>r||query_y<l) return 0; if(l>=query_x&&r<=query_y) return (sum[k]+add[k]*(r-l+1))%mod; int res=(min(r,query_y)-max(query_x,l)+1)*add[k]%mod,mid=(l+r)>>1; if(query_x<=mid) res=(res+Query_st(k<<1,l,mid))%mod; if(query_y>mid) res=(res+Query_st(k<<1|1,mid+1,r))%mod; return res%mod; }
修改任意两点间路径上的点权
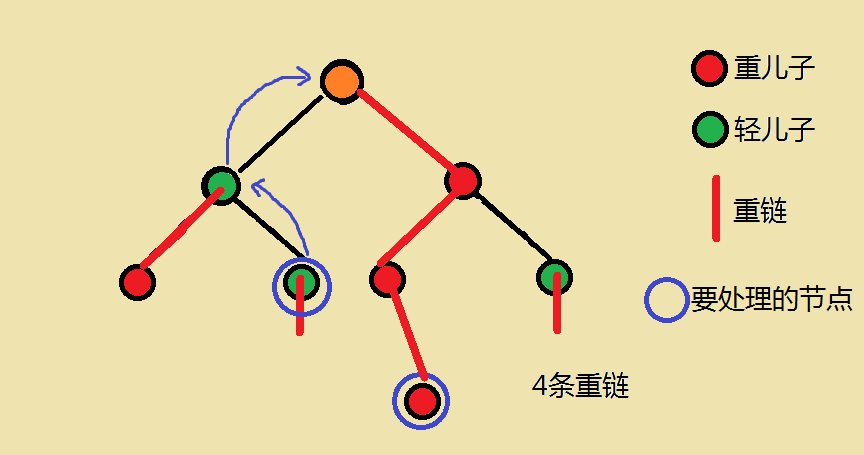
设所在链顶端的深度更深的那个点为x点
-
- ans加上x点到x所在链顶端 这一段区间的点权和
- 把x跳到x所在链顶端的那个点的上面一个点
不停执行这两个步骤,直到两个点处于一条链上,这时再加上此时两个点的区间和即可
inline void Modify_path(int x,int y,int v) { v=v%mod; while(top[x]!=top[y])//当x,y没有在同一条链上,循环跳动 { if(deep[top[x]]<deep[top[y]]) Swap(x,y);//先处理链头深度最浅的 modify_x=id[top[x]],modify_y=id[x],modify_v=v;//修改链头到现在的值 Modify_st(1,1,n); x=fa[top[x]];//将x跳到链头上的一个新的链中 } if(deep[x]>deep[y]) Swap(x,y);//因为此时x与y已经在同一条链中,修改操作将x的深度跳到最小,这样有利于在线段树中操作修改 modify_x=id[x],modify_y=id[y],modify_v=v; Modify_st(1,1,n); }
处理任意两点间路径上的点权和
inline int Query_path(int x,int y) { int res=0; while(top[x]!=top[y])//当x,y没有在同一条链上,循环跳动 { if(deep[top[x]]<deep[top[y]]) Swap(x,y);//先处理链头深度最深的 query_x=id[top[x]],query_y=id[x]; res=(res+Query_st(1,1,n))%mod;//累加链头到现在的值 x=fa[top[x]];//将x跳到链头上的一个新的链中 } if(deep[x]>deep[y]) Swap(x,y); query_x=id[x],query_y=id[y]; res=(res+Query_st(1,1,n))%mod; return res;//因为此时x与y已经在同一条链中,修改操作将x的深度跳到最小,这样有利于在线段树中操作累加 }
修改一点及其子树的点权
想到记录了每个非叶子节点的子树大小(含它自己),并且每个子树的新编号都是连续的于是直接线段树区间查询即可时间复杂度为O(logn)
inline void Modify_subtree(int x,int v) { v=v%mod; modify_x=id[x],modify_y=id[x]+root_size[x]-1,modify_v=v; Modify_st(1,1,n);//包含x的子树的在线段树上标号是连续的直接修改 }
处理一点及其子树的点权和
inline int Query_subtree(int x) { query_x=id[x],query_y=id[x]+root_size[x]-1; return Query_st(1,1,n);//包含x的子树的在线段树上标号是连续的直接累加 }
完整代码
#include<stdio.h> #include<stdlib.h> #define LL long long #define FORa(i,s,e) for(int i=s;i<=e;i++) #define FORs(i,s,e) for(int i=s;i>=e;i--) using namespace std; const int N=1e6,M=1e6; int n,num_operating,root,mod,t_s; int num_edge,head[N+1]; int a[N+1],deep[N+1],fa[N+1],w_son[N+1],root_size[N+1]; int top[N+1],id[N+1],w[4*N+4]; /* t_s,表示的是时间戳 deep[u]代表的是节点u的深度,fa[u]代表的是节点u的父亲,w_son[u]代表的节点u的重儿子,root_size[u]表示的是以u为树根的树中的节点个数 top[u]表示的是u所在链上的深度最小的点,就是我们说的链头,id[u]表示的是节点u的时间戳(编号),w[i]代表的是节点编号为i的点权值 */ struct Edge{ int next,to; }edge[2*M+2]; inline void Add_edge(int from,int to){edge[++num_edge]=(Edge){head[from],to},head[from]=num_edge;} inline void Swap(int &fa,int &fb){int t=fa;fa=fb;fb=t;} inline int max(int fa,int fb){return fa>fb?fa:fb;} inline int min(int fa,int fb){return fa<fb?fa:fb;} //线段树基本讲解 https://www.cnblogs.com/SeanOcean/p/11286568.html 此处省略讲解 int query_x,query_y,query_u,modify_x,modify_y,modify_v; LL add[N+1],sum[N+1]; inline void Build_st(int k,int l,int r) { if(l==r) { sum[k]=w[l]; return; } int mid=(l+r)>>1; Build_st(k<<1,l,mid),Build_st(k<<1|1,mid+1,r); sum[k]=sum[k<<1]+sum[k<<1|1]; } inline void Modify_st(int k,int l,int r) { if(modify_x>r||modify_y<l) return; if(l>=modify_x&&r<=modify_y) {add[k]+=modify_v;return;} sum[k]+=modify_v*(min(modify_y,r)-max(modify_x,l)+1); int mid=(l+r)>>1; if(modify_x<=mid) Modify_st(k<<1,l,mid); if(modify_y>mid) Modify_st(k<<1|1,mid+1,r); } inline int Query_st(int k,int l,int r) { if(query_x>r||query_y<l) return 0; if(l>=query_x&&r<=query_y) return (sum[k]+add[k]*(r-l+1))%mod; int res=(min(r,query_y)-max(query_x,l)+1)*add[k]%mod,mid=(l+r)>>1; if(query_x<=mid) res=(res+Query_st(k<<1,l,mid))%mod; if(query_y>mid) res=(res+Query_st(k<<1|1,mid+1,r))%mod; return res%mod; } inline void Modify_subtree(int x,int v) { v=v%mod; modify_x=id[x],modify_y=id[x]+root_size[x]-1,modify_v=v; Modify_st(1,1,n);//包含x的子树的在线段树上标号是连续的直接修改 } inline int Query_subtree(int x) { query_x=id[x],query_y=id[x]+root_size[x]-1; return Query_st(1,1,n);//包含x的子树的在线段树上标号是连续的直接累加 } inline void Modify_path(int x,int y,int v) { v=v%mod; while(top[x]!=top[y])//当x,y没有在同一条链上,循环跳动 { if(deep[top[x]]<deep[top[y]]) Swap(x,y);//先处理链头深度最浅的 modify_x=id[top[x]],modify_y=id[x],modify_v=v;//修改链头到现在的值 Modify_st(1,1,n); x=fa[top[x]];//将x跳到链头上的一个新的链中 } if(deep[x]>deep[y]) Swap(x,y);//因为此时x与y已经在同一条链中,修改操作将x的深度跳到最小,这样有利于在线段树中操作修改 modify_x=id[x],modify_y=id[y],modify_v=v; Modify_st(1,1,n); } inline int Query_path(int x,int y) { int res=0; while(top[x]!=top[y])//当x,y没有在同一条链上,循环跳动 { if(deep[top[x]]<deep[top[y]]) Swap(x,y);//先处理链头深度最浅的 query_x=id[top[x]],query_y=id[x]; res=(res+Query_st(1,1,n))%mod;//累加链头到现在的值 x=fa[top[x]];//将x跳到链头上的一个新的链中 } if(deep[x]>deep[y]) Swap(x,y); query_x=id[x],query_y=id[y]; res=(res+Query_st(1,1,n))%mod; return res;//因为此时x与y已经在同一条链中,修改操作将x的深度跳到最小,这样有利于在线段树中操作累加 } inline void Dfs1(int u,int father,int fdeep) { deep[u]=fdeep,fa[u]=father,root_size[u]=1;//标记节点的父亲,深度,当前以u为树根的树中的节点个数 int pw_son=0;//先设重儿子的root_size为-1 for(int i=head[u];i;i=edge[i].next) { if(edge[i].to==father) continue;//无向图"返祖边"不需要 Dfs1(edge[i].to,u,fdeep+1);//搜索儿子节点 if(root_size[edge[i].to]>pw_son) w_son[u]=edge[i].to,pw_son=root_size[edge[i].to]; root_size[u]+=root_size[edge[i].to];//更新重儿子 } } inline void Dfs2(int u,int ftop) { top[u]=ftop;//将u加入链头为ftop的链中 id[u]=++t_s;//记录每一个节点的时间戳 w[t_s]=a[u]%mod;//按照时间戳加入权值 if(!w_son[u]) return;//没有儿子,直接返回 Dfs2(w_son[u],ftop);//先深搜重儿子,这样就会保证重儿子的序列尽可能的小 for(int i=head[u];i;i=edge[i].next) if(edge[i].to!=fa[u]&&edge[i].to!=w_son[u]) Dfs2(edge[i].to,edge[i].to);//生成一条以edge[i].to为链头的新链 } int main() { int from,to,operating,x,y,v; scanf("%d%d%d%d",&n,&num_operating,&root,&mod); FORa(i,1,n) scanf("%d",&a[i]); FORa(i,2,n) { scanf("%d%d",&from,&to); Add_edge(from,to),Add_edge(to,from); } Dfs1(root,0,1); Dfs2(root,root); Build_st(1,1,n); FORa(i,1,num_operating) { scanf("%d",&operating); if(operating==1) scanf("%d%d%d",&x,&y,&v),Modify_path(x,y,v); else if(operating==2) scanf("%d%d",&x,&y),printf("%d\n",Query_path(x,y)); else if(operating==3) scanf("%d%d",&x,&v),Modify_subtree(x,v); else scanf("%d",&x),printf("%d\n",Query_subtree(x)); } return 0; } /*5 5 2 24 7 3 7 8 0 1 2 1 5 3 1 4 1 3 4 2 3 2 2 4 5 1 5 1 3 2 1 3*/
三、例题
四、相关转载于推荐文章(十分感谢这些博主)



 浙公网安备 33010602011771号
浙公网安备 33010602011771号