线段树
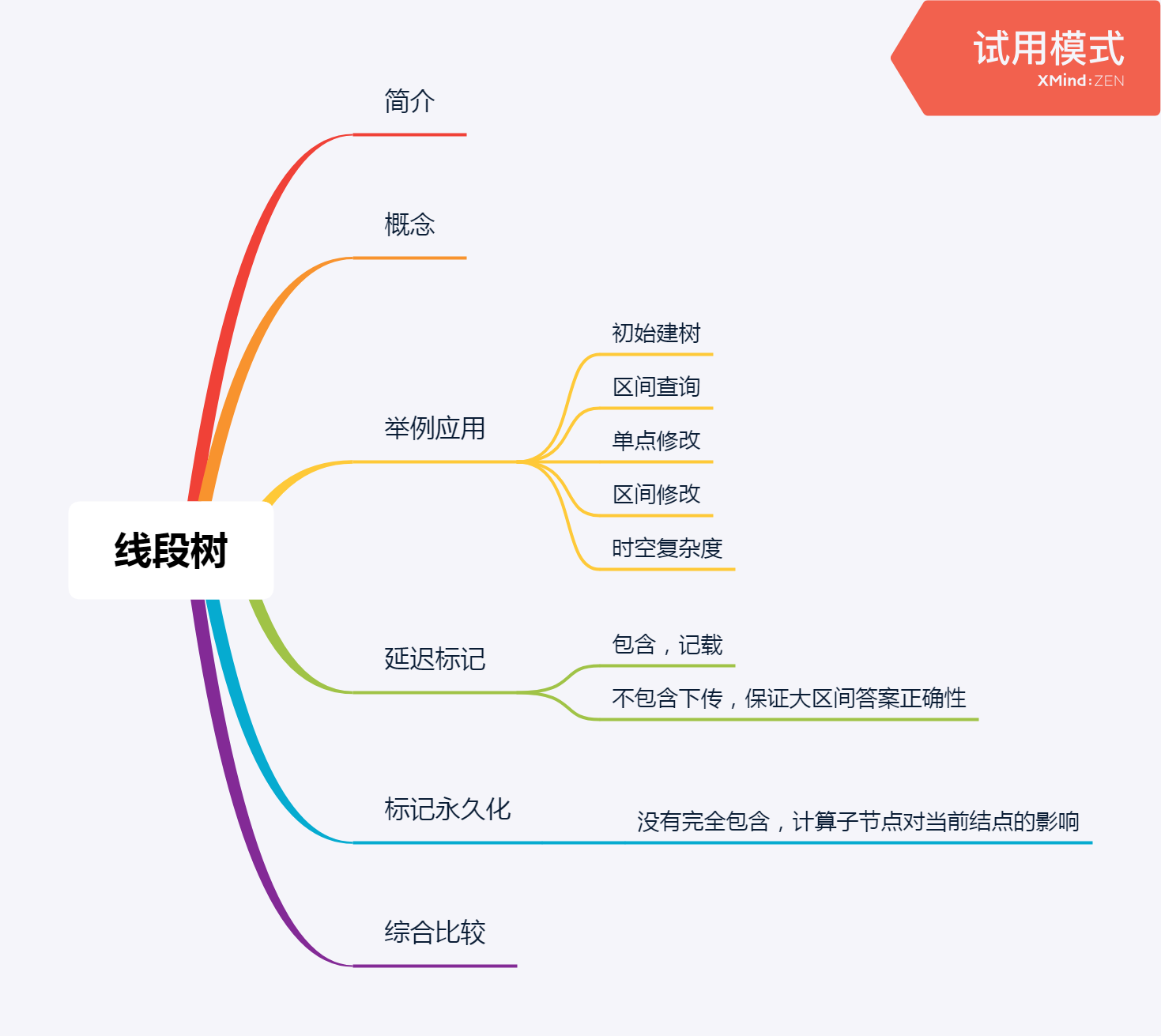
一、简介
对于线段树中的每一个非叶子节点[a,b],它的左儿子表示的区间为[a,(a+b)/2],右儿子表示的区间为[(a+b)/2+1,b]。因此线段树是平衡二叉树,最后的子节点数目为N,即整个线段区间的长度。
使用线段树可以快速的查找某一个节点在若干条线段中出现的次数,时间复杂度为O(logN)。而未优化的空间复杂度为2N,实际应用时一般还要开4N的数组以免越界,因此有时需要离散化让空间压缩。
二、概念
将[1,n]分解成若干特定的子区间(数量不超过4*n)
用线段树对“编号连续”的一些点,进行修改或者统计操作,修改和统计的复杂度都是O(log2(n))
用线段树统计的东西,必须符合区间加法,(也就是说,如果已知左右两子树的全部信息,比如要能够推出父节点);否则,不可能通过分成的子区间来得到[L,R]的统计结果。
一个问题,只要能化成对一些“连续点”的修改和统计问题,基本就可以用线段树来解决了
三、应用
1.初始建树
void Build(int k,int l,int r) { if(l==r){mi[k]=a[l];return;}//达到叶子结点,直接返回叶子结点的信息 int mid=(l+r)>>1; Build(k<<1,l,mid),Build(k<<1|1,mid+1,r);//搜索左右子树 mi[k]=min(mi[k<<1],mi[k<<1|1]);//左右子树信息汇总上传 }
2.区间查询操作
int Query(int k,int l,int r) { if(query_x>r||query_y<l) return INF;//没有包含目标区间 if(l>=query_x&&r<=query_y) return mi[k];//目标区间包含此区间,直接返回信息 int mid=(l+r)>>1; return min(Query(k<<1,l,mid),Query(k<<1|1,mid+1,r));//返回当前子区间构成的类目标区间的信息 }
3.单点修改操作
void Change(int k,int l,int r) { if(change_x>r||change_x<l) return;//不在范围之中,直接结束 if(l==r&&l==change_x) {mi[k]=change_v;return;}//如果已经到了叶子结点了,直接修改叶子节点的信息,接着返回 int mid=(l+r)>>1; Change(k<<1,l,mid),Change(k<<1|1,mid+1,r);//在左右子树中寻找目标节点修改 mi[k]=min(mi[k<<1],mi[k<<1|1]);//改变后的信息汇总 }
4.区间修改
四、时空复杂度
单点修改 O(logn)
区间修改 O(logn)
单点查询 O(logn)
区间查询 O(logn)
五、延迟标记
标记累加
void Add(int k,int l,int r,int add_v) { add[k]+=add_v;//标记更新 sum[k]+=(r-l+1)*add_v;//修改值 }
标记下放
void Pushdown(int k,int l,int r) { if(!add[k]) return; int mid=(l+r)>>1; Add(k<<1,l,mid,add[k]),Add(k<<1|1,mid+1,r,add[k]);//标记下放 add[k]=0;//删除已经下放的标记 }
区间修改
void Modify(int k,int l,int r) { if(modify_y<l||modify_x>r) return;//目标区间于此区间没有交集,结束 if(l>=modify_x&&r<=modify_y) return Add(k,l,r,add0);//此区间完全包含在目标区间中,打标记 Pushdown(k,l,r);//如果没有完全包含,只是局部包含的的话,标记下放 int mid=(l+r)>>1; if(modify_x<=mid) Modify(k<<1,l,mid);//拆分修改两个子区间 if(modify_y>mid) Modify(k<<1|1,mid+1,r); sum[k]=sum[k<<1]+sum[k<<1|1];//汇总更新区间 }
区间查询
int Query(int k,int l,int r) { if(query_x>r||query_y<l) return 0;//与目标区间无交集,直接返回 if(l>=query_x&&r<=query_y) return sum[k];//此区间完全包含在目标区间中,直接返回 Pushdown(k,l,r);//如果没有完全包含,只是局部包含的的话,标记下放 int mid=(l+r)>>1,res=0; if(query_x<=mid) res=Query(k<<1,l,mid);//拆分修改两个子区间 if(query_y>mid) res+=Query(k<<1|1,mid+1,r);//汇总更新区间 return res; }
源代码
#include<stdio.h> #include<stdlib.h> #define FORa(i,s,e) for(int i=s;i<=e;i++) #define FORs(i,s,e) for(int i=s;i>=e;i--) using namespace std; const int N=100; int add[4*N+4],sum[4*N+4]; int modify_x,modify_y,query_x,query_y,add0; int p,n,m; void Add(int k,int l,int r,int add_v) { add[k]+=add_v;//标记更新 sum[k]+=(r-l+1)*add_v;//修改值 } void Pushdown(int k,int l,int r) { if(!add[k]) return; int mid=(l+r)>>1; Add(k<<1,l,mid,add[k]),Add(k<<1|1,mid+1,r,add[k]);//标记下放 add[k]=0;//删除已经下放的标记 } void Modify(int k,int l,int r) { if(modify_y<l||modify_x>r) return;//目标区间于此区间没有交集,结束 if(l>=modify_x&&r<=modify_y) return Add(k,l,r,add0);//此区间完全包含在目标区间中,打标记 Pushdown(k,l,r);//如果没有完全包含,只是局部包含的的话,标记下放 int mid=(l+r)>>1; if(modify_x<=mid) Modify(k<<1,l,mid);//拆分修改两个子区间 if(modify_y>mid) Modify(k<<1|1,mid+1,r); sum[k]=sum[k<<1]+sum[k<<1|1];//汇总更新区间 } int Query(int k,int l,int r) { if(query_x>r||query_y<l) return 0;//与目标区间无交集,直接返回 if(l>=query_x&&r<=query_y) return sum[k];//此区间完全包含在目标区间中,直接返回 Pushdown(k,l,r);//如果没有完全包含,只是局部包含的的话,标记下放 int mid=(l+r)>>1,res=0; if(query_x<=mid) res=Query(k<<1,l,mid);//拆分修改两个子区间 if(query_y>mid) res+=Query(k<<1|1,mid+1,r);//汇总更新区间 return res; } int main() { scanf("%d%d",&n,&m); FORa(i,1,n) { scanf("%d",&add0); modify_x=i,modify_y=i; Modify(1,1,n); } FORa(i,1,m) { scanf("%d",&p); if(p==1) { scanf("%d%d%d",&modify_x,&modify_y,&add0); Modify(1,1,n); } else { scanf("%d%d",&query_x,&query_y); printf("%d\n",Query(1,1,n)); } } return 0; }
六、标记永久化
区间修改
void Modify(int k,int l,int r) { if(modify_y<l||modify_x>r) return;//目标区间于此区间没有交集,结束 if(l>=modify_x&&r<=modify_y) { add[k]+=add0; return; } //此区间完全包含在目标区间中,打标记 //如果没有完全包含,只是局部包含的的话,计算子节点对当前结点的影响 sum[k]+=(min(r,modify_y)-max(l,modify_x)+1)*add0; int mid=(l+r)>>1; if(modify_x<=mid) Modify(k<<1,l,mid);//更新两个子区间 if(modify_y>mid) Modify(k<<1|1,mid+1,r); }
区间查询
int Query(int k,int l,int r) { if(query_x>r||query_y<l) return 0;//与目标区间无交集,直接返回 if(l>=query_x&&r<=query_y) return sum[k]+add[k]*(r-l+1);//此区间完全包含在目标区间中,直接返回 int mid=(l+r)>>1,res=(min(r,query_y)-max(modify_x,l)+1)*add[k]; if(query_x<=mid) res+=Query(k<<1,l,mid);//拆分修改两个子区间 if(query_y>mid) res+=Query(k<<1|1,mid+1,r);//汇总更新区间 return res; }
代码
#include<stdio.h> #include<stdlib.h> #define FORa(i,s,e) for(int i=s;i<=e;i++) #define FORs(i,s,e) for(int i=s;i>=e;i--) using namespace std; const int N=100; int add[4*N+4],sum[4*N+4]; int modify_x,modify_y,query_x,query_y,add0; int p,n,m; inline int max(int fa,int fb){return fa>fb?fa:fb;} inline int min(int fa,int fb){return fa<fb?fa:fb;} void Modify(int k,int l,int r) { if(modify_y<l||modify_x>r) return;//目标区间于此区间没有交集,结束 if(l>=modify_x&&r<=modify_y) { add[k]+=add0; return; } //此区间完全包含在目标区间中,打标记 //如果没有完全包含,只是局部包含的的话,计算子节点对当前结点的影响 sum[k]+=(min(r,modify_y)-max(l,modify_x)+1)*add0; int mid=(l+r)>>1; if(modify_x<=mid) Modify(k<<1,l,mid);//更新两个子区间 if(modify_y>mid) Modify(k<<1|1,mid+1,r); } int Query(int k,int l,int r) { if(query_x>r||query_y<l) return 0;//与目标区间无交集,直接返回 if(l>=query_x&&r<=query_y) return sum[k]+add[k]*(r-l+1);//此区间完全包含在目标区间中,直接返回 int mid=(l+r)>>1,res=(min(r,query_y)-max(modify_x,l)+1)*add[k]; if(query_x<=mid) res+=Query(k<<1,l,mid);//拆分修改两个子区间 if(query_y>mid) res+=Query(k<<1|1,mid+1,r);//汇总更新区间 return res; } int main() { scanf("%d%d",&n,&m); FORa(i,1,n) { scanf("%d",&add0); modify_x=i,modify_y=i; Modify(1,1,n); } FORa(i,1,m) { scanf("%d",&p); if(p==1) { scanf("%d%d%d",&modify_x,&modify_y,&add0); Modify(1,1,n); } else { scanf("%d%d",&query_x,&query_y); printf("%d\n",Query(1,1,n)); } } return 0; }
七、综合比较
分治思想:预处理的时间复杂度达到O(n),修改操作的时间复杂度为O(logn)
线段树与树状数组:常数较大,处理的数据范围比较小
线段树与平衡树:平衡树支持其他的复杂的操作,比如插入,删除,区间移动等操作,但是常数与编程的难度比线段树高
线段树与分块:理论上分块的时间复杂度是O(sqrt(n))的,线段树的理论时间复杂度为O(log(n)),但是线段树的常数比较大,分块的常数以及空间逗都比线段树要小,实际上两者还是存在着很大的区别
八、相关转载与推荐文章(十分感谢这些博主)



 浙公网安备 33010602011771号
浙公网安备 33010602011771号