最短路

 

 

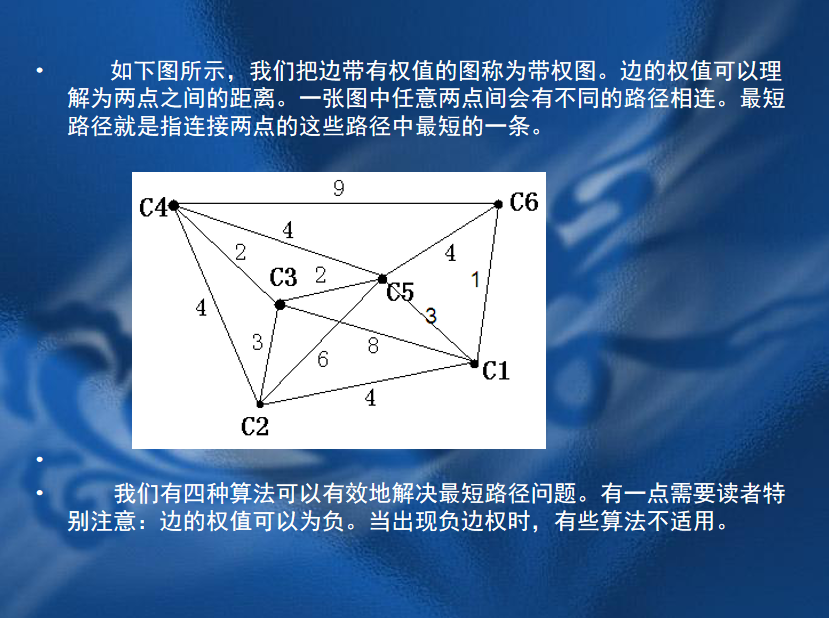
一、Floyd算法和最小环

　　特别详细介绍（此处省略）

 

#include 
    int main()  
    {  
    int e[10][10],k,i,j,n,m,t1,t2,t3;  
    int inf=99999999; //用inf(infinity的缩写)存储一个我们认为的正无穷值
    //读入n和m，n表示顶点个数，m表示边的条数
        scanf("%d %d",&n,&m);  
    //初始化
    for(i=1;i<=n;i++)  
    for(j=1;j<=n;j++)  
    if(i==j) e[i][j]=0;    
    else e[i][j]=inf;  
    //读入边
    for(i=1;i<=m;i++)  
        {  
            scanf("%d %d %d",&t1,&t2,&t3);  
            e[t1][t2]=t3;  
        }  
    //Floyd-Warshall算法核心语句
    for(k=1;k<=n;k++)  
    for(i=1;i<=n;i++)  
    for(j=1;j<=n;j++)  
    if(e[i][j]>e[i][k]+e[k][j] )   
                        e[i][j]=e[i][k]+e[k][j];  
    //输出最终的结果
    for(i=1;i<=n;i++)  
        {  
    for(j=1;j<=n;j++)  
            {  
                printf("%10d",e[i][j]);  
            }  
            printf("\n");  
        }  
    return 0;  
    }

二、Dijkstra算法

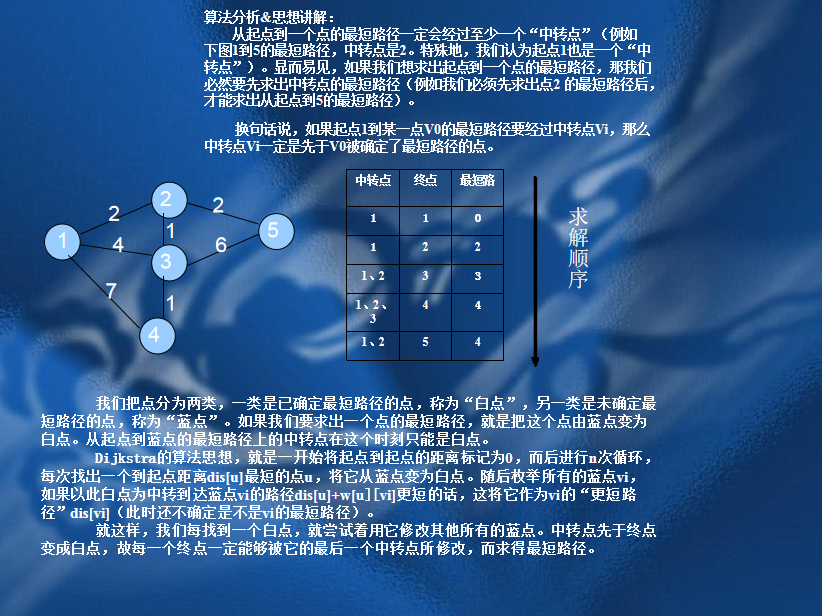
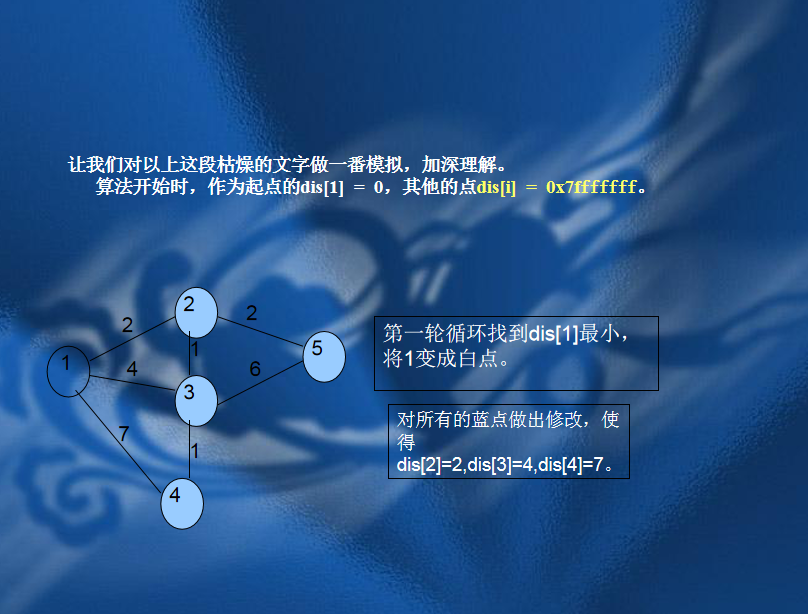
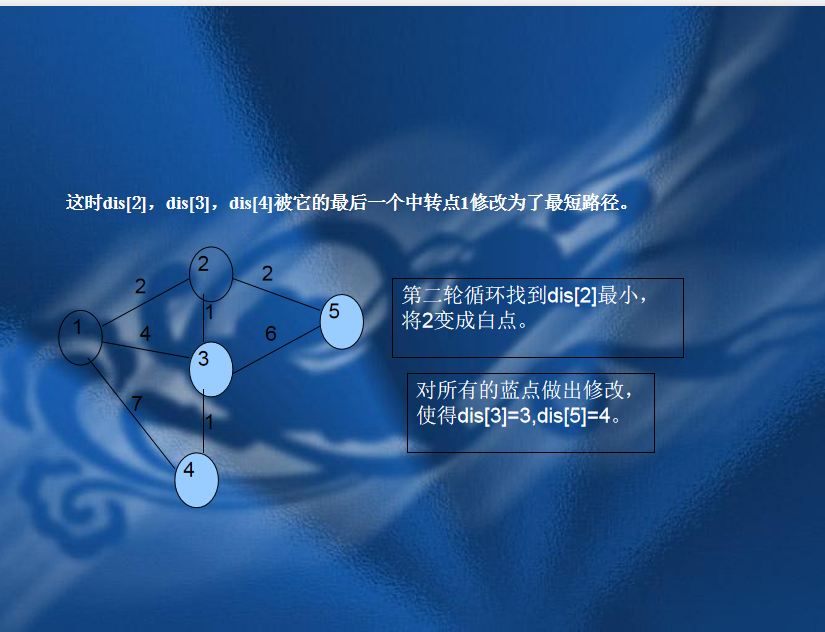
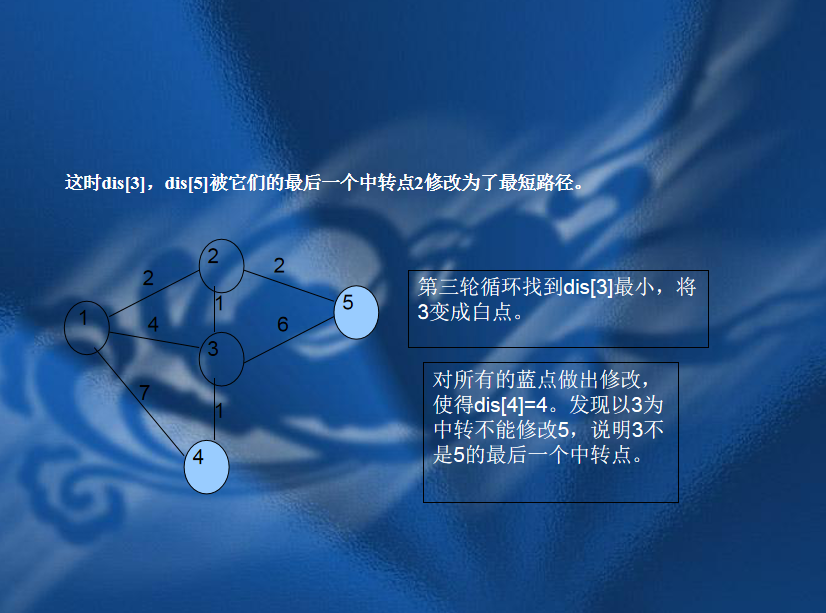
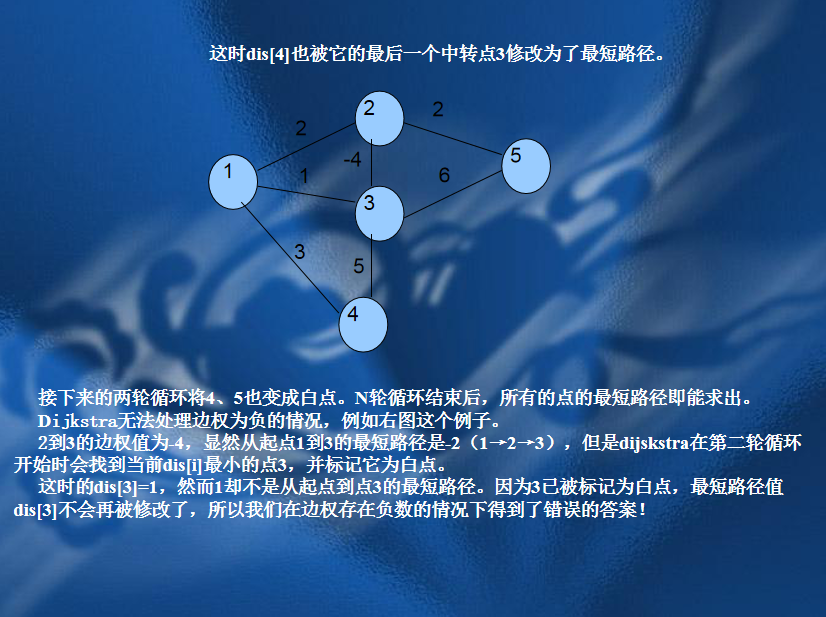
// luogu-judger-enable-o2
#include<queue>
#include<stdio.h>
#include<stdlib.h>
#define INF 2147483647
#define FORa(i,s,e) for(int i=s;i<=e;i++)
#define FORs(i,s,e) for(int i=s;i>=e;i--)
#define gc pa==pb&&(pb=(pa=buf)+fread(buf,1,100000,stdin),pa==pb)?EOF:*pa++
#define File(name) freopen(name".in","r",stdin),freopen(name".out","w",stdout);

using namespace std;
static char buf[100000],*pa=buf,*pb=buf;
inline int read();

const int M=200000,N=100000;
struct Node{
    int next,to,dis;
}edge[M*2];
bool bz[N+1];
int n,m,star,end,dis[N+6],head[N+6],num_edge;
void Add_edge(int from,int to,int d)
{
    num_edge++,edge[num_edge]=(Node){head[from],to,d},head[from]=num_edge;
}
struct Que{
    int u,dis;
    bool operator < (const Que &q) const{ 
        return dis>q.dis;
    } 
}q;
priority_queue<Que> que;
void In()
{
    int from,to,d;
    scanf("%d%d%d",&n,&m,&star);
    FORa(i,1,m) scanf("%d%d%d",&from,&to,&d),Add_edge(from,to,d);
}
void Solve()
{
    FORa(i,1,n) dis[i]=INF;
    dis[star]=0,que.push((Que){star,0});
    while(!que.empty())
    {
        q=que.top(),que.pop();
        if(bz[q.u]) continue;
        bz[q.u]=1;
        for(int i=head[q.u];i;i=edge[i].next)
        {
            if(dis[edge[i].to]>dis[q.u]+edge[i].dis)
            {
                dis[edge[i].to]=dis[q.u]+edge[i].dis;
                if(!bz[edge[i].to]) que.push((Que){edge[i].to,dis[edge[i].to]});
            }
        }
    }
    FORa(i,1,n) printf("%d ",dis[i]);
}
int main()
{
    In();
    Solve();
    return 0;
}

inline int read()
{
    register int x(0);register int f(1);register char c(gc);
    while(c<'0'||c>'9') f=c=='-'?-1:1,c=gc;
    while(c>='0'&&c<='9') x=(x<<1)+ (x<<3)+(c^48),c=gc;
    return x*f;
}

 

三、Bellman-Ford算法

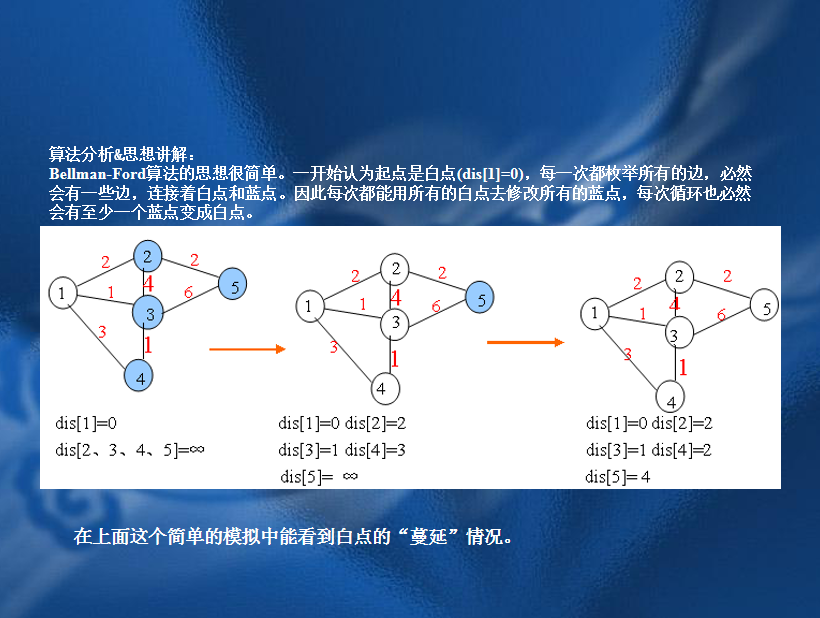
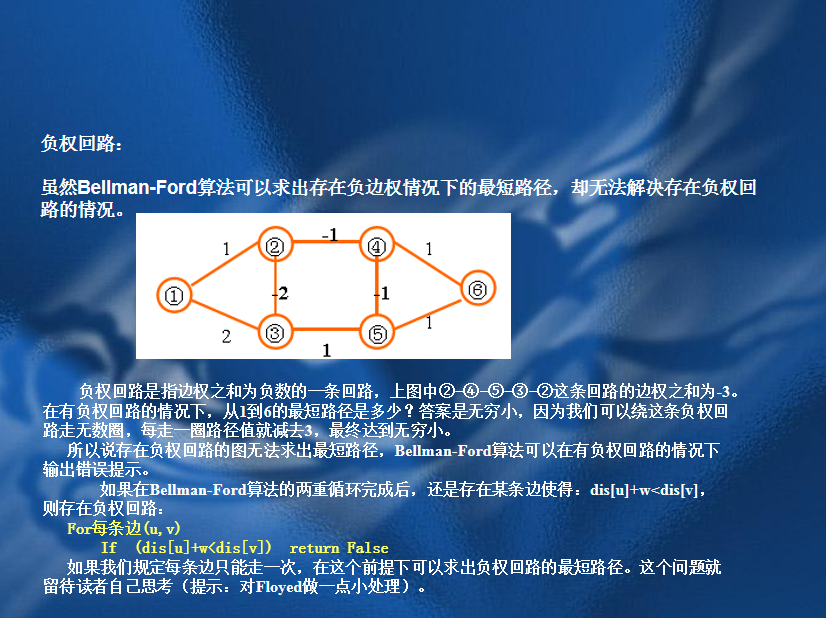
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cmath>
#include<queue>
#include<stack>
#include<map>
#include<sstream>
using namespace std;
typedef long long ll;
const int maxn = 1000 + 10;
const int INF = 1 << 25;
int T, n, m, cases;
struct edge
{
    int u, v, w;
};
edge a[maxn];
int path[maxn], d[maxn];
bool Bellman(int v0)
{
    for(int i = 0; i < n; i++)d[i] = INF, path[i] = -1;
    d[v0] = 0;
    for(int i = 0; i < n; i++)//迭代n次，如果第n次还在更新，说明有负环
    {
        bool update = 0;
        for(int j = 0; j < m; j++)
        {
            int x = a[j].u, y = a[j].v;
            //cout<<x<<" "<<y<<" "<<a[j].w<<endl;
            if(d[x] < INF && d[x] + a[j].w < d[y])
            {
                d[y] = d[x] + a[j].w;
                path[y] = x;
                update = 1;
                if(i == n - 1)//说明第n次还在更新
                {
                    return true;//返回真，真的存在负环
                }
            }
        }
        if(!update)break;//如果没更新了，说明已经松弛完毕
    }
    for(int i = 0; i < n; i++)
    {
        if(i == v0)continue;
        printf("从%d到%d距离是：%2d   ", v0, i, d[i]);
        stack<int>q;
        int x = i;
        while(path[x] != -1)
        {
            q.push(x);
            x = path[x];
        }
        cout<<v0;
        while(!q.empty())
        {
            cout<<"->"<<q.top();
            q.pop();
        }
        cout<<endl;
    }
    return false;
}
int main()
{
    cin >> n >> m;
    for(int i = 0; i < m; i++)cin >> a[i].u >> a[i].v >> a[i].w;
    if(Bellman(0))cout<<"存在负环"<<endl;
    else cout<<"不存在负环"<<endl;
    return 0;
}

 

四、SPFA算法

 

 

#include <bits/stdc++.h>
#define inf 0x3f3f3f3f
using namespace std;

const int M=10005;

struct A{
    int y,time,next;
}a[M<<1];

int pre[M],cent=0;//链式前向星数组
int vis[M],ven[M],nums[M];

//SPFS数组，vis记录最短路，ven记录是否在队列，nums记录入队次数

void add(int x,int y,int k)//链式前向星，加入节点
{
    a[cent].y=y, a[cent].time=k, a[cent].next=pre[x];
    pre[x]=cent++;
}

bool SPFA(int s,int n)
{
    queue <int> q;
    memset(vis,inf,sizeof(vis));
    memset(ven,0,sizeof(ven));
    memset(nums,0,sizeof(nums));
    vis[s]=0;//初始化距离
    ven[s]=1,nums[s]++;//标记s节点在队列，队列次数+1
    q.push(s);
    while(!q.empty())
    {
        int x=q.front();
        q.pop();//出队
        ven[x]=0;//标记不在队列
        for(int i=pre[x]; ~i; i=a[i].next)//遍历与x节点连通的点
        {
            int y=a[i].y;
            if(vis[y]>vis[x]+a[i].time)//更新
            {
                vis[y]=vis[x]+a[i].time;
                if(!ven[y])
                //由于更新了节点，所以后续以这个为基础的最短路，也要更新下
                //所以如果在队列就不用加入，不在的话加入更新后续节点
                {
                    q.push(y);
                    ven[y]=1;//标记这个节点在队列中
                    nums[y]++;//记录加入次数
                    if(nums[y]>n)//如果这个点加入超过n次，说明存在负圈，直接返回
                        return false;
                }
            }
        }
    }
    return true;
}

int main()
{
    int n,m,t;
    int b[M],c[M];
    while(cin>>n>>m>>t)
    {
        cent=0;
        memset(pre,-1,sizeof(pre));
        for(int i=0;i<n;i++)
        {
            int x,y,k;
            cin>>x>>y>>k;
            add(x,y,k);
            add(y,x,k);
        }
        for(int i=0;i<m;i++)
        {
            cin>>b[i];
        }
        for(int i=0;i<t;i++)
        {
            cin>>c[i];
        }
        int minn=inf;
        for(int i=0;i<m;i++)//遍历多个找寻最小
        {
            SPFA(b[i],n);
            for(int j=0;j<t;j++)
                minn=min(minn,vis[c[j]]);
        }
        cout<<minn<<endl;
    }