Luogu-P1004 方格取数

 

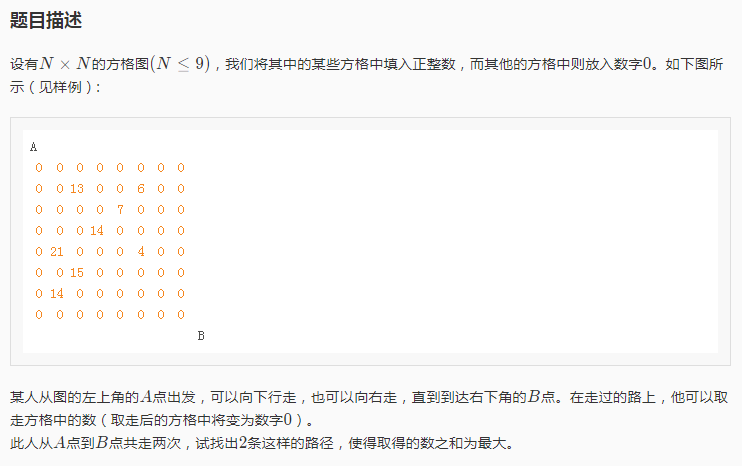
题目

题目链接

 

测试得分：　　100

 

 

主要算法 ：　　动态规划，矩阵DP，压位DP，滚动数组

 

 

 

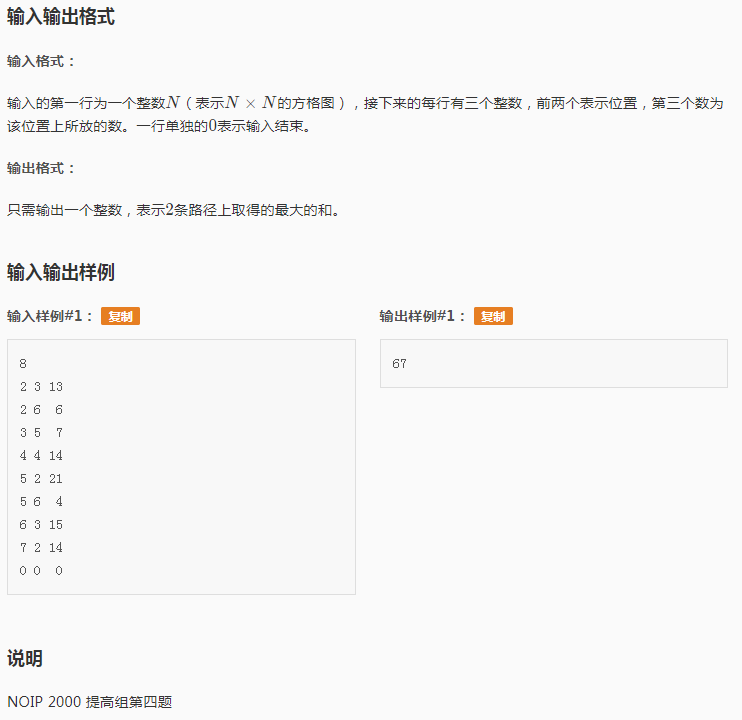
题干：

　　　矩阵DP板子题

 

 

应试策略：

1. 确定算法矩阵路径DP
2. 确定状态a[i][j]记录的是第i行第j列的数值 ，f[i][j][k][l]表示为第一条路到(i,j)，第二条路到(k,l)的两条路径和的最大值
3. 初始值的更改，此题只需要将f数组初始化为最小值0值
4. DP决策与最优化策略=>状态转移方程f[i][j][k][l]=max(max(f[i-1][j][k-1][l-1],f[i][j-1][k-1][l]),max(f[i-1][j][k][l-1],f[i][j-1][k][l]))+a[i][j]+a[k][l];//状态转移：得到四条路的最大值再加上现在的值 ,判断两条路目前有没有相遇，如果相遇，需要减去一个多加的值a[i][j]

　　 代码

 

#include<stdio.h>
#include<stdlib.h>
#define FORa(i,s,e) for(int i=s;i<=e;i++)
#define FORs(i,s,e) for(int i=s;i>=e;i--)

using namespace std;

const int N=9;
int n,a[N+1][N+1],f[N+1][N+1][N+1][N+1];//f[i][j][k][l]表示为第一条路到(i,j)，第二条路到(k,l)的两条路径和的最大值，a[i][j]记录的是第i行第j列的数值 
inline int max(int a,int b) {return a>b?a:b;} 
int main()
{
    int x,y,z;
    scanf("%d%d%d%d",&n,&x,&y,&z);
    while(x&&y)
    {
        a[x][y]=z;
        scanf("%d%d%d",&x,&y,&z);
    }
    FORa(i,1,n)
        FORa(j,1,n)
            FORa(k,1,n)    
                {
                    int l=max(i+j-k,0);
                    f[i][j][k][l]=max(max(f[i-1][j][k-1][l],f[i][j-1][k-1][l]),max(f[i-1][j][k][l-1],f[i][j-1][k][l-1]))+a[i][j]+a[k][l];//状态转移：得到四条路的最大值再加上现在的值 
                    if(i==k&&j==l) f[i][j][k][l]-=a[i][j];//判断两条路目前有没有相遇，如果相遇，需要减去一个多加的值a[i][j] 
                }
    printf("%d",f[n][n][n][n]);
    return 0;
}

 

 

 

 

优化策略：

　　因为移动操作是向下或向左移动的即i+j=k+l,所以确定了i，j，k就可以确定l的值了，l=i+j-k

代码

 

#include<stdio.h>
#include<stdlib.h>
#define FORa(i,s,e) for(int i=s;i<=e;i++)
#define FORs(i,s,e) for(int i=s;i>=e;i--)

using namespace std;

const int N=9;
int n,a[N+1][N+1],f[N+1][N+1][N+1];//a[i][j]记录的是第i行第j列的数值 ，f[i][j][k]表示为第一条路到(i,j)，第二条路到(k,l=i+j-k)的两条路径和的最大值，i+j=k+j,因为移动操作是向下或向左移动的,所以确定了i，j，k就可以确定l的值了
inline int max(int a,int b) {return a>b?a:b;} 
int main()
{
    int x,y,z;
    scanf("%d%d%d%d",&n,&x,&y,&z);
    while(x&&y)
    {
        a[x][y]=z;
        scanf("%d%d%d",&x,&y,&z);
    }
    FORa(i,1,n)
        FORa(j,1,n)
            FORa(k,1,n)    
                {
                    int l=i+j-k;
                    if(l<=0) break;//超出范围退出 
                    f[i][j][k]=max(max(f[i-1][j][k-1],f[i][j-1][k-1]),max(f[i-1][j][k],f[i][j-1][k]))+a[i][j]+a[k][l];//状态转移：得到四条路的最大值再加上现在的值 
                    if(i==k&&j==l) f[i][j][k]-=a[i][j];//判断两条路目前有没有相遇，如果相遇，需要减去一个多加的值a[i][j] 
                }
    printf("%d",f[n][n][n]);
    return 0;
}

 

 

 

 

 

总结：

　　DP尽量向压位，滚动数组方向考虑