Luogu-P1064 金明的预算方案
题目
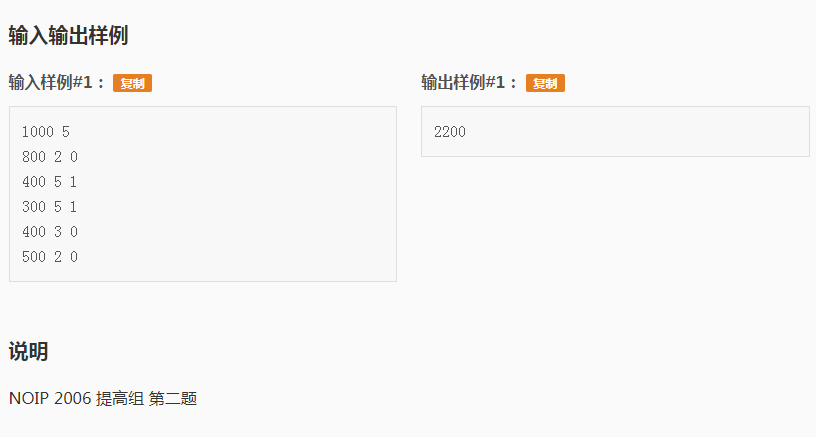
测试得分： 100
主要算法 ： 动态规划，背包，依赖背包（零一背包，分组背包）
题干：
少量附件依赖背包板子
应试策略：
- 第一眼的感觉，搜索搜索很快乐（本蒟蒻很弱，第一眼只能想到搜索），分析完时间复杂度发现，我的天，炸了，果断放弃（其实dalao第一眼就看出了这是附件类型依赖背包的板子题ヾ(ﾟ∀ﾟゞ)）
- 分析完时间复杂度与搜索做法可以向DP背包方向发展，那是什么背包呢（此之前不知道什么是依赖背包ヽ(￣▽￣)ﾉ），由此就想到了正解的方法，但我还是不知道这种背包叫做依赖背包哈！
- 首先将每一个主件的附件都找出来，然后将每一个主件进行分析，将附件当作零一背包处理，将附件的组成结果存起来（结果只包含附件的价值与体积，此时不考虑主件是否加入并且背包都是恰好背包），最后将主件也加入组成分组背包，需要注意的是，主件有一种选择是可以没有附件，只选自己的
- 最后按照分组背包处理，最后在所以允许体积中找到价值最大值
代码
#include<stdio.h> #include<stdlib.h> #include<string.h> #define FORa(i,s,e) for(int i=s;i<=e;i++) #define FORs(i,s,e) for(int i=s;i>=e;i--) using namespace std; const int N=60,V=32000; int v,t,ans,group[N+1],cnt[N+1],f[V+1];//group[i]记录主件i的附件个数，v是最大体积，t是物件个数，ans是最终要输出的答案 ，cnt[i]是主件i这一组可选的组成方案数 struct Node1{ int v,p,q; }a[N+1],son[N][3];//a[]储存输入物品信息，son储存主件的附件信息 struct Node2{ int v,m; }b[N+1][N+1];//最后的主件i这一组可选的组成方案 inline int max(int a,int b){return a>b?a:b;} int main() { scanf("%d%d",&v,&t); FORa(i,1,t) { scanf("%d%d%d",&a[i].v,&a[i].p,&a[i].q); if(a[i].q) son[a[i].q][++group[a[i].q]]=a[i]; } FORa(i,1,t) { if(group[i]) { memset(f,-1,sizeof(f));//考虑要恰好背包 f[0]=0; FORa(l,1,group[i]) FORs(j,v-a[i].v,son[i][l].v) if(f[j]<f[j-son[i][l].v]+son[i][l].v*son[i][l].p&&f[j-son[i][l].v]!=-1)//考虑要恰好背包 f[j]=f[j-son[i][l].v]+son[i][l].v*son[i][l].p; FORa(j,0,v-a[i].v) if(f[j]!=-1) b[i][++cnt[i]].v=j+a[i].v,b[i][cnt[i]].m=f[j]+a[i].p*a[i].v;//组合第i组物品信息 } if(!a[i].q) b[i][++cnt[i]].v=a[i].v,b[i][cnt[i]].m=a[i].v*a[i].p;//只选主件的情况 } memset(f,0,sizeof(f)); FORa(i,1,t) FORs(j,v,0) FORa(k,1,cnt[i]) if(j>=b[i][k].v) f[j]=max(f[j],f[j-b[i][k].v]+b[i][k].m);//像往常处理分组背包一样 FORa(i,0,v) ans=max(ans,f[i]);//寻找最大价值 printf("%d",ans); return 0; }
总结：
状态设计一定需要明确，最好是打备注吧（个人能力太弱的缘故），状态初始量与状态的完全性需特别注意
