线段树
线段树
一、引入
在做题时经常会遇到需要我们维护一个序列的问题，例如给定一个整数序列，每次操作会修改序列某个位置上的数，或是询问你序列中某个区间内所有数的和。考虑到暴力算法，单点修改的复杂度为O(1)，询问区间和的单次复杂度为O(区间长度)，考虑到利用前缀和，询问单次为O(1)，但单点修改为O(区间长度)，但这类问题的m（询问次数）和n（区间长度）往往是105级别的，这两种方法就都不能用了。
线段树就是用来处理在序列上单点修改区间询问（或是区间修改单点询问，甚至是区间修改、区间询问）的问题的一种数据结构。相比于朴素算法O(nm)时间复杂度，线段树能在O(mlogn)的时间复杂度下解决问题。
二、概念
线段树是一棵二叉树，线段树上每个节点对应的是序列的一段区间。如下图所示：
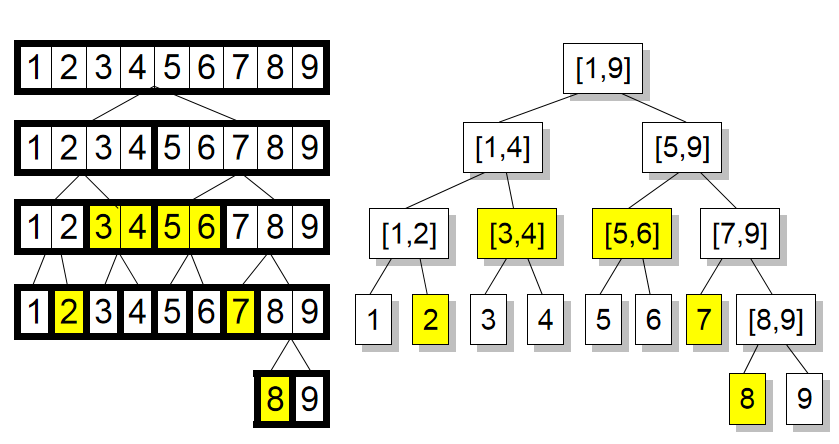
容易发现，根节点对应的是[0,n-1]整个区间。若一个节点对应的区间为[l,r]，当l=r时它是一个叶节点，没有左右儿子；否则它一定有两个儿子，令mid=(l+r)/2，则左儿子对应的区间为[l,mid]，右儿子对应的区间为[mid+1,r]。令线段树的高度（层数）为h，那么不难看出h只有O(logn)级别。
三、使用示例
问题：给定序列a0,a1...an-1，接下来有m次操作，操作有两种，给定i,x将ai修改为x，或是给定l,r，求区间l,r内序列的最小值。
这是线段树的一个最简单的应用。下面以单点修改，区间询问最小值为例，来介绍一下线段树如何工作。
对于线段树，有多种方式，储存方式一般采取左右子树模拟数组储存，具体如下
void Build(LL k,LL l,LL r)
{
if(l==r) {sum[k]=read();return;}
LL mid=l+r>>1;
Build(k<<1,l,mid);建造左子树
Build(k<<1|1,mid+1,r);建造右子树
sum[k]=sum[k<<1]+sum[k<<1|1];子树信息汇总
}
线段树的区间修改Lazy-tag，分两种方式标记下传与标记永久化
*标记下传*
修改操作时我们找到对应的节点，修改add，并且更新节点的sum值。此节点的祖先都能用sum[k]=sum[k*2]+sum[k*2+1]来得到当前修改后正确的区间和。但是子节点的区间和我们无法立即更新。
解决的方案是当我们需要用到这些子节点的信息时再进行更新。就是当我们要从某个节点递归下去时，将当前节点的add值下传，更新两个子节点的add与sum值，并将当前节点的add值清零。
标记
void Add(LL k,LL l,LL r,LL v)
{add[k]+=v,sum[k]+=(r-l+1)*v;}记录现在的影响，将标记累加
下传
void pushdown(LL k,LL l,LL r,LL mid) {
if(add[k]==0) return;
Add(k<<1,l,mid,add[k]); 下传到左右子树
Add(k<<1|1,mid+1,r,add[k]);
add[k]=0;当前树的标记清零
}
修改
void modify(LL k,LL l,LL r,LL x,LL y,LL v) {
if(l>=x&&r<=y) return Add(k,l,r,v);如果在范围内，直接标记修改
LL mid=l+r>>1;
pushdown(k,l,r,mid);标记下传
if(x<=mid) modify(k<<1,l,mid,x,y,v);
if(mid<y) modify(k<<1|1,mid+1,r,x,y,v);
sum[k]=sum[k<<1]+sum[k<<1|1];更新当前树
}
查询
LL query(LL k,LL l,LL r,LL x,LL y) {
if(l>=x&&r<=y) return sum[k];如果在可行范围内直接返回
LL mid=l+r>>1,res=0;
pushdown(k,l,r,mid);下传标记
if(x<=mid) res+=query(k<<1,l,mid,x,y);
if(mid<y) res+=query(k<<1|1,mid+1,r,x,y);
return res;返回左右子树的汇合信息
}
*标记永久化*
修改
void modify(LL k,LL l,LL r,LL x,LL y,LL v) {
if(l>=x&&r<=y) {add[k]+=v;} 记录Lazy-tag
LL mid=l+r>>1;
sum[k]+=(min(y,r)-max(l,x)+1)*v;更新当前的树
if(x<=mid) modify(k<<1,l,mid,x,y,v);
if(mid<y) modify(k<<1|1,mid+1,r,x,y,v);更新左右子树
}
查询
LL query(LL k,LL l,LL r,LL x,LL y) {
if(l>=x&&r<=y) return sum[k]+add[k]*(r-l+1);返回值
LL mid=l+r>>1,res;
res=(min(y,r)-max(l,x)+1)*add[k];记录Lazy-tag影响
if(x<=mid) res+=query(k<<1,l,mid,x,y);
if(mid<y) res+=query(k<<1|1,mid+1,r,x,y);
return res;
}
【总结】：
标记下传
- 标记下传的时候一定要注意Add的细微剪枝，只有Add为0的时候才下传
- 建树的时候一定要注意将数组开到四倍，如果有能力可以将数组开到两倍
- 建子树后不能忘记将子树的值汇总到大树中去
- 标记下传返回的永远是不带add值的，为什么？因为在标记下传的时候，sum值会发生改变，修改时，如果发现已在线段树的某一规定区间内，就立马进行add操作，否则先将原本这棵树标记下传到子树中，更行子树再来更新当前的大树
标记永久化
- 标记永久化时，只需要修改与查询
- 修改的时候，如果发现已在线段树的某一规定区间内，就立马进行add[k]+=v操作，将这颗大树加上应该加的(min(y,r)-max(x,l))*v，再更新子树，将子树加上应有的值
- 查询的时候，如果发现已在线段树的某一规定区间内，就立马进行sum[k]+add[k]*add[k]操作，否则本线段树的add加上子树值
感谢各位与信奥一本通的鼎力相助！
