递归

递归

前面已经介绍了关于递归调用这样一种操作，而递归程序设计是C++语言程序设计中的一种重要的方法，它使许多复杂的问题变得简单，容易解决了。递归特点是：函数或过程调用它自己本身。其中直接调用自己称为直接递归，而将A调用B，B以调用A的递归叫做间接递归。

说到递归，可能我最先想到的就是Hanoi

【题目】Hanoi汉诺塔问题

有N个圆盘，依半径大小（半径都不同），自下而上套在A柱上，每次只允许移动最上面一个盘子到另外的柱子上去（除A柱外，还有B柱和C柱，开始时这两个柱子上无盘子），但绝不允许发生柱子上出现大盘子在上，小盘子在下的情况，现要求设计将A柱子上N个盘子搬移到C柱去的方法。

【算法分析】

    本题是典型的递归程序设计题。

    (1)当N=1 时，只有一个盘子，只需要移动一次:A—>C;

    (2)当N=2时，则需要移动三次：

        A------ 1 ------> B,       A ------ 2 ------> C,       B ------ 1------> C. 

    (3)如果N=3，则具体移动步骤为：

 

 

 

 

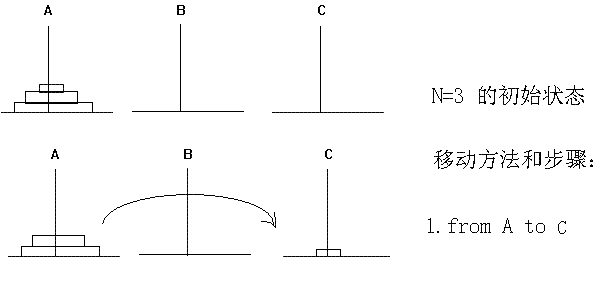
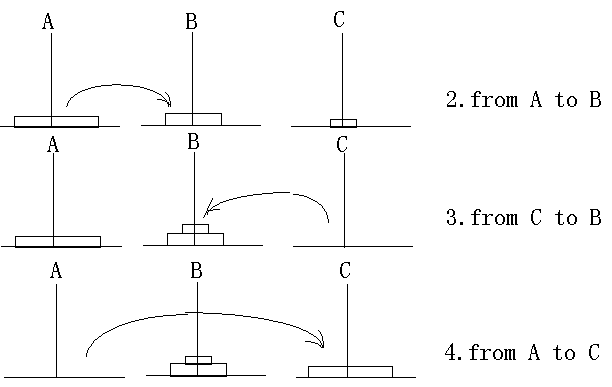
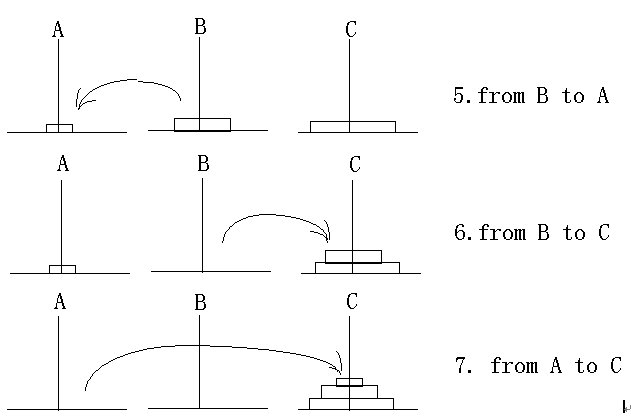
假设把第3步，第4步，第7步抽出来就相当于N=2的情况（把上面2片捆在一起，视为一片）：

 

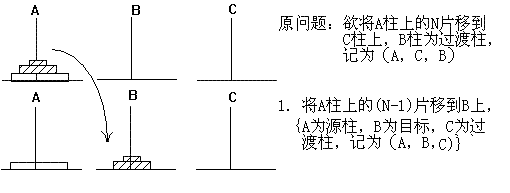
 所以可按“N=2”的移动步骤设计：

①如果N=0，则退出，即结束程序;否则继续往下执行;

②用C柱作为协助过渡，将A柱上的（N-1）片移到B柱上，调用过程mov(n-1, a,b,c);

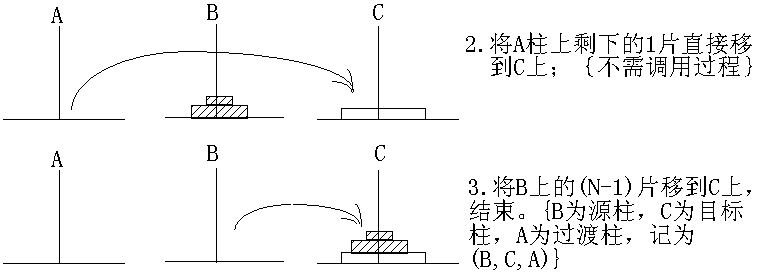
③将A柱上剩下的一片直接移到C柱上;

④用A柱作为协助过渡，将B柱上的（N-1）移到C柱上，调用过程mov (n-1,b,c,a)。

【参考程序】　　　

void mov(int n,char a,char b,char c)

//用b柱作为协助过渡，将a柱上的（n）移到c柱上

{

if(n==0) return;  //如果n=0，则退出，即结束程序

mov(n-1,a,c,b);  //用c柱作为协助过渡，将a柱上的(n-1)片移到b柱上

cout<<++tot<<" "<<a<<" "<<c<<endl;

mov(n-1,b,a,c);  //用a柱作为协助过渡，将b柱上的(n-1)移到c柱上

}　　　

 

程序定义了把n片从A柱移到C柱的过程mov (n,a,c,b)，这个过程把移动分为以下三步来进行：

①先调用过程mov (n-1, a, b, c)，把(n-1)片从A柱移到B柱, C柱作为过渡柱;

②直接执行 writeln(a, ’--＞’, c)，把A柱上剩下的一片直接移到C柱上，;

③调用mov (n-1,b,c,a)，把B柱上的(n-1)片从B移到C柱上，A柱是过渡柱。

对于B柱上的(n-1)片如何移到C柱，仍然调用上述的三步。只是把(n-1)当成了n，每调用一次，要移到目标柱上的片数N就减少了一片，直至减少到n=0时就退出，不再调用。exit是退出指令，执行该指令能在循环或递归调用过程中一下子全部退出来。

我们将1-10的答案输出可以发现，答案与2的N次方有关，进一步发现F[n]=2^n-1,很有点意思哦

  

 

【总结】：

1. 对发现需要递归重要的特点为，在解决一个问题时，发现可以再解决在下一层子问题，再返回相应需要的值
2. 递归的层数一定要注意，怎样解决无限递归，设置递归边界
3. 尽量使递归问题记录下来，以便之后递归到此可以直接返回
4. 递归程序最好循环输出答案，一般来说可以得出递推公式,就是之后特别强的Dp状态转移方程啦

感谢各位与信奥一本通的鼎力相助！