红黑树-想说爱你不容易
前言:
记得在大一懵懵懂懂的时候就接触了红黑树的算法。但由于当时内功尚浅,无法将其内化,只是觉得它很神奇,是个好算法,设计它的人很牛!现今重拾起这个算法,不得不再次被它的精妙所折服!编写本文,是希望以鄙人的理解将红黑树算法的精髓向博客园的园友陈述一番,也希望对其有独特见解的朋友能不吝赐教。准备好了的话,我们就开始吧~
--------------------------------------------
Part I:BST
作为开始,我们得先谈谈二叉树(Binary Search Tree)。
1.假设存在一个如下简单的键值字符表:
Key Value
A 2
C 1
B 6
B 11
H 1
J 3
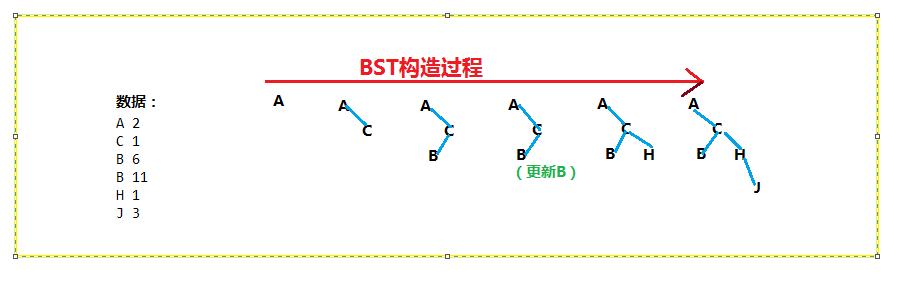
要求你按照读入顺序建立这样一棵二叉查找树,建好之后要求能够进行对于的查询操作。
源于二分查找的思想,二叉查找树有这样一个特点:
对于树上的任意一个结点,如果它有左右子结点的话,其结点大小必定大于其左子结点且小于其右子结点。
2.查找get(key)
由于单独建立一个二叉查找树起初不好分析,我们就假设现在有一棵已经构造好二叉查找树。我们仅需要思考如何在其上面进行查找操作。
根据二分查找的思想,我们可以按照下面步骤进行查找:
Step1:将需要查找的key与二叉查找树的当前根节点的key作比较,得到比较结果后进行下面的step2;
Step2:若查找的key比根节点的key小,则递归从根节点的左子树进行同样的查找key操作;若比根节点的key大,则递归地从根节点的右子树进行同样的查找key操作;
若,查找的key刚好等于当前根节点的key,则返回当前key对应的value,结束!
3.插入put(key,value)
假设现在已经有了一个二叉查找树,我们要插入一对键值(key-value)。源于查找过程的经验,我们知道插入操作其实近似于查找操作。因为,我们插入的时候同样是拿key跟当前根节点的key比较,之后再确定是往左走还是右走,或者是更新当前值(key=root.key时)。
Code:
1 package com.gdufe.binarysearchtree; 2 3 import java.io.File; 4 import java.util.Scanner; 5 6 public class BST<Key extends Comparable<Key>, Value> { 7 8 Node root; // 维护根节点 9 10 class Node { // 二叉树的结点 11 Key key; 12 Value value; 13 Node left, right; 14 15 public Node(Key key, Value value) { // 初始化结点 16 this.key = key; 17 this.value = value; 18 } 19 } 20 21 public Value get(Key key) { 22 return get(root, key); 23 } 24 25 //查找操作 26 public Value get(Node x, Key key) { 27 if (x == null) 28 return null; 29 int cmp = key.compareTo(x.key); 30 if (cmp < 0) 31 return get(x.left, key); 32 else if (cmp > 0) 33 return get(x.right, key); 34 else 35 return x.value; 36 } 37 38 public void put(Key key, Value value) { 39 root = put(root, key, value); 40 } 41 //插入操作 42 public Node put(Node x, Key key, Value value) { 43 if (x == null) 44 return new Node(key, value); 45 int cmp = key.compareTo(x.key); 46 if (cmp < 0) 47 x.left = put(x.left, key, value); 48 else if (cmp > 0) 49 x.right = put(x.right, key, value); 50 else 51 x.value = value; 52 return x; 53 } 54 55 public static void main(String[] args) throws Exception { 56 Scanner input = new Scanner(new File("data_BST.txt")); 57 BST<String, Integer> bst = new BST<String, Integer>(); 58 while (input.hasNext()) { 59 String key = input.next(); 60 int value = input.nextInt(); 61 bst.put(key, value); 62 } 63 System.out.println(bst.get("H")); 64 System.out.println(bst.get("B")); 65 } 66 67 }
输出结果:
1 11
分析:
插入或查找时,有可能最坏情况树不断恶意生长(垂直生长),此时的时间复杂度为:O(N),平均的时间复杂度为:O(lgN)
----------------------------------------
Part II:RedBlackBST
1. 2-3树
在二叉树的基础之上,我们引入了平衡2-3树。简单地说,二叉树每个结点至多只能有2个子结点(称为“2结点”),而现在我们可以通过将2个结点“绑”在一起形成一个有3个子结点的“3结点”。见下图:

由于查找操作较简单,我们重点讨论它的插入操作。同样基于上面所给的数据,见图:

------------------------------------------------
2.红黑二叉查找树(简称“红黑树”)
那么问题来了,我们该如何实现这样一棵2-3树呢?正常的思维当然是希望在原先的Node结构中进行重构,再构造一个嵌套的BIGNode。但巧妙的地方就在这里,我们可以以之前的二叉查找树为基础,把结点之间的链接分为“红链接”和“黑链接”。其中,红连接通过连接两个2结点组成3结点,黑连接是之前二叉查找树的普通连接。为了方便,我们不妨把3结点统一表示为一条左斜的红色链接。如图:
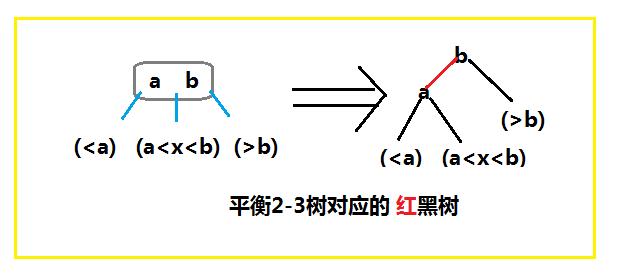
上面通过定义红黑树的规则实现我们等价的2-3树结构,于是红黑树也就有了下面等价的定义。
含有红黑链接并且满足下列条件的二叉查找树:
1)红链接均为左链接
2)没有任何结点同时和2条红链接相连
3)任意空链接到根节点路径上的黑链接数相同
---------------------------------------------
既然从上面的阐述中,我们得出 了“红黑树≈2-3树",我们我们紧接着用上面的数据构建我们的红黑树,见图:
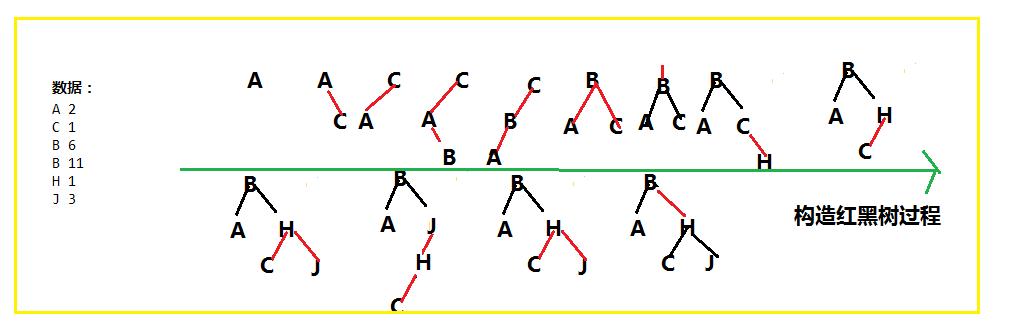
其中,存在着3个关键操作:
左旋:当结点出现左子结点为黑,右子结点为红时,进行左旋转;
右旋:当结点出现左子结点以及左子结点的左结点均为红时,进行右旋转;
变色:当结点出现左右子结点均为红时,进行变色操作(2个子链接均变黑色,并将红链接向上传递!)
具体,见下图: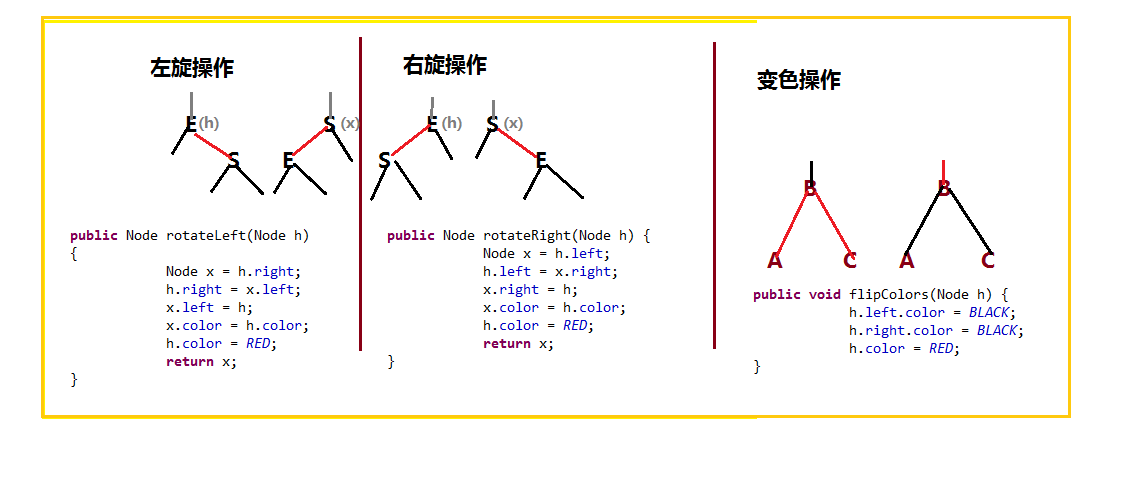
Code:
1 package com.gdufe.binarysearchtree; 2 3 import java.io.File; 4 import java.util.Scanner; 5 6 public class RedBlackTree<Key extends Comparable<Key>, Value> { 7 8 Node root; // 维护根节点 9 10 final static boolean RED = true; 11 final static boolean BLACK = false; 12 13 class Node { // 二叉树的结点 14 Key key; 15 Value value; 16 boolean color; 17 Node left, right; 18 19 public Node(Key key, Value value, boolean color) { // 初始化结点 20 this.key = key; 21 this.value = value; 22 this.color = color; 23 } 24 } 25 26 public Value get(Key key) { 27 return get(root, key); 28 } 29 30 // 右旋 31 public Node rotateRight(Node h) { 32 Node x = h.left; 33 h.left = x.right; 34 x.right = h; 35 x.color = h.color; 36 h.color = RED; 37 return x; 38 } 39 40 // 左旋 41 public Node rotateLeft(Node h) { 42 Node x = h.right; 43 h.right = x.left; 44 x.left = h; 45 x.color = h.color; 46 h.color = RED; 47 return x; 48 } 49 50 // 变色处理 51 public void flipColors(Node h) { 52 h.left.color = BLACK; 53 h.right.color = BLACK; 54 h.color = RED; 55 } 56 public boolean isRed(Node x){ 57 if(x==null) return false; 58 else return x.color; 59 } 60 public Value get(Node x, Key key) { 61 if (x == null) 62 return null; 63 int cmp = key.compareTo(x.key); 64 if (cmp < 0) 65 return get(x.left, key); 66 else if (cmp > 0) 67 return get(x.right, key); 68 else 69 return x.value; 70 } 71 72 public void put(Key key, Value value) { 73 root = put(root, key, value); 74 root.color = BLACK; 75 } 76 77 public Node put(Node x, Key key, Value value) { 78 if (x == null) 79 return new Node(key, value, RED); // 添加的结点链接为红色 80 int cmp = key.compareTo(x.key); 81 if (cmp < 0) 82 x.left = put(x.left, key, value); 83 else if (cmp > 0) 84 x.right = put(x.right, key, value); 85 else { 86 x.value = value; 87 } 88 // 判断是否需要左旋,右旋,变色操作 89 if (x != null) { 90 if (!isRed(x.left) && isRed(x.right)) 91 x = rotateLeft(x); 92 if (isRed(x.left) && isRed(x.left.left)) 93 x = rotateRight(x); 94 if (isRed(x.left ) && isRed(x.right)) 95 flipColors(x); 96 } 97 98 return x; 99 } 100 101 public static void main(String[] args) throws Exception { 102 Scanner input = new Scanner(new File("data_BST.txt")); 103 RedBlackTree<String, Integer> bst = new RedBlackTree<String, Integer>(); 104 while (input.hasNext()) { 105 String key = input.next(); 106 int value = input.nextInt(); 107 bst.put(key, value); 108 } 109 System.out.println(bst.get("H")); 110 System.out.println(bst.get("B")); 111 } 112 113 }
输出结果:
1 11
分析:
有了上面3个关键操作之后,我们保证了树的平衡性,即树不会再恶意生长。插入N个结点后,树的高度为:O(lgN)~O(2*lgN) (思考一下?)。所以,我们得到插入和查找的整体时间复杂度均降为:O(lgN)。
--------------------------
结语:
不得不承认,红黑树算法堪称算法研究领域的非凡之作。在现今的汪洋信息时代,存在着上亿的数据。但是,当我们用红黑树算法对其进行动态的增加和查找时,仅仅需要几十次操作即可完事儿,怎能不让人拍案叫绝!!




