14 深度学习-卷积

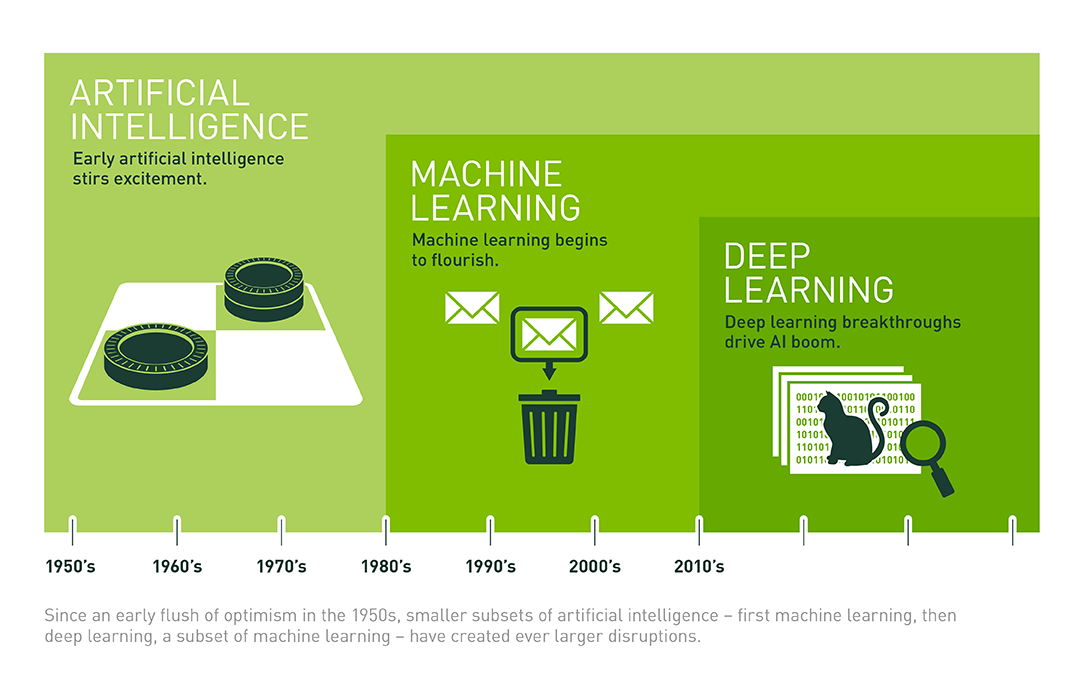
1.简述人工智能、机器学习和深度学习三者的联系与区别。

 

 

2. 全连接神经网络与卷积神经网络的联系与区别。

神经网络即指人工神经网络，或称作连接模型，它是一种模仿动物神经网络行为特征，进行分布式并行信息处理的算法数学模型。这种网络依靠系统的复杂程度，通过调整内部大量节点之间相互连接的关系，从而达到处理信息的目的。神经网络用到的算法是向量乘法，采用符号函数及其各种逼近。并行、容错、可以硬件实现以及自我学习特性，是神经网络的几个基本优点，也是神经网络计算方法与传统方法的区别所在。

3.理解卷积计算。

以digit0为例，进行手工演算。

 

 

from sklearn.datasets import load_digits #小数据集8*8

digits = load_digits()

4.理解卷积如何提取图像特征。

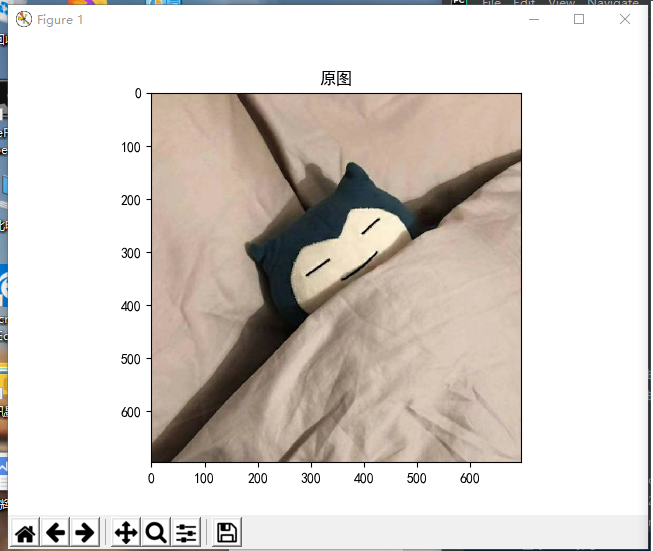
读取一个图像；

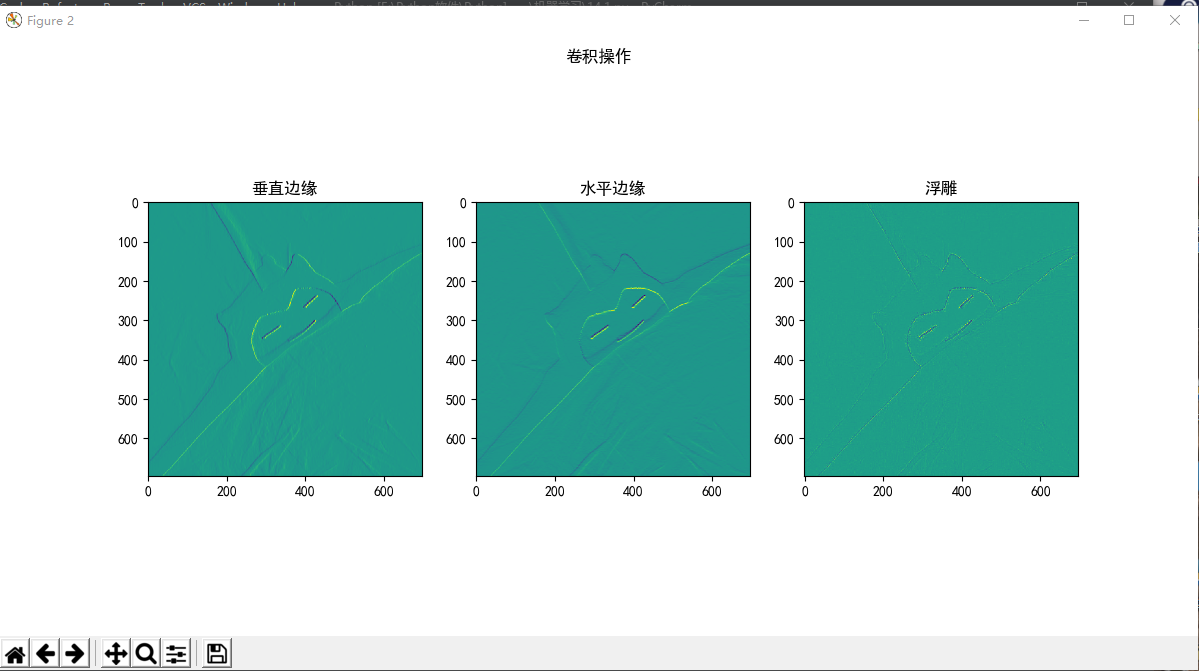
以下矩阵为卷积核进行卷积操作；

显示卷积之后的图像，观察提取到什么特征。

 

1	0	-1
1	0	-1
1	0	-1

 

1	1	1
0	0	0
-1	-1	-1

 

-1	-1	-1
-1	8	-1
-1	-1	-1

 

卷积API

scipy.signal.convolve2d

tf.keras.layers.Conv2D

from PIL import Image
import matplotlib.pyplot as plt
import numpy as np
from scipy.signal import convolve2d

plt.rcParams['font.sans-serif'] = 'SimHei'  # 设置中文显示
I = Image.open(r'D:\yellow.jpg')
L = I.convert('L')

image = np.array(I)
images = np.array(L)
# k = np.array([[-1, 0, 1], [-2, 0, 2], [-1, 0, 1]])
k1 = np.array([[1, 0, -1], [1, 0, -1], [1, 0, -1]])  # 垂直边缘
k2 = np.array([[1, 1, 1], [0, 0, 0], [-1, -1, -1]])  # 水平边缘
k3 = np.array([[-1, -1, -1], [-1, 8, -1], [-1, -1, -1]])  # 浮雕

# image = convolve2d(images, k, boundary='symm', mode='same')
image1 = convolve2d(images, k1, boundary='symm', mode='same')  # 垂直边缘
image2 = convolve2d(images, k2, boundary='symm', mode='same')  # 水平边缘
image3 = convolve2d(images, k3, boundary='symm', mode='same')  # 浮雕

plt.imshow(image)  # 原图
plt.title("原图")
plt.figure(figsize=(12, 6))  # 定制大小画布
plt.suptitle("卷积操作")
plt.subplot(1, 3, 1)  # 放置的一行三列，位置1
plt.imshow(image1)  # 垂直边缘
plt.title("垂直边缘")
plt.subplot(1, 3, 2)  # 放置的一行三列，位置2
plt.imshow(image2)  # 水平边缘
plt.title("水平边缘")
plt.subplot(1, 3, 3)  # 放置的一行三列，位置3
plt.imshow(image3)  # 浮雕
plt.title("浮雕")

 

 

 

 

5. 安装Tensorflow,keras