排序算法(二)
目录
上一篇文章中我们总结了常用的比较排序算法,主要有冒泡排序,选择排序,插入排序,归并排序,堆排序,快速排序等。
这篇文章中我们来探讨一下常用的非比较排序算法:计数排序,基数排序,桶排序。在一定条件下,它们的时间复杂度可以达到O(n)。
这里我们用到的唯一数据结构就是数组,当然我们也可以利用链表来实现下述算法。
计数排序(Counting Sort)
计数排序用到一个额外的计数数组C,根据数组C来将原数组A中的元素排到正确的位置。
通俗地理解,例如有10个年龄不同的人,假如统计出有8个人的年龄不比小明大(即小于等于小明的年龄,这里也包括了小明),那么小明的年龄就排在第8位,通过这种思想可以确定每个人的位置,也就排好了序。当然,年龄一样时需要特殊处理(保证稳定性):通过反向填充目标数组,填充完毕后将对应的数字统计递减,可以确保计数排序的稳定性。
计数排序的步骤如下:
- 统计数组A中每个值A[i]出现的次数,存入C[A[i]]
- 从前向后,使数组C中的每个值等于其与前一项相加,这样数组C[A[i]]就变成了代表数组A中小于等于A[i]的元素个数
- 反向填充目标数组B:将数组元素A[i]放在数组B的第C[A[i]]个位置(下标为C[A[i]] - 1),每放一个元素就将C[A[i]]递减
计数排序的实现代码如下:
#include<iostream>
using namespace std;
// 分类 ------------ 内部非比较排序
// 数据结构 --------- 数组
// 最差时间复杂度 ---- O(n + k)
// 最优时间复杂度 ---- O(n + k)
// 平均时间复杂度 ---- O(n + k)
// 所需辅助空间 ------ O(n + k)
// 稳定性 ----------- 稳定
const int k = 100; // 基数为100,排序[0,99]内的整数
int C[k]; // 计数数组
void CountingSort(int A[], int n)
{
for (int i = 0; i < k; i++) // 初始化,将数组C中的元素置0(此步骤可省略,整型数组元素默认值为0)
{
C[i] = 0;
}
for (int i = 0; i < n; i++) // 使C[i]保存着等于i的元素个数
{
C[A[i]]++;
}
for (int i = 1; i < k; i++) // 使C[i]保存着小于等于i的元素个数,排序后元素i就放在第C[i]个输出位置上
{
C[i] = C[i] + C[i - 1];
}
int *B = (int *)malloc((n) * sizeof(int));// 分配临时空间,长度为n,用来暂存中间数据
for (int i = n - 1; i >= 0; i--) // 从后向前扫描保证计数排序的稳定性(重复元素相对次序不变)
{
B[--C[A[i]]] = A[i]; // 把每个元素A[i]放到它在输出数组B中的正确位置上
// 当再遇到重复元素时会被放在当前元素的前一个位置上保证计数排序的稳定性
}
for (int i = 0; i < n; i++) // 把临时空间B中的数据拷贝回A
{
A[i] = B[i];
}
free(B); // 释放临时空间
}
int main()
{
int A[] = { 15, 22, 19, 46, 27, 73, 1, 19, 8 }; // 针对计数排序设计的输入,每一个元素都在[0,100]上且有重复元素
int n = sizeof(A) / sizeof(int);
CountingSort(A, n);
printf("计数排序结果:");
for (int i = 0; i < n; i++)
{
printf("%d ", A[i]);
}
printf("\n");
return 0;
}
下图给出了对{ 4, 1, 3, 4, 3 }进行计数排序的简单演示过程
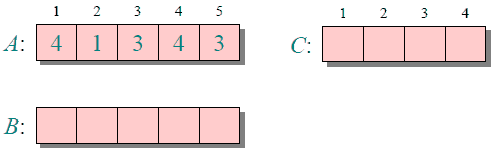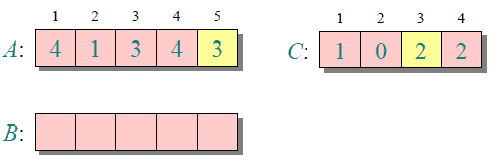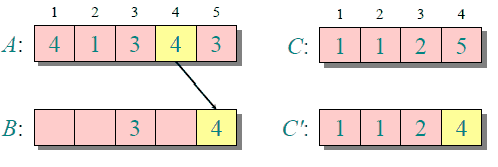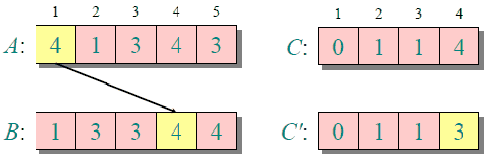
计数排序的时间复杂度和空间复杂度与数组A的数据范围(A中元素的最大值与最小值的差加上1)有关,因此对于数据范围很大的数组,计数排序需要大量时间和内存。
例如:对0到99之间的数字进行排序,计数排序是最好的算法,然而计数排序并不适合按字母顺序排序人名,将计数排序用在基数排序算法中,能够更有效的排序数据范围很大的数组。
基数排序(Radix Sort)
基数排序的发明可以追溯到1887年赫尔曼·何乐礼在打孔卡片制表机上的贡献。它是这样实现的:将所有待比较正整数统一为同样的数位长度,数位较短的数前面补零。然后,从最低位开始进行基数为10的计数排序,一直到最高位计数排序完后,数列就变成一个有序序列(利用了计数排序的稳定性)。
基数排序的实现代码如下:
#include<iostream>
using namespace std;
// 分类 ------------- 内部非比较排序
// 数据结构 ---------- 数组
// 最差时间复杂度 ---- O(n * dn)
// 最优时间复杂度 ---- O(n * dn)
// 平均时间复杂度 ---- O(n * dn)
// 所需辅助空间 ------ O(n * dn)
// 稳定性 ----------- 稳定
const int dn = 3; // 待排序的元素为三位数及以下
const int k = 10; // 基数为10,每一位的数字都是[0,9]内的整数
int C[k];
int GetDigit(int x, int d) // 获得元素x的第d位数字
{
int radix[] = { 1, 1, 10, 100 };// 最大为三位数,所以这里只要到百位就满足了
return (x / radix[d]) % 10;
}
void CountingSort(int A[], int n, int d)// 依据元素的第d位数字,对A数组进行计数排序
{
for (int i = 0; i < k; i++)
{
C[i] = 0;
}
for (int i = 0; i < n; i++)
{
C[GetDigit(A[i], d)]++;
}
for (int i = 1; i < k; i++)
{
C[i] = C[i] + C[i - 1];
}
int *B = (int*)malloc(n * sizeof(int));
for (int i = n - 1; i >= 0; i--)
{
int dight = GetDigit(A[i], d); // 元素A[i]当前位数字为dight
B[--C[dight]] = A[i]; // 根据当前位数字,把每个元素A[i]放到它在输出数组B中的正确位置上
// 当再遇到当前位数字同为dight的元素时,会将其放在当前元素的前一个位置上保证计数排序的稳定性
}
for (int i = 0; i < n; i++)
{
A[i] = B[i];
}
free(B);
}
void LsdRadixSort(int A[], int n) // 最低位优先基数排序
{
for (int d = 1; d <= dn; d++) // 从低位到高位
CountingSort(A, n, d); // 依据第d位数字对A进行计数排序
}
int main()
{
int A[] = { 20, 90, 64, 289, 998, 365, 852, 123, 789, 456 };// 针对基数排序设计的输入
int n = sizeof(A) / sizeof(int);
LsdRadixSort(A, n);
printf("基数排序结果:");
for (int i = 0; i < n; i++)
{
printf("%d ", A[i]);
}
printf("\n");
return 0;
}
下图给出了对{ 329, 457, 657, 839, 436, 720, 355 }进行基数排序的简单演示过程
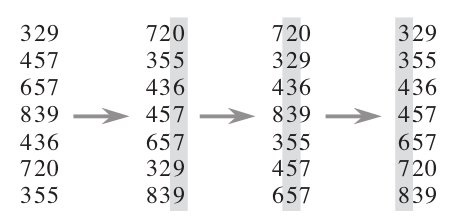
基数排序的时间复杂度是O(n * dn),其中n是待排序元素个数,dn是数字位数。这个时间复杂度不一定优于O(n log n),dn的大小取决于数字位的选择(比如比特位数),和待排序数据所属数据类型的全集的大小;dn决定了进行多少轮处理,而n是每轮处理的操作数目。
如果考虑和比较排序进行对照,基数排序的形式复杂度虽然不一定更小,但由于不进行比较,因此其基本操作的代价较小,而且如果适当的选择基数,dn一般不大于log n,所以基数排序一般要快过基于比较的排序,比如快速排序。由于整数也可以表达字符串(比如名字或日期)和特定格式的浮点数,所以基数排序并不是只能用于整数排序。
桶排序(Bucket Sort)
桶排序也叫箱排序。工作的原理是将数组元素映射到有限数量个桶里,利用计数排序可以定位桶的边界,每个桶再各自进行桶内排序(使用其它排序算法或以递归方式继续使用桶排序)。
桶排序的实现代码如下:
#include<iostream>
using namespace std;
// 分类 ------------- 内部非比较排序
// 数据结构 --------- 数组
// 最差时间复杂度 ---- O(nlogn)或O(n^2),只有一个桶,取决于桶内排序方式
// 最优时间复杂度 ---- O(n),每个元素占一个桶
// 平均时间复杂度 ---- O(n),保证各个桶内元素个数均匀即可
// 所需辅助空间 ------ O(n + bn)
// 稳定性 ----------- 稳定
/* 本程序用数组模拟桶 */
const int bn = 5; // 这里排序[0,49]的元素,使用5个桶就够了,也可以根据输入动态确定桶的数量
int C[bn]; // 计数数组,存放桶的边界信息
void InsertionSort(int A[], int left, int right)
{
for (int i = left + 1; i <= right; i++) // 从第二张牌开始抓,直到最后一张牌
{
int get = A[i];
int j = i - 1;
while (j >= left && A[j] > get)
{
A[j + 1] = A[j];
j--;
}
A[j + 1] = get;
}
}
int MapToBucket(int x)
{
return x / 10; // 映射函数f(x),作用相当于快排中的Partition,把大量数据分割成基本有序的数据块
}
void CountingSort(int A[], int n)
{
for (int i = 0; i < bn; i++)
{
C[i] = 0;
}
for (int i = 0; i < n; i++) // 使C[i]保存着i号桶中元素的个数
{
C[MapToBucket(A[i])]++;
}
for (int i = 1; i < bn; i++) // 定位桶边界:初始时,C[i]-1为i号桶最后一个元素的位置
{
C[i] = C[i] + C[i - 1];
}
int *B = (int *)malloc((n) * sizeof(int));
for (int i = n - 1; i >= 0; i--)// 从后向前扫描保证计数排序的稳定性(重复元素相对次序不变)
{
int b = MapToBucket(A[i]); // 元素A[i]位于b号桶
B[--C[b]] = A[i]; // 把每个元素A[i]放到它在输出数组B中的正确位置上
// 桶的边界被更新:C[b]为b号桶第一个元素的位置
}
for (int i = 0; i < n; i++)
{
A[i] = B[i];
}
free(B);
}
void BucketSort(int A[], int n)
{
CountingSort(A, n); // 利用计数排序确定各个桶的边界(分桶)
for (int i = 0; i < bn; i++) // 对每一个桶中的元素应用插入排序
{
int left = C[i]; // C[i]为i号桶第一个元素的位置
int right = (i == bn - 1 ? n - 1 : C[i + 1] - 1);// C[i+1]-1为i号桶最后一个元素的位置
if (left < right) // 对元素个数大于1的桶进行桶内插入排序
InsertionSort(A, left, right);
}
}
int main()
{
int A[] = { 29, 25, 3, 49, 9, 37, 21, 43 };// 针对桶排序设计的输入
int n = sizeof(A) / sizeof(int);
BucketSort(A, n);
printf("桶排序结果:");
for (int i = 0; i < n; i++)
{
printf("%d ", A[i]);
}
printf("\n");
return 0;
}
下图给出了对{ 29, 25, 3, 49, 9, 37, 21, 43 }进行桶排序的简单演示过程
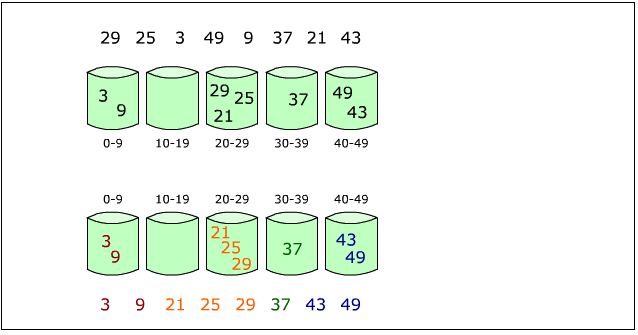
桶排序不是比较排序,不受到O(nlogn)下限的影响,它是鸽巢排序的一种归纳结果,当所要排序的数组值分散均匀的时候,桶排序拥有线性的时间复杂度。




 浙公网安备 33010602011771号
浙公网安备 33010602011771号