2022-08-02 18:19阅读: 80评论: 1推荐: 0

Introduction to Group

Definitions of Group

Group

Definition (Group)

若一个集合 $G$ 和其上的运算 $\circ$ 满足以下四个条件，则称二元组 $(G, \circ)$ 构成群，或称 $G$ 在 $\circ$ 下构成群。在不混淆的情况下，也可称 $G$ 是群。

1. 封闭性： $\forall f, g \in G$ ， $f \circ g \in G$ 。

2. 结合律： $\forall f, g, h \in G$ ， $(f \circ g) \circ h = f \circ (g \circ h)$ 。

3. 单位元存在性： $\exists e \in G$ ，使得 $\forall g \in G$ ， $g \circ e = e \circ g = g$ 。

4. 逆存在性： $\forall f \in G, \exists g \in G$ ，使得 $f \circ g = g \circ f = e$ 。

其中 $e$ 叫 单位元(幺元)，对满足 $f \circ g = g \circ f = e$ 的 $g$ ，称为 $f$ 的逆元，记作 $f^{- 1}$ 。 $f^{- 1}$ 唯一。

Abelian Group (阿贝尔群)

Definition (Abelian Group)

当群 $G$ 的运算满足 交换律 时，我们称 $G$ 是一个 交换群 或 阿贝尔 (Abel) 群。

Special Groups

整数加法群

整数集合 $Z$ 关于加法 $+$ 构成群 $(Z, +)$ 。

Cyclic Group (循环群)

对于任何正整数 $m$ ，在模 $m$ 的意义下的加法也构成群。

这个群非常重要，我们把它称为 $m$ 阶 循环群 (Cyclic Group)，记作 $Z_{m}$ 。

Symmetry Group (对称群)

所有 $n!$ 个 $n$ 元置换构成一个群，这个群被称为 $n$ 元 对称群 (Symmetry Group)，记作 $S_{n}$ 。

Alternating Group (交错群)

可以验证，所有 $⌊ \frac{n!}{2} ⌋$ 个偶置换也构成一个群，这个群被称为 $n$ 元 交错群 (Alternating group) ，记作 $A_{n}$ 。

Dihedral Group (二面体群)

对于一个正 $n$ 边形，它的 旋转群 和 $Z_{n}$ 是“本质相同”的(被称为“同构”)，因此没必要去一个新的名称；

它的 旋转/翻转群 (意思就是把旋转和翻转构成的图形合起来的群) 共有 $2 n$ 个元素，

被称为 $2 n$ 阶 二面体群 (Dihedral Group)，记作 $D_{2 n}$ 。

Order (阶)

Definition (Order)

群 $G$ 的元素个数称为 $G$ 的阶，简记为 $| G |$ 。

若群 $G$ 有无穷多个元素，称 $G$ 为 无限群；

否则称 $G$ 为 有限群。

元和阶的概念不一样，不能乱用。

对于置换来说，元就是每个置换的元素个数，而不是置换群的元素(置换)个数。

$(Z, +)$ 为无限群。
$| Z_{m} | = m$ 。
$| S_{n} | = n!$ 。
$| A_{n} | = ⌊ \frac{n!}{2} ⌋$ 。
$| D_{2 n} | = 2 n$ 。

Subgroup (子群)

Subgroup

Definition (Subgroup)

设 $(G, \circ)$ 是群，若 $(G, \circ)$ 的子集 $(H, \circ)$ 对 同一种运算 $\circ$ 也构成群，

则称 $(H, \circ)$ 是 $(G, \circ)$ 的子群，记作 $(H, \circ) \leq (G, \circ)$ 。

$A_{n} \leq S_{n}$ 。
$Z_{n} \leq Z_{m} ⟺ n | m$ 。
$Z_{m} ≰ (Z, +)$ ，因为前者是模意义下的加法，后者是普通加法，两者不是同一种运算。

Generated Subgroup (生成子群)

Definition (Generated Subgroup)

设 $(G, \circ)$ 是群， $S$ 为 $G$ 的一个 非空子集，

则把包含 $S$ 的所有子群的交称为 $S$ 在 $G$ 中生成的子群，记作 $< S >$ 。

Lagrange Theory (拉格朗日定理)

Coset (陪集)

Coset

Definition (Ceset)

对于群 $G$ 和它的子群 $H \leq G$ ，对于一个元素 $g \in G$ ，记集合 $g H = {g \circ h | h \in H}$ 为 $H$ 在 $G$ 中导出的一个左陪集，同理可以定义右陪集。

在多数情况下，陪集不是子群。

Properties of Coset

我们只讨论右陪集，左陪集同理。

Property 1

Property 1

$\forall g \in G$ ， $| H | = | H g |$ 。

由于逆元唯一，对于 $h_{1}, h_{2} \in H, h_{1} \neq h_{2}$ ，有 $h_{1} \circ g \neq h_{2} \circ g$ 。

所以每一个 $h$ 对应一个 $h g$ ，这些 $h g$ 互不相同，因此 $| H | = | H g |$ 。

Property 2

Property 2

$\forall g \in G$ ， $g \in H g$ 。

由于 $H$ 是个群，且与 $G$ 是同一个运算，因此也包含幺元 $e$ ， $e \circ g = g$ ，因此 $g \in H g$ 。

Property 3

Property 3

$H g = H ⟺ g \in H$ 。

$p \to q$ ： $H g$ 也是个群， $g$ 与 $H$ 内的元素进行运算得到群内元素，由群的封闭性， $g$ 必须包含在群内。

$q \to p$ ：仍然看作是 $H$ 群内元素的运算，由封闭性可知。

Property 4

Property 4

$H a = H b ⟺ a \circ b^{- 1} \in G$ 。

$p \to q$ ：由 $H a = H b$ ，有 $H a \circ b^{- 1} = H$ 。又由性质 3， $a \circ b^{- 1} \in G$ 。(其实这种写法不太严谨...)

$q \to p$ ：同由性质 3。反过来推就行了。

Property 5

Property 5

$H a \cap H b \neq \emptyset ⟺ H a = H b$ 。

这条性质很有用。

即对于 $H$ 的任意两个左/右陪集，它们要么相等要么完全不相交。

设 $c \in H a$ 且 $c \in H b$ ，则 $\exists h_{1}, h_{2} \in H$ ，使得 $h_{1} \circ a = h_{2} \circ b = c$ ，

移项得 $a \circ b^{- 1} = h_{2} \circ h_{1}^{- 1} \in H$ 。由性质 4， $H a = H b$ 。

那么其实可以打双箭头了。

Property 6

Property 6

$H$ 的全体左/右陪集的并为 $G$ 。

由于 $e \in H$ ， $g$ 取遍 $G$ 中的所有元素，显然。逃

Lagrange Theory

Lagrange Theory

$| H | \times [G : H] = | G |$

这里引入一个表述：

Definition

若 $H \leq G$ ，则 $[G : H]$ 表示 $G$ 中 $H$ 的不同陪集的数量。

$H$ 的陪集大小均为 $| H |$ ，它们要么不相交要么相等，全体陪集并为 $G$ ，于是拉格朗日定理显然成立。

接下来在一般群的定义上，引入关于置换群的特殊概念。

Coloring (染色)

Coloring

Definition (Coloring)

一个 $n$ 元染色，指的是对集合 $[n]$ 的每个元素分配一个物品(可以是颜色、数，等等) 的分配方案。

比如，当 $n = 3$ 时， ${1 \to 红, 2 \to 绿, 3 \to 粉}$ 是一个染色， ${1 \to 123, 2 \to 254, 3 \to 357}$ 也是一个染色。

Action (作用)

置换群相对于其它的群有一个好处，它的元素是置换。而置换，是可以作用于染色的。

Definition (Action)

对于置换 $f \in S_{n}$ 和染色 $c \in C$ ，定义满足 $f (i)$ 的颜色是 $c [i]$ 的染色 $c^{^{'}}$ ，为 $f$ 作用于 $c$ 的结果，记为 $f \cdot c$ ，简记为 $f c$ 。即 $(f \cdot c) [i] = c [f^{- 1} (i)]$ 。

可见，置换作用于染色后的结果仍是染色。

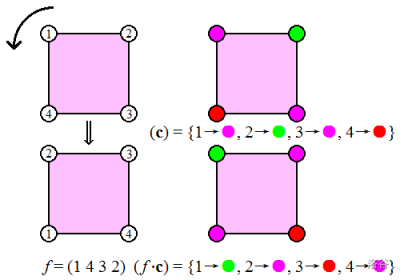
置换对染色满足以下两个 十分重要 性质：

$e \cdot c = c$ 。
$(f \circ g) \cdot c = f \cdot (g \cdot c)$ 。

通过这两个性质可以得到抽象的染色概念：

Generalized Coloring

Definition (Generalized Coloring)

对于群 $G$ (无须是置换群) 和一个全集 $C$ ，对于 $G$ 中任意一个元素和 $C$ 中任意一个元素 $c$ ，

定义运算 $\cdot$ 满足 $g \cdot c \in C$ ，且满足如下两个性质：

$e \cdot c = c$ 。

$(f \circ g) \cdot c = f \cdot (g \cdot c)$ 。

则称 $C$ 是广义染色集合， $C$ 中的元素 $c$ 是广义染色。

$C$ 是一个无穷集合。

Orbit-stabilizer Theorem (轨道-稳定子群定理)

Orbit (轨道)

Definition (Orbit)

考虑一个群 $G$ 和一个染色 $c$ ，将群中所有元素都对 $c$ 作用，得到一个 $C$ 的子集，记作 $G \cdot c$ 。

$G \cdot c = {g \cdot c | g \in G}$
这个染色集合 $G \cdot c$ 被称为 $c$ 在 $G$ 中的轨道。

$| G \cdot c | \leq | G |$ 。在染色集合 $G \cdot c$ 中，一个染色可对应多个群中元素。

Definition (fixed)

对一个染色集合 $X \subseteq C$ ，定义 $G \cdot X = {g \cdot c | g \in G, c \in X}$ 。

若 $G \cdot X = X$ ，则称 $X$ 在 $G$ 下 固定 (fixed)。

可以理解为，给了 $G$ 一个固定的运算，即使 $X$ 要染成哪些颜色无法确定，每个 $X$ 也都都是有限的。

不同的颜色可以导出不同的染色集合 $X$ ，因此颜色导致 $X$ 的个数无限。

Stabilizer Subgroup (稳定子群)

Definition (Stabilizer Subgroup)

对于一个置换群 $G$ 和一个染色 $c$ ，群中满足 $g \cdot c = c$ 的置换 $g$ 构成一个群，

称为染色 $c$ 的 稳定子群，记作 $G_{c}$ 。

$G_{c}$ 中的元素可称作 稳定子。

$G_{c}$ 构成群，这一点可以由定义证明：

单位元存在性显然， $e \cdot c = c$ 。
逆元存在性：

考虑 $g \cdot c = c ⟺ g^{- 1} \cdot (g \cdot c) = g^{- 1} \cdot c ⟺ (g^{- 1} \circ g) \cdot c = g^{- 1} \cdot c ⟺ g^{- 1} \cdot c = c$ 。

即若 $g$ 在 $G_{c}$ 内， $g^{- 1}$ 也在 $G_{c}$ 内。
结合律：置换的合成显然满足。
封闭性：设有 $f \cdot c = c, g \cdot c = c$ ，考虑代换： $f \cdot (g \cdot c) = c ⟺ (f \circ g) \cdot c = c$ 。

即 $f \circ g$ 也在 $G_{c}$ 内，满足封闭性。

Orbit-stabilizer Theorem

Orbit-stabilizer Theorem

对于置换群 $G$ 和染色 $c$ ，有：

$| G \cdot c | \times | G_{c} | = | G |$

Proof：

上文已证 $G_{c}$ 是 $G$ 的子群。

任取 $G$ 中的元素 $g$ ，对左陪集 $g G_{c} = {g \circ h | h \in G_{c}}$ 中的元素 $f = g \circ h_{0}$ ，

有 $f \cdot c = (g \circ h_{0}) \cdot c = g \cdot (h_{0} \cdot c) = g \cdot c$ ，

因此 左陪集 $g G_{c}$ 中的所有置换作用于 $c$ 产生相同的一种染色 $g \cdot c$ 。

另一方面，对于两个不同的左陪集 $g_{1} G_{c}, g_{2} G_{c}$ ，它们作用于 $c$ 不能产生相同的染色。

补证：若它们能产生相同的染色，由上面的论述，只需把 $g_{1} \cdot c$ 与 $g_{2} \cdot c$ 拿出来考察，

由我们的假设， $g_{1} \cdot c = g_{2} \cdot c ⟺ g_{2}^{- 1} \cdot (g_{1} \cdot c) = c ⟺ (g_{2}^{- 1} \circ g_{1}) \cdot c = c$ 。

由稳定子群的定义， $g_{2}^{- 1} \circ g_{1} \in G_{c}$ 。

由陪集性质 4， $g_{2}^{- 1} \circ g_{1} \in G_{c} ⟺ g_{1} G_{c} = g_{2} G_{c}$ ，与假设矛盾，因此原命题成立。

总结一下前面两步，对于稳定子群 $G_{c}$ ，先证明了同一陪集引出同一染色，以此为基础证明了不同陪集引出不同染色。

$G_{c}$ 导出的不同陪集的数量为 $[G : G_{c}]$ ，而这也正是能导出的不同染色的数量。

$G_{c}$ 作为 $G$ 的一个子群，它的所有陪集的并为 $G$ ，因此这些陪集能导出的染色集合就是 $G \cdot c$ ，即 $[G : G_{c}] = | G \cdot c |$ 。

由拉格朗日定理， $| G | = | G_{c} | \times | G : G_{c} | = | G_{c} | \times | G \cdot c |$ 。

轨道大小 $\times$ 稳定子群大小 = 原群大小

上一篇Permutation (排列与置换)

下一篇AGC002F Leftmost Ball

本文作者：Schucking_Sattin

本文链接：https://www.cnblogs.com/Schucking-Sattin/p/16544782.html

posted @ 2022-08-02 18:19 Schucking_Sattin 阅读(80) 评论(1) 编辑收藏举报

刷新页面返回顶部

登录后才能查看或发表评论，立即登录或者逛逛博客园首页