【算法学习】匈牙利算法
匈牙利算法
一、历史
匈牙利算法是一种在多项式时间内求解任务分配问题的组合优化算法，广泛应用在运筹学领域， 美国数学家哈罗德·库恩于1955年提出该算法，之所以被称作匈牙利算法是因为算法很大一部分是基于以前匈牙利数学家Dénes Kőnig(1884-1944)和Jenő Egerváry(1891-1958)的工作上创建起来的。
Kuhn H W. The Hungarian method for the assignment problem[J]. Naval research logistics quarterly, 1955, 2(1‐2): 83-97.
原文链接：https://blog.csdn.net/lx_ros/article/details/123980953
二、相关概念
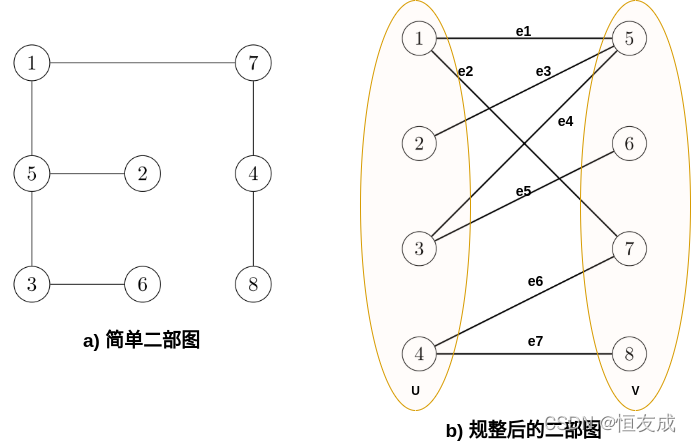
1. 二部图 Bigraph, Bipartite graph
-
二部图（Bipartite graph）是一类特殊的图，也称二分图，
它可以被划分为两个部分，每个部分内的点互不相连。上图是典型的二分图； -
二分图是图论中的一种特殊模型。若能将无向图G=(V,E)的顶点V划分为两个交集为空的顶点集，并且任意边的两个端点都分属于两个集合，则称图G为一个为二分图。
2. 匹配 Matching
- 匹配边、非匹配边和非匹配点；
- 匹配的两个重点：(1) 匹配是边的集合；在该集合中，(2) 任意两条边不能有共同的顶点。
3. 最大匹配 Maximum Matching
- 选择这样的边数最大的子集称为图的最大匹配问题；
- 最大匹配的边数称为最大匹配数。
4. 完全匹配
- 如果一个匹配中，图中的每个顶点都和图中某条边相关联，则称此匹配为完全匹配，也称作完备匹配；
5. 最优匹配
- 又称为带权最大匹配，是指在带有权值边的二分图中，求一个匹配使得匹配边上的权值和最大；
- 一般X和Y集合顶点个数相同，最优匹配也是一个完备匹配，即每个顶点都被匹配。如果个数不相等，可以通过补点加0边实现转化。一般使用KM算法解决该问题。
6. 交错路径
- M是二部图G的一个匹配，G的一条M交错路径是指，其边在M和E(G)-M中交替出现的路径，即从未匹配点出发，依次经过未匹配的边和已匹配的边，即为交替路，如{e2, e7}，则{e1, e2, e6, e7}就是一条交错路径
7. 增广路径
-
在二分图的匹配中，如果一条路径的首尾是非匹配点，路径中除此之外（如果有）其他的点均是匹配点，那么这条路径就是一条增广路径（Agumenting path），从定义可知增广路径是一种特殊的交错路径。结合上面的图可知{e1, e6}是匹配时，{e7, e6, e2 ,e1 ,e3}是一条增广路径。
-
基于上述术语引出Hall定理，图G中的一个匹配M是最大匹配的充分必要条件是G中不存在M的增广路径。证明可参考
-
增广路径的首尾是非匹配点。因此，增广路径的第一条和最后一条边，必然是非匹配边；由交错路径的定义可知，增广路径从非匹配边开始，匹配边和非匹配边依次交替，最后由非匹配边结束。这样一来，增广路径中非匹配边的数目总比匹配边大 1。
-
考虑置换增广路径中的匹配边和非匹配边，由于增广路径的首尾是非匹配点，其余则是匹配点，这样的置换不会影响原匹配中其他的匹配边和匹配点，因而不会破坏匹配；而增广路径的置换，可使匹配的边数加1，得到比原有匹配更大的匹配。
-
由于二分图的最大匹配必然存在（比如，上限是包含所有顶点的完全匹配），所以，在任意匹配的基础上，如果有办法不断地搜寻出增广路径，直到最终我们找不到新的增广路径为止，就有可能得到二分图的一个最大匹配。匈牙利算法正是基于这种思想来实现的。
-
二部图的最大匹配可分成有权二部图和无权二部图，无权二部图的实例表示如宠物匹配，有权二部图实例如任务指派。无权二部图的最大匹配不能使用贪心算法，可以使用网络流问题来进行求解。
-
有权二部图满足约束条件后可使用匈牙利算法来求最大匹配，两边的结点相同∣U∣ = ∣V∣ = n ，匈牙利算法的时间复杂度为 O(n^3).
