- 卷积神经网络中每个网络层输出的特征图中的单个元素映射回原始输入特征中的区域大小，网络层越深，其输出特征的元素对应感受野越大。也就是说输出特征图中单个元素能够看到输入图中多大区域或则说特征图上上某个元素的计算受输入图像上某个区域的影响，这个区域即该元素的感受野。
- 对于全连接网络而言，其输出中的每一个元素都受到输入特征中所有元素的影响，也就是说全连接神经网络的感受野是输入的神经元个数
卷积神经网络的感受野
当前层感受野大小受到当前层卷积核大小、步长以及上一层(左是右的上一层)的感受野共同影响。
计算公式为：
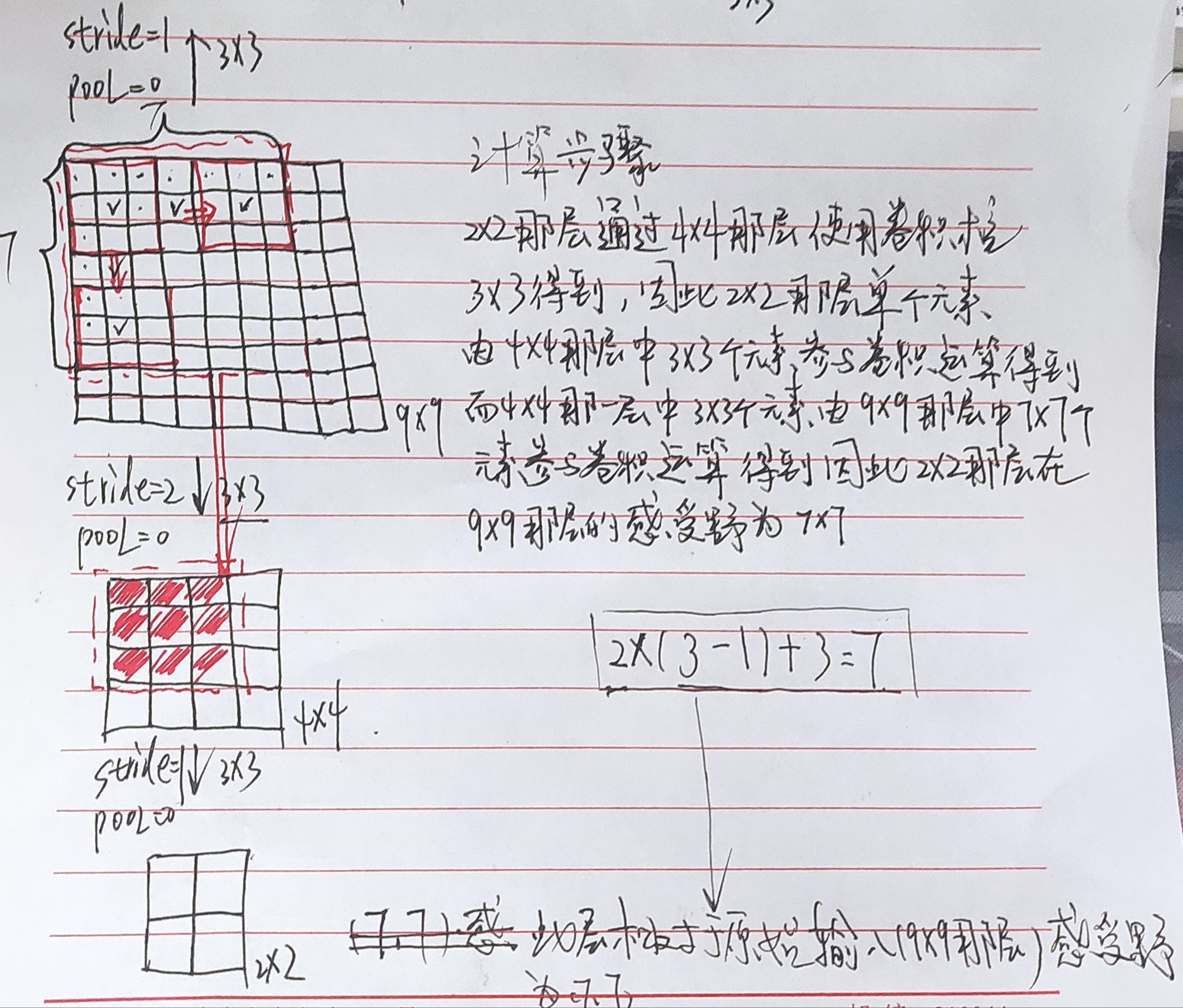
RF、S、K分别表示感受野、步长、卷积核大小，计算第i层输出结果的感受野时，利用上面公式从RF(i)一直计算到RF(1）时，RF(1）即为第i层对应的感受野大小。
Convk+1在Convk的(3,3)输出中感受野大小等于Convk卷积核的大小
例子1：
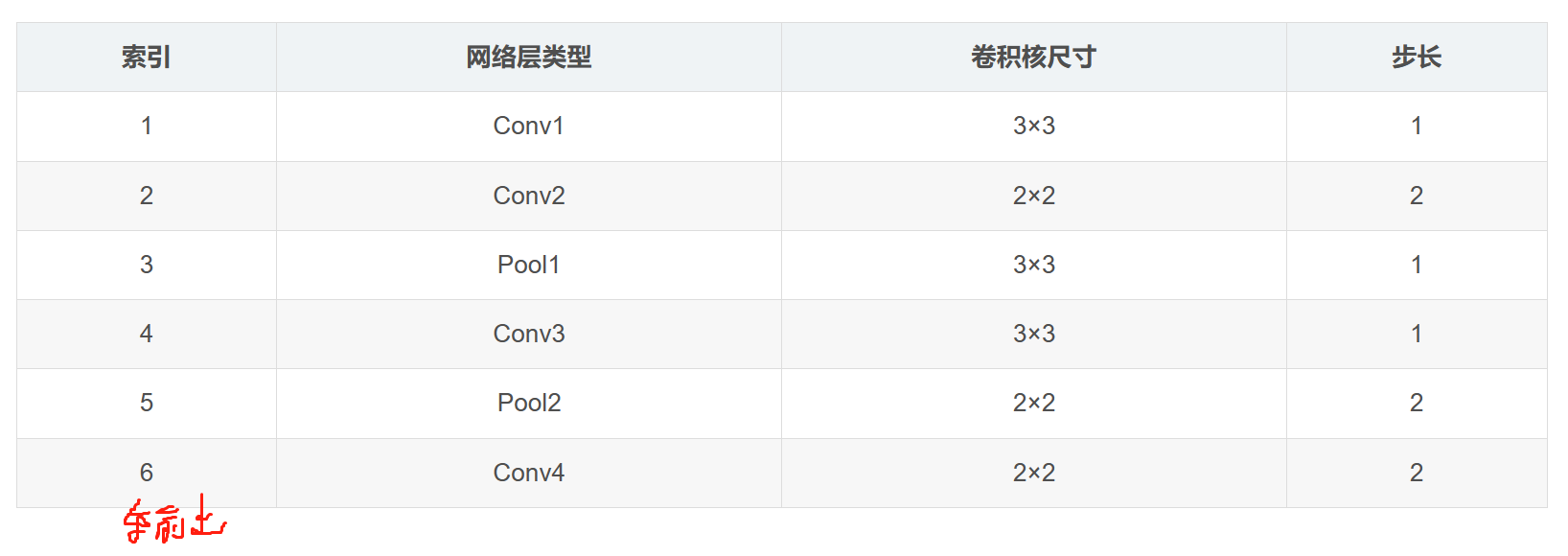
例子2：
使用连续的小卷积核替换单个大卷积核的优点
1.第一可以有效降低网络训练的参数量
比如输入一个C通道的图像，每次都得到C个特征图，每次都使用3*3的卷积核，进行3层卷积，每次的步长为1，最终得到感受野为(7*7)的输出，整体使用的参数数量为3*3*C*C+3*3*C*C+3*3*C*C=27*C*C
其中3*3*C是由于输入有C个通道，因此得到一个特征图必须使用C个3*3的卷积核
3*3*C*C，再乘一个C的原因是此次输出想得到C个特征图
如果一个C通道的图像输入使用7*7的卷积核进行1层卷积，得到一个感受野为(7*7)的C个特征图的输出，所需要的参数为7*7*C*C=49*C*C
从上面例子我们也可以看出3次3*3的卷积和在原图中一次7*7的卷积结果感受野是一样的
并且第一张图中的A的感受野为(3*3),B的感受野为(5*5),C的感受野为(7*7),随着深度的增加感受野越来越大，能看到的东西越来越多
2.可以增加网络深度
3.可以引入更丰富的非线性变换，使得网络可以拟合更多的可能性，更好地缓解过拟合；每次卷积都是一个非线性变换，引入更多的卷积核就会具有更多的非线性变换，引入更多的非线性变换描述能力也就越强。
参考文章
细说卷积神经网络（CNN）中所谓的“感受野”（Receptive Field）_cnn感受野_NorthSmile的博客-CSDN博客
