内旋(intrinsic rotations) = 旋转轴(rotated axis),右乘(R矩阵在右),应用于SLAM,机械臂运动学。

在新坐标系下,P点的坐标变为P′
外旋(extrinsic rotations) = 固定轴(也就是将坐标系下的所有点映射到新的坐标系下,求它们在新坐标系下的坐标),左乘(R矩阵在左),应用于机器人的姿态估计。
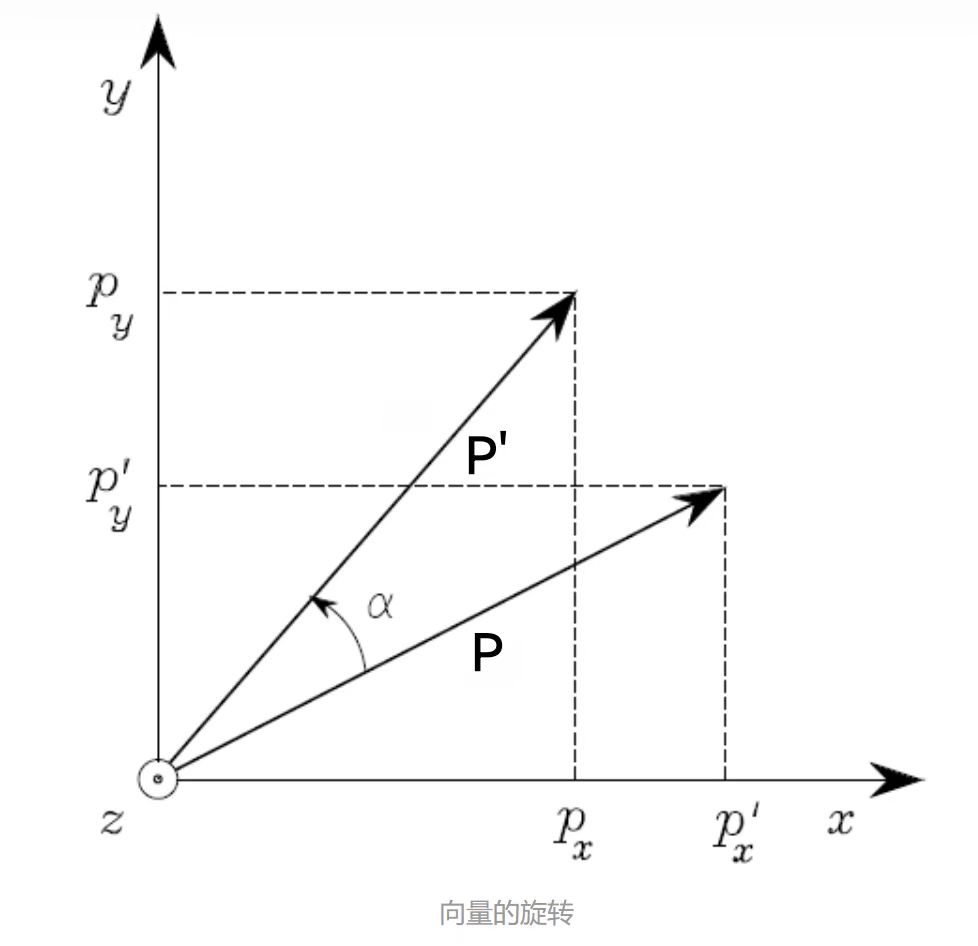
P点旋转α,得到新的点 P′
内旋与外旋的区别
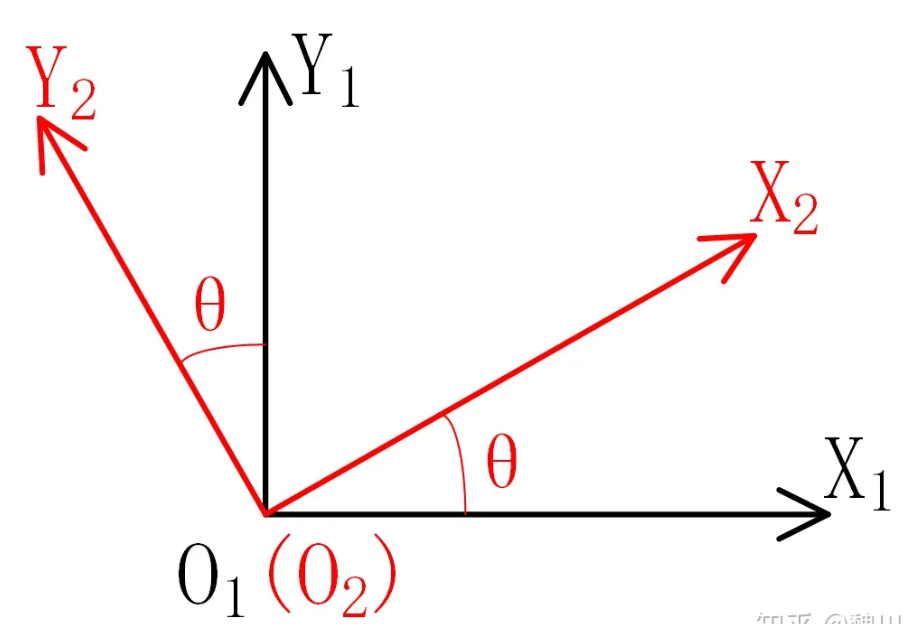
假设在世界坐标系中XYZ中存在物体,物体自身坐标系为xyz,假设初始状态物体相对XYZ的旋转为(0,0,0),即xyz与XYZ重合.我们定义旋转顺序为z->y->x,转角分别为γ,β,α。先绕z轴旋转γ,旋转过后,物体的x,y轴的坐标系发生了改变,z轴不变,得到新的物体自身坐标系x2y2z,此时的坐标轴x2,y2不再与世界坐标系的坐标轴XY重合。
内旋,外旋的区别在于:
在转β(第二个转角)时:内旋按照旋转后物体的坐标轴,也就是y2轴旋转,也就是说内旋按照动轴旋转。外旋按照世界坐标系中的Y轴旋转,外旋按照定轴旋转。旋转最后一个角度时亦然。
因此,我们描述一个能表示确定姿态/旋转的欧拉角,应该这样:
旋转角度(α,β,γ),旋转顺序(z->y->x),外旋。
或者:
旋转角度(α,β,γ),旋转顺序(x->y->z),内旋。
等等, 三个元素缺一不可。
其实一般我们用欧拉角是为了方便主观理解,最终我们一般还是要转换为旋转矩阵,或者四元数来参与计算。
欧拉角与旋转矩阵
旋转角度(α,β,γ),旋转顺序(z->y->x),外旋。
可以写为:
![]()
P'=RP
其中:
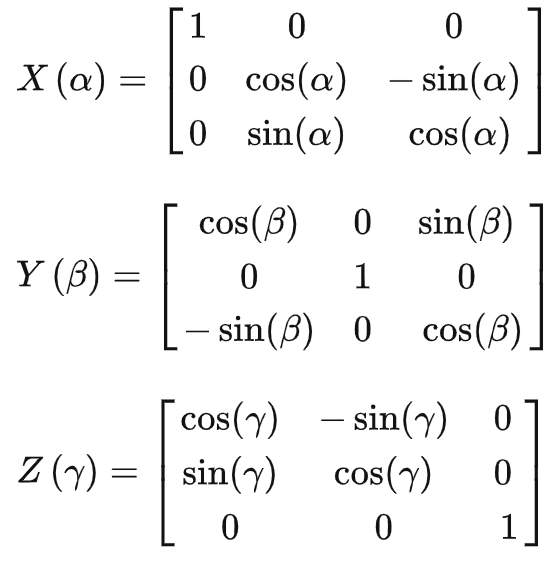
-----------------------------------------------------------------------------------
备注:
我们以外旋为例推导上述矩阵


旋转角的正方向由右手螺旋定则给定(z轴朝外),上述角适合于锐角也适合于钝角
-------------------------------------------------------------------------------------
而上述(α,β,γ),旋转顺序(x->y->z),内旋,可以写为:
![]()
P'=PR
每种特定顺序的外旋等价于其相反顺序的内旋,也就是说x->y->z内旋和z->y->x外旋的整体R矩阵是一样的。
万向锁
第二次旋转时旋转了90度或则-90度会发生万向锁问题:也就是第一次和第三次旋转都是绕同一的向量(世界坐标系的轴)在旋转(内旋)

由上图可知第一次和第二次同方向
参考文章:
欧拉角细节/旋转顺序/内旋外旋 - 知乎 (zhihu.com)
旋转向量和罗德里格斯旋转矩阵
旋转向量也称为轴角,轴是指发生旋转所绕的那个轴,角是旋转的角度,轴是旋转向量单位化后的单位向量,角是旋转向量的模。
罗德里格斯旋转矩阵使用旋转向量描述:
![]()

其中K是指轴的反对称矩阵。
另一种描述方式
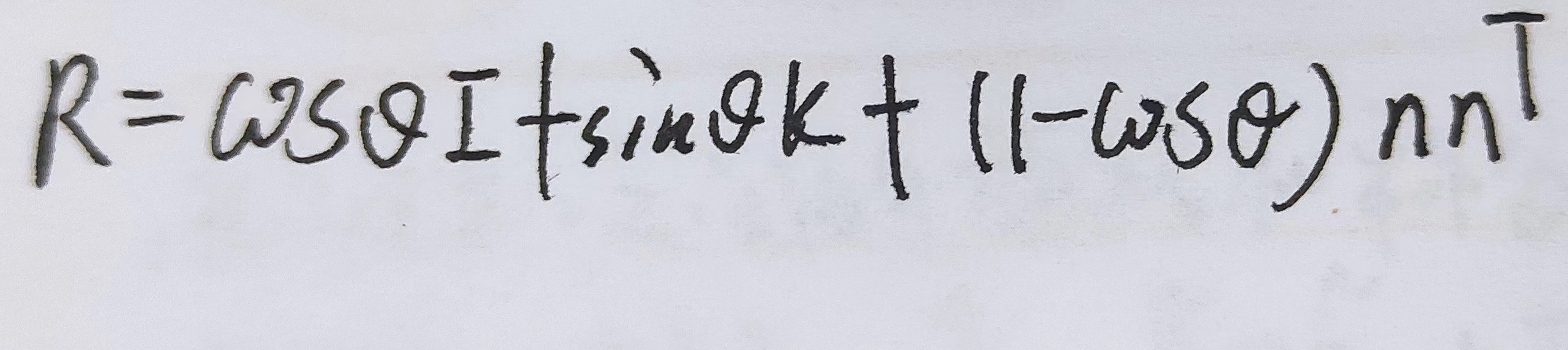
-------------------------------------------------
备注:
上述可以利用第一种描述方式加以下公式求得:
![]()
单位向量的二范数为1。
-------------------------------------------------
角度:
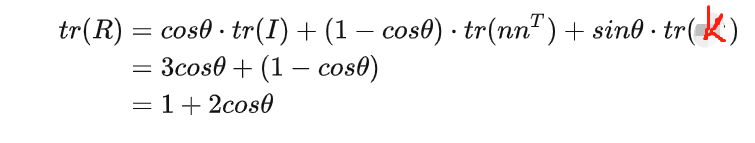

轴:
由于轴在旋转前后不发生改变则:
![]()
那么n为R中特征值为1的特征向量。





