栈:先进后出(子弹压樘),栈顶插入,栈顶删除,常见的应用是递归调用的实现
队列:先进先出(做核酸),队尾插入,队头删除
栈和队列顺序存储更为常见
栈
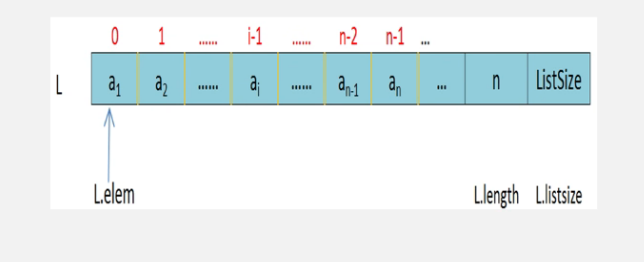
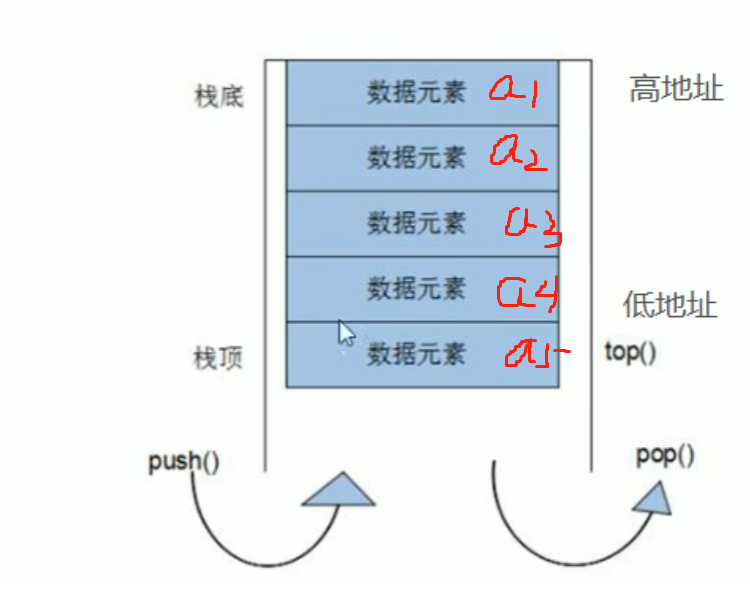
- 栈是向低地址增长的
- 不能遍历栈,因为只允许访问栈顶元素
- 每入栈一个元素栈的计数器就加1,因此可以求出栈的长度
栈的常用函数

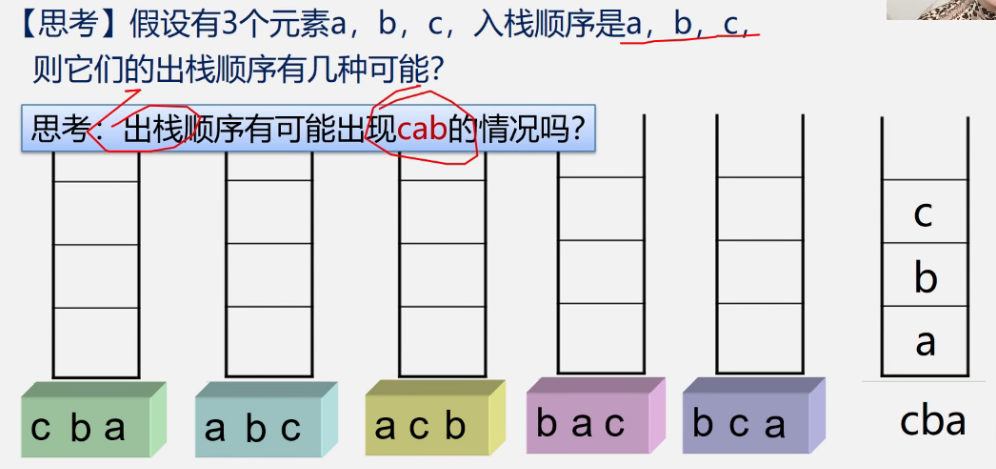
如果a和b紧挨着,b一定在a的左边
如果b和c紧挨着,c一定在b的左边
递归
递归是栈的应用,我们可以通过入栈和弹栈的过程来理解递归(先进后出)
递归的思想
递归的基本思想是某个函数直接或者间接地调用自身,这样原问题的求解就转换为了许多性质相同但是规模更小的子问题。求解时只需要关注如何把原问题划分成符合条件的子问题,而不需要过分关注这个子问题是如何被解决的。
递归的缺点
递归的缺点,从上图我们可以看出
在程序执行中,递归是利用堆栈来实现的。每当进入一个函数调用,栈就会增加一层栈帧,每次函数返回,栈就会减少一层栈帧。而栈不是无限大的,当递归层数过多时,就会造成栈溢出的后果。显然有时候递归处理是高效的,比如归并排序;有时候是低效的,比如数孙悟空身上的毛,因为堆栈会消耗额外空间,而简单的递推不会消耗空间。
递归的程序特性
优雅性
相比其他解法(比如迭代法),使用递归法,你会发现只需少量程序就可描述出解题过程,大大减少了程序的代码量,而且很好理解。递归的能力在于用有限的语句来定义对象的无限集合。
反向性
由于递归调用程序需要维护调用栈,而栈(我们在上文提过)具有后进先出的特征,因此递归程序适合满足取反类需求。我们在第五部分有一些编程实践,比如字符串取反,链表取反等相关有趣的算法问题。
递推关系(f(n)可以由f(n-1)或则f(n-2).....来表示)
递归程序可以较明显的发现递推关系,反过来也可以这么说,具有递推关系的问题基本都可以通过递归求解(当然也许有性能更佳的解法,但递归绝对是一种选择)。递推关系常见问题有杨辉三角、阶乘计算
什么时候用递归
说了那么多,那么我们什么时候可以用、应该用递归呢?
具有以下特征的问题可考虑递归求解:
当问题和子问题具有递推关系,比如杨辉三角、计算阶乘(后文讨论)。
具有递归性质的数据结构,比如链表、树、图。
反向性问题,比如取反。
总结下来,最根本的还是要抓住问题本身是否可以通过层层拆解到最小粒度来得解。
书写一个递归调用代码
1.递归的终止条件
判断当满足什么条件时我们直接终止语句不用运行程序,比如阶乘问题当n=1时我们直接返回1,比如二叉树的遍历如果我们遍历的是一个空树我们就不必遍历了。
2.非递归非终止条件部分
也就是想想如果递归只执行一次会执行哪些内容
3.找到递归的逻辑
也就是想想当前所研究的问题如何拆解成性质相同但是规模更小的问题,比如求5的阶乘我们可以求4的阶乘再乘以5,二叉树问题一个二叉树的左子树和右子树本身也是一个树
注意这里面2和3可以调换,2可以没有。
例子:实现二叉树的先序遍历
首先定义一个二叉树的结点
1 struct Node { 2 int data_; 3 //left 指向左子节点的指针 4 //right 指向右子节点的指针 5 Node* left; 6 Node* right; 7 Node(int data) :data_(data), left(nullptr), right(nullptr) {} 8 };
递归终止条件:
宏观了看:当一个树为空树,我们就不必遍历了
1 if (node == nullptr) { 2 return; 3 }
非递归非终止条件部分:
如果只有一个结点直接将结点装进容器中就好了
1 //非终止条件,非递归入口,只需考虑如果只有一个结点需要做什么 2 vec.push_back(node->data_);
找到递归的逻辑:
整个树的遍历我们可以拆分成先将根节点装进容器中然后对左子树的前序遍历再对右子树的前序遍历
1 //递归入口的参数是,性质相同但是规模更小的子问题,比如左子树它本身就是一个树但是相对于整个树而言它是一个规模更小的子问题 2 frontfind(node->left,vec); 3 frontfind(node->right,vec);
整体代码:
1 void frontfind(Node* node, vector<int>& vec) { 2 if (node == nullptr) { 3 return; 4 } 5 //非终止条件,非递归入口,只需考虑如果只有一个结点需要做什么 6 vec.push_back(node->data_); 7 //递归入口的参数是,性质相同但是规模更小的子问题,比如左子树它本身就是一个树但是相对于整个树而言它是一个规模更小的子问题 8 frontfind(node->left,vec); 9 frontfind(node->right,vec); 10 }
整体实现逻辑:



中序遍历就是,先对左子树中序遍历,然后装根节点,然后对右子树进行中序遍历
后序遍历就是,先对左子树中序遍历,然后对右子树进行中序遍历,然后装根节点
例子:阶乘
终止条件:
如果我实现的是1的阶乘,那么我直接将1返回就好了,至此程序就完成了
1 if (n == 1) { 2 return 1; 3 }
非递归非终止条件部分:
递归执行到1的时候可以将1直接输出,以上代码已经实现
找到递归的逻辑:
想实现n的阶乘可以用n*n-1的阶乘实现,想实现n-1的阶乘可以用n-1*n-2的阶乘实现
1 return n * fun(n - 1);
递归总结
现在,我们更加相信递归是一种强大的技术,它使我们能够以一种优雅而有效的方式解决许多问题。同时,它也不是解决任务问题的灵丹妙药。由于时间或空间的限制,并不是所有的问题都可以用递归来解决。递归本身可能会带来一些不希望看到的副作用,如栈溢出。
有时,在解决实际问题时乍一看,我们并不清楚是否可以应用递归算法来解决问题。然而,由于递归的递推性质与我们所熟悉的数学非常接近,用数学公式来推导某些关系总是有帮助的,也就是说写出递推关系和基本情况是使用递归算法的前置条件。
只要有可能,就应用记忆化。在起草递归算法时,可以从最简单的策略开始。有时,在递归过程中,可能会出现重复计算的情况,例如斐波纳契数(Fibonacci)。在这种情况下,你可以尝试应用 Memoization 技术,它将中间结果存储在缓存中供以后重用,它可以在空间复杂性上稍加折中,从而极大地提高时间复杂性,因为它可以避免代价较高的重复计算。
当堆栈溢出时,尾递归可能会有所帮助。
使用递归实现算法通常有几种方法。尾递归是我们可以实现的递归的一种特殊形式。与记忆化技术不同的是,尾递归通过消除递归带来的堆栈开销,优化了算法的空间复杂度。更重要的是,有了尾递归,就可以避免经常伴随一般递归而来的堆栈溢出问题,而尾递归的另一个优点是,与非尾递归相比,尾部递归更容易阅读和理解。这是由于尾递归不存在调用后依赖(即递归调用是函数中的最后一个动作),这一点不同于非尾递归,因此,只要有可能,就应该尽量运用尾递归。
参考文章:
(105条消息) 递归详解——让你真正明白递归的含义_是一只派大鑫的博客-CSDN博客
队

只有队头和队尾才能被访问,不允许有遍历的行为




