目的:
确定一条线或一个圆一个圆心的方程
面临的问题:
在线上的点因为噪声偏离这条线。
其他线上的点(外点)影响这条线的拟合。
遮挡导致这条线的不连续。
总括
所有的点都属于这条线:最小二乘
有外点:RANSAC,鲁棒拟合
有好多其他的线:RANSAC,或则霍夫变换
最小二乘

最小二乘面临的问题:
- 如果直线垂直(可以认为垂直于x轴)没法描述点到线的纵向距离
- 原本不垂直的线可能经过图像的旋转变成垂直的线
- 不同角度拍摄之后点和线的相对关系发生了改变

全最小二乘法
为解决上述问题我们使用全最小二乘法,即让点到线之间的距离最小(点到线间的距离永远是不变的)


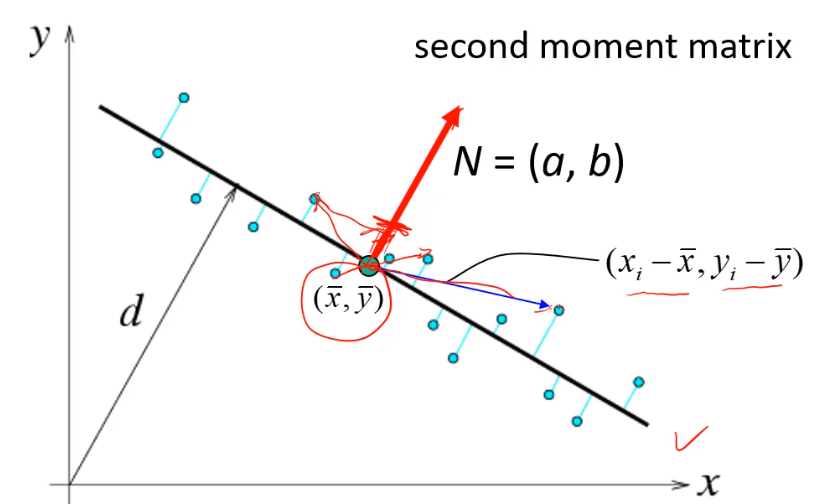
两个最小二乘的缺陷:
如下图所示,为了照顾外点(也就是那个偏离程度最大的点)必须拟合成红色的线,这会造成和蓝色的线有很大的偏差。
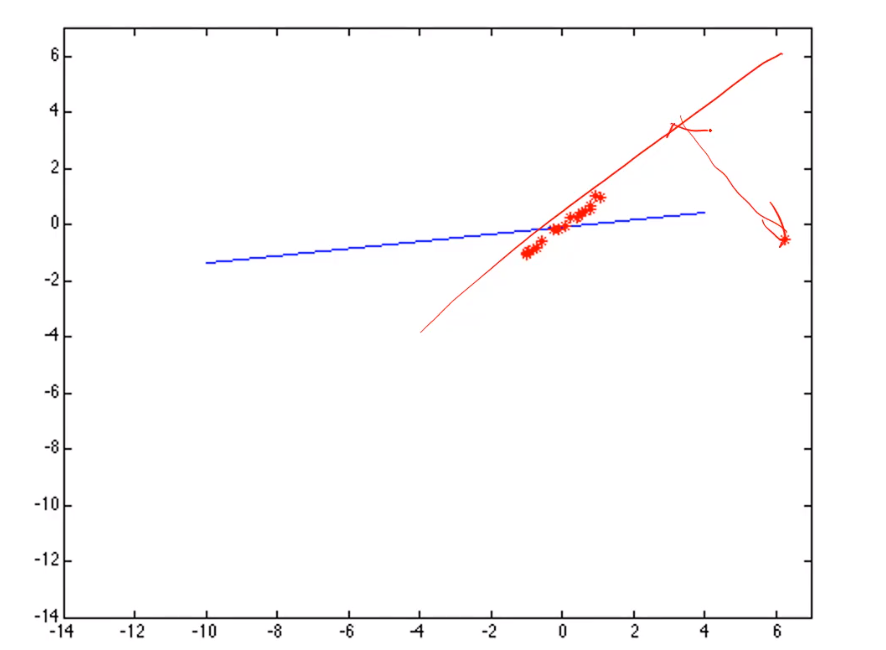
鲁棒的最小二乘:

此时E变成了非线性优化问题(看ρ的表达式),那么我们可以使用最优化的方法求解,我们可以使用全最小二乘法作为鲁棒的最小二乘法的初值。
鲁棒的最小二乘法问题:
σ太小极端情况所有点的距离都被看成1了,σ太大又变成上面的最小二乘问题了。一般取1.5倍的平均残差(残差就是点到线的距离)
RANSAC
首先要明白:RANSAC找到的是一个好的模型,而不一定是一个真实的模型,也就是RANSAC会认为哪条曲线的内点(以拟合直线为例,内点就是到这条直线的距离小于某一阈值的点)最多哪条就是一个好模型。
步骤:
- 首先随机选取n个点(比如直线的话选取两个点,圆的话选取3个点)
- 接下来以直线为例:
- 将这n个点拟合出来一个模型,比如两点确定一条直线
- 确定一个阈值
- 求其他所有点到这个直线的距离
- 记录下到这条直线的距离小于这个阈值的点的数目(如果此次拟合出来的模型是一个好的模型,那么这些点也称之为内点,只不过由于噪声的影响它们不在这条直线上了),这个数目我们可以称之为票数,至此完成一次迭代
- 接下来再选取两个点,再记录下票数
- 反复迭代得票数最多的那两个点确定的直线就是我们想要的直线
(圆的话三点可以确定一个圆,一个圆有它的圆心和半径,求其他所有点到圆心的距离,如果这个距离足够小小于某个阈值,我们可以认为是这个点投了一票)
使用在好模型上的内点确定迭代次数:

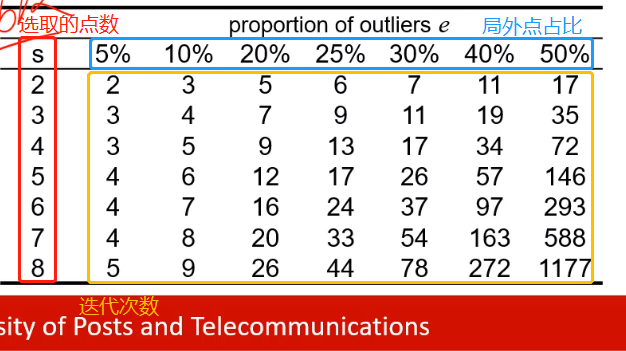
迭代停止条件:
我们可以一旦有一个模型的票数大于我们预先选择的阈值就停止迭代,我们也可以将迭代次数内所有大于阈值的直线都输出
自适应RANSAC
上面的内点数我们根本无法确定,不能先验,也就导致了迭代次数不确定,因此我们使用自适应RANSAC
步骤(以直线为例)
//初始化:
N=∞,sample_cout=0,k=0,s=2//Nk代表预计迭代的次数,sample_cout代表迭代了多少次
while Nk>sample_cout//随着sample_cout的增加,sample_cout会越来越逼近Nk,总有一次会等于Nk甚至会大于Nk
选择两个点,拟合出一条直线l,并且求出内点数,也就是点到线的距离为0的点数,根据内点数求出内点率带入下式
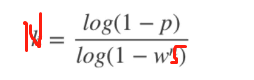
如果上述表达式求出的值比N小的话就用上面的表达式更新N值否则就保持N值不变,并且sample_cout++
————————————————————————
这里解释下为什么比N小就更新N
首先我们知道一个好的模型它的内点一定是相对较多的,因此我们就可以认为这个好模型的内点数就是真实的内点数,其所对应的迭代次数一定是一个合理的迭代次数。其次我们知道N一定是一个正值(分子和分母都是负的),因此N的绝对值越大,N就越大。内点数越多,w越大,ws越大,1-ws越小,分母的绝对值越大(注意分母分子始终为负值),又由于分子不变,因此N越小。
————————————————————————
当while跳出时我们得到的线就是最好的模型
当然有时我们有成百上千个点时,我们为了得到一个更快的算法,我们必须限制while循环次数,也就是当sample_cout达到某个值时我们就终止循环
其他
为了得到更好的模型,我们往往使用上述得到的好模型的内点利用全最小二乘法来拟合出个更好的模型
应用
RANSAC算法在指纹检测上的应用,以A为待比对的指针,看看B,C,D....哪个和它最匹配,图中只画出了B
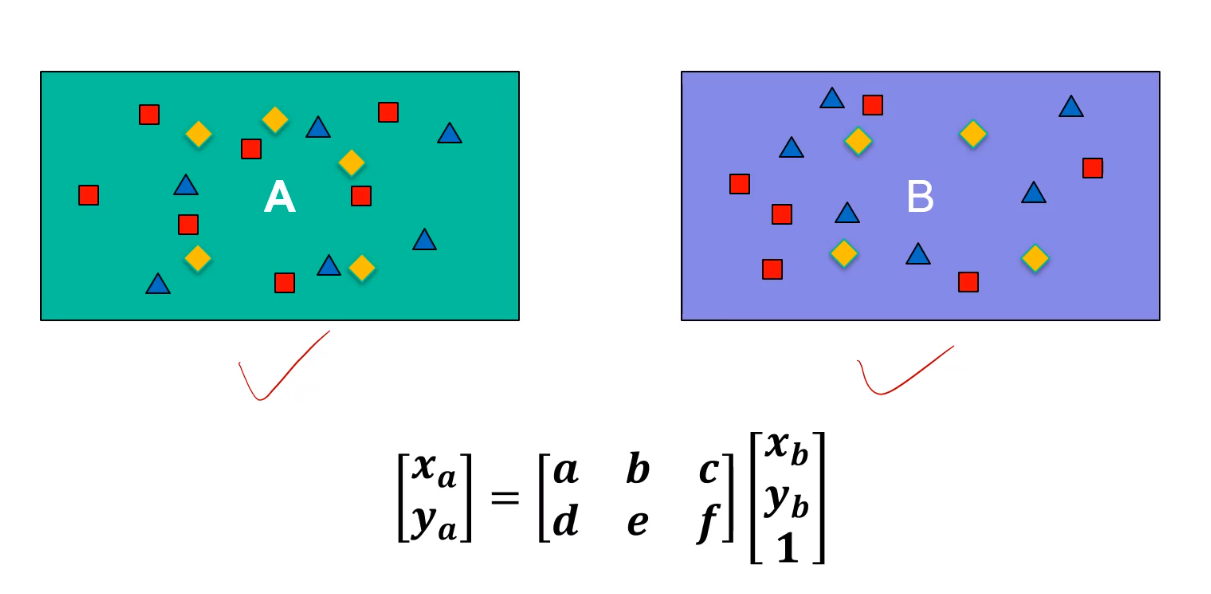
- 找出3对点(图中画出来的点),求出中间的矩阵设为T
- 然后用右侧所有剩下的点乘以这个矩阵T,以其中一个点为例,这个点乘以这个矩阵T后会对应到左图的一个坐标,如果这个坐标和左图中某点的距离小于我们设定的阈值,那么我们就认为右图中的这个点通过这个矩阵T找到了一个对应点,此时右图中这个点就给T矩阵打一分,类似的我们将其他所有点也这样做,就得到了这个T的最终分数。这样就完成了一次迭代。
- 我们再找到3对点,再求出T,再给这个T打分.......如此反复迭代我们得到了一个分数最高的T矩阵,以及通过分数我们也知道了右侧和左侧的匹配对数
- 我们接下来再拿一个图像C重复上面的过程,得到一个分数最高的T矩阵,以及通过分数我们也知道了右侧和左侧的匹配对数
比如B的最高得分是5分,它有5对点匹配上了;C的最高得分是12分,它有12对点匹配上了。我们要求得分数超过10的指针是和A所匹配的指纹,那么我们就可以知道C是和A匹配的指针,B不是。





