无穷远点(也称理想点)和无穷远线和无穷远平面
2D：
这个无穷只能在齐次坐标下表示，在欧式坐标系下并不方便
所有理想点都可以写成(x1,x2,0),并由比率x1:x2指定一个具体的理想点
直线的齐次表示：
性质1：
对于直线ax+by+c=0，我们可以用向量(a,b,c)T来表示，而且对于任何非零常数k直线ax+by+c=0和(ka)x+(kb)y+kc=0是同一条直线，因此(a,b,c)T和k(a,b,c)T也是同一条直线。
直线的方向向量和法向量：
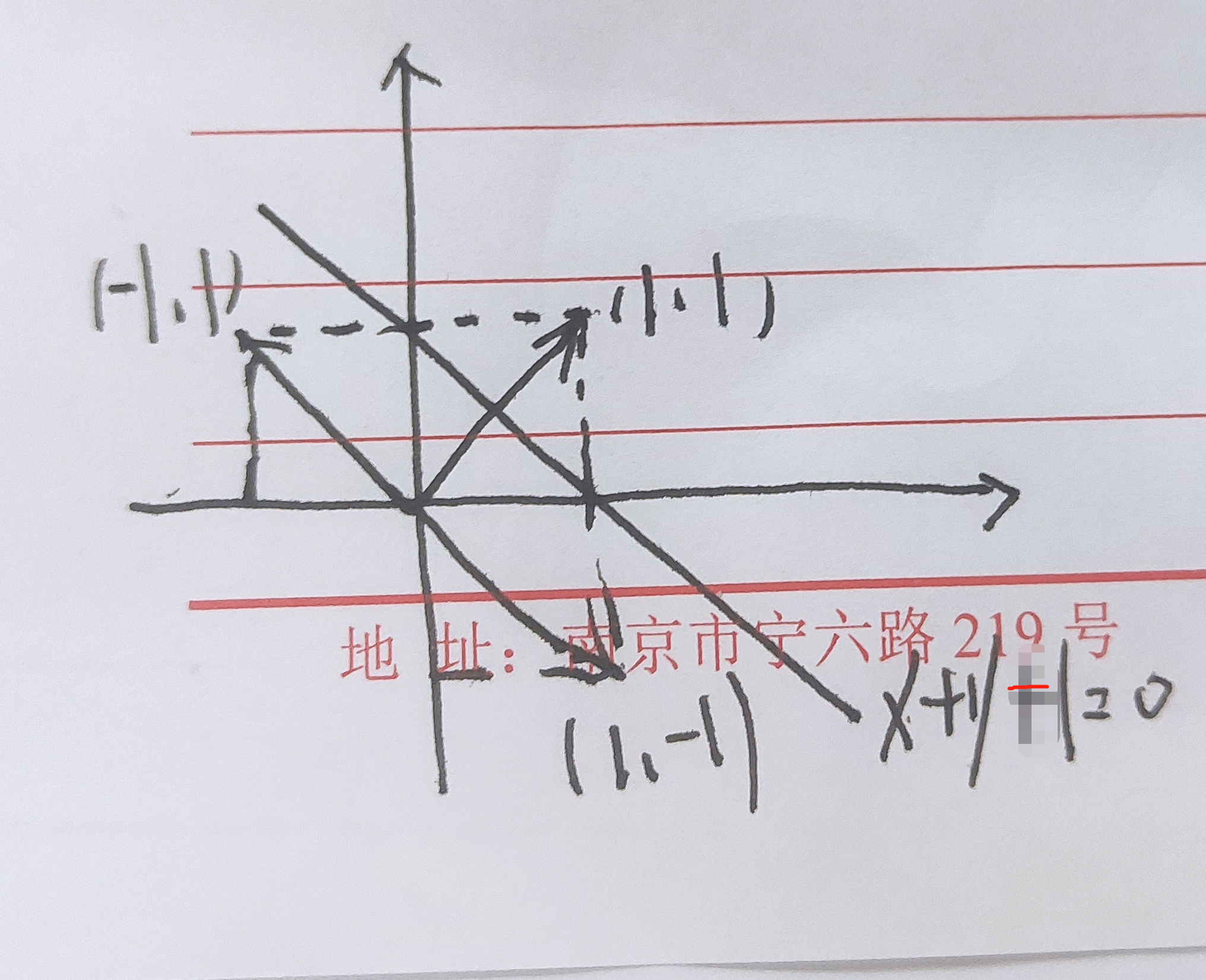
点在线上的表示形式：
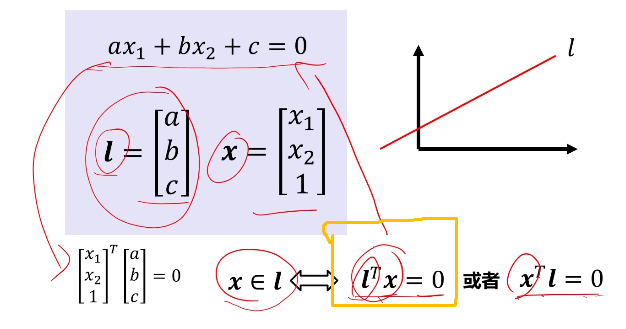
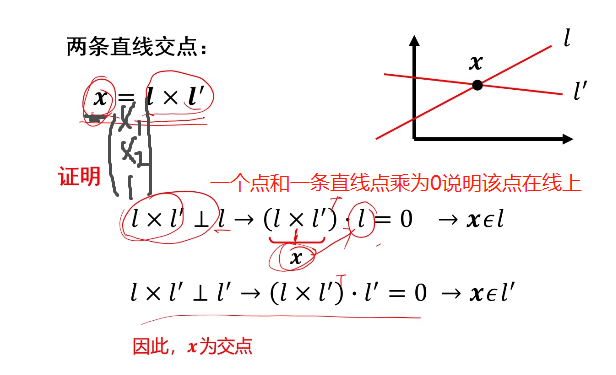
注意以上点都是齐次坐标
两条平行线的交点是无穷远点：
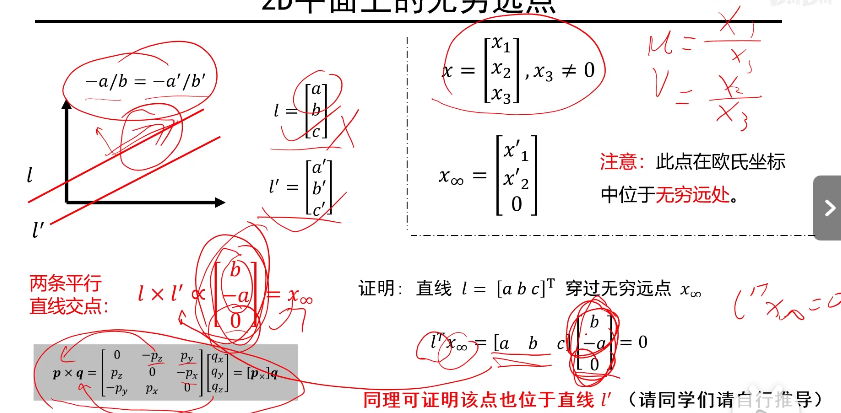
下面对于为什么是(b,-a,0)T做出解释:
此处用到了性质1
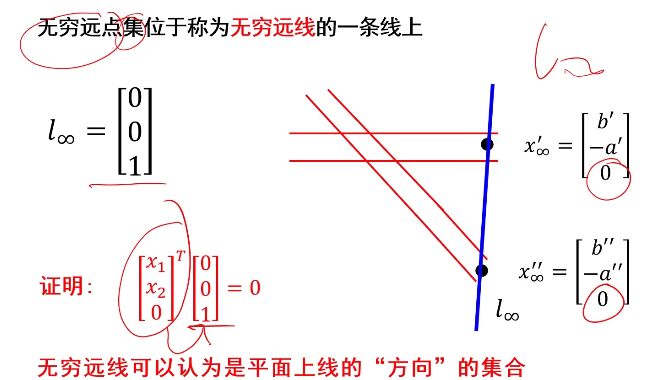
无穷远直线：
平行直线都会交于一个无穷远的点，所有无穷远的点会构成一条无穷远的线
3D:
点在面上：
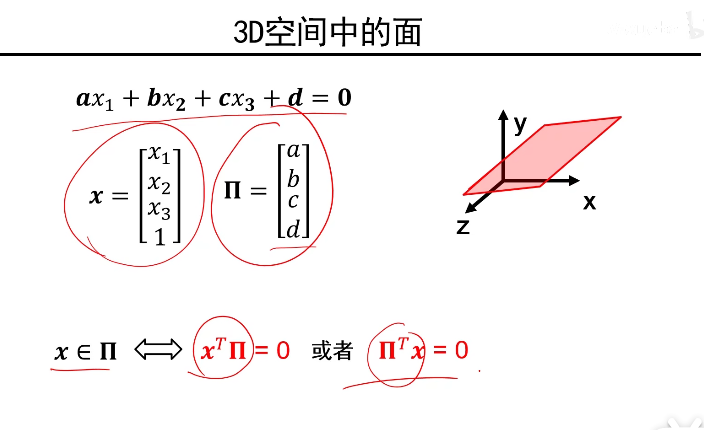
三维空间的直线：
首先注意的是Ax+By+Cz+D=0是面的方程，因此三维空间中的直线我们没法用方程表示，只能写出它的方向向量，记作(a,b,c)T注意这个地方和上面的参数a,b,c可不相同。那么两条直线的交线是(a,b,c,0)T再说一遍注意这个地方和上面的参数a,b,c可不相同.
无穷远面：
平行的平面都会交于一条无穷远线，所有的无穷远线的集合就是一个无穷远面。
或则说：
每一个平面都会对应一个无穷远线，平面上的所有点都会汇聚到这条无穷远线上，所有平行平面的无穷远线是同一根，所有无穷远线集合就是一个无穷点面。
用(0,0,0,1)T来表示
影消点和影消线：
点到点的映射
这个地方解释了仿射变换后平行性为什么不在保持：两条平行线交于无穷远点，而经过透视变换，两条平行线不再保持平行性，也就是不再交于无穷远点，交于我们可以看到的点，那么原来两条平行直线在无穷远处的交点经过透视变换就变成有穷远点，我们可以看见的点，也就是无穷远点不再是无穷远点。
而仿射变换保持了平行性：两条平行线在仿射变换后还是平行线，原来交于无穷远点还是交于无穷远点，因此无穷远点还是无穷远点。
也就是无穷远被保持意味着平行性也被保持。
线到线的映射
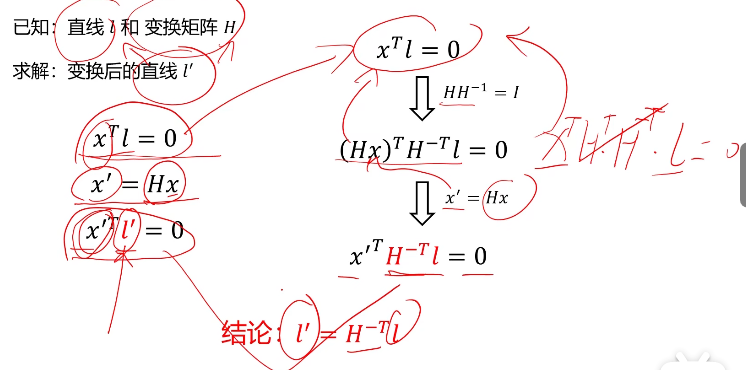
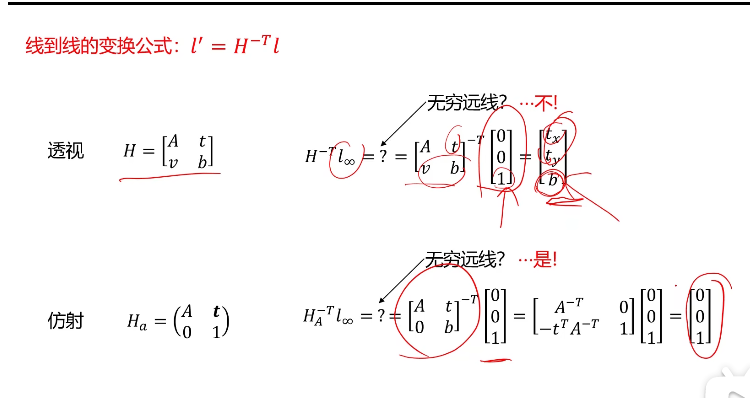
可以通过立体图形来理解，无穷远线被保持意味着无穷远面之间还是平行的
影消点：
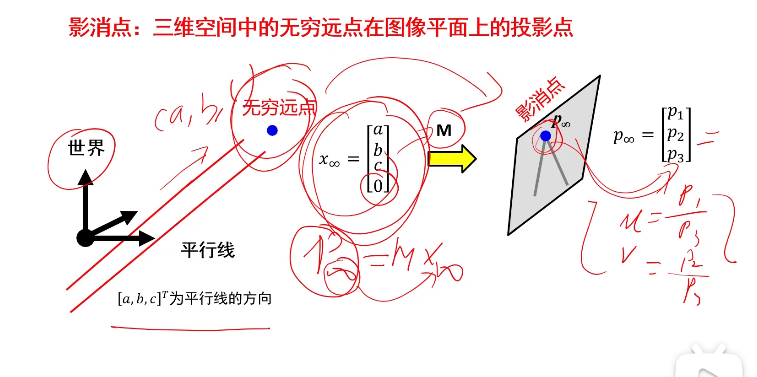
M是投影矩阵，是透视变换，p∞是像素坐标
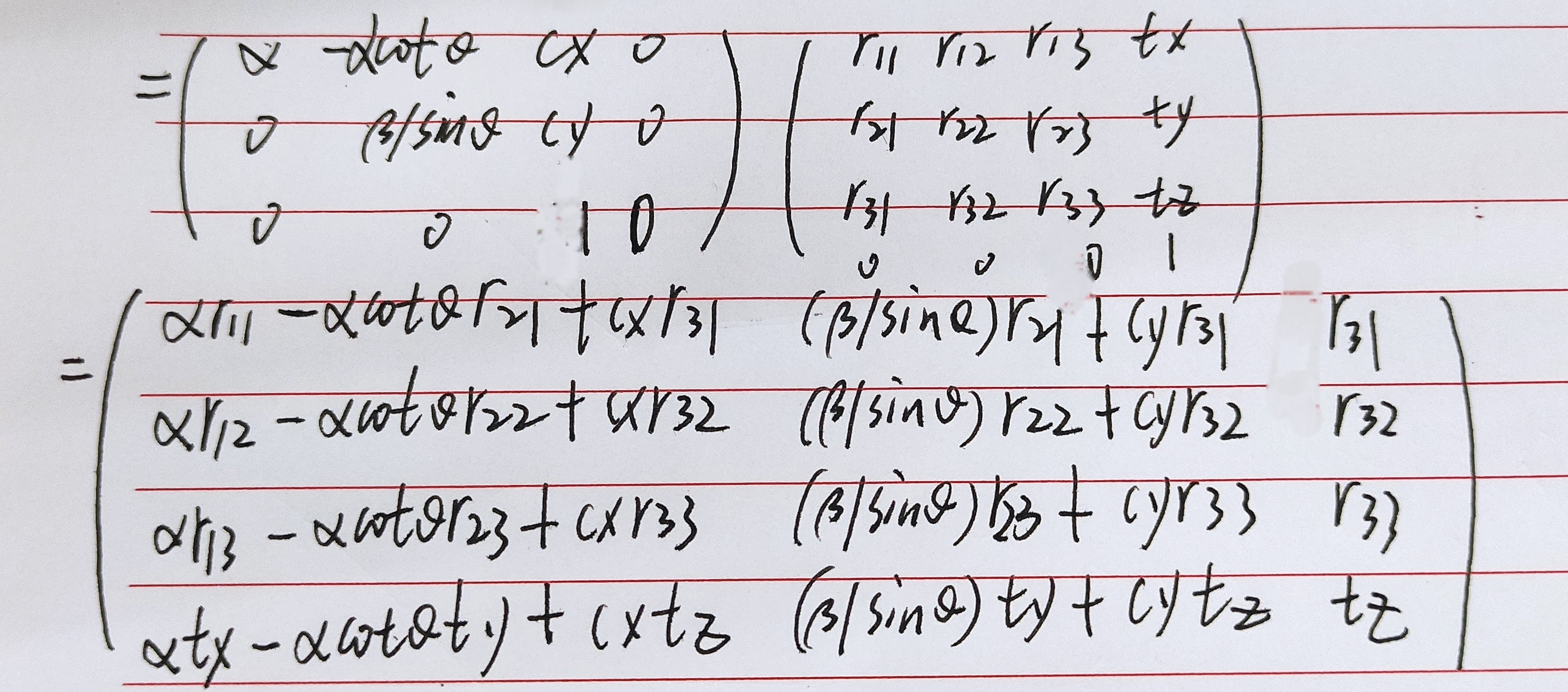
根据相机内参和直线的方向求直线的影消点：
黑色的d和红色的d是不一样的，黑色的d是一个单位向量，黑色d等号右边是对K-1v进行归一化处理(一个向量除以模等于单位向量)
K是相机内参，注意这里的直线方向是相机坐标系下的，因此不考虑外参矩阵
影消线
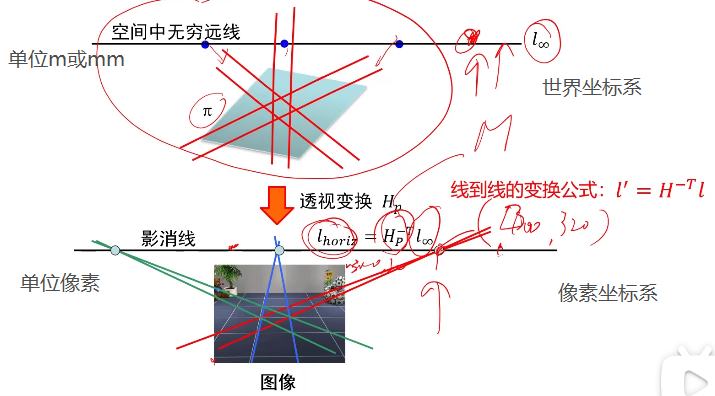
根据相机内参和平面的影消线求平面的法向量：
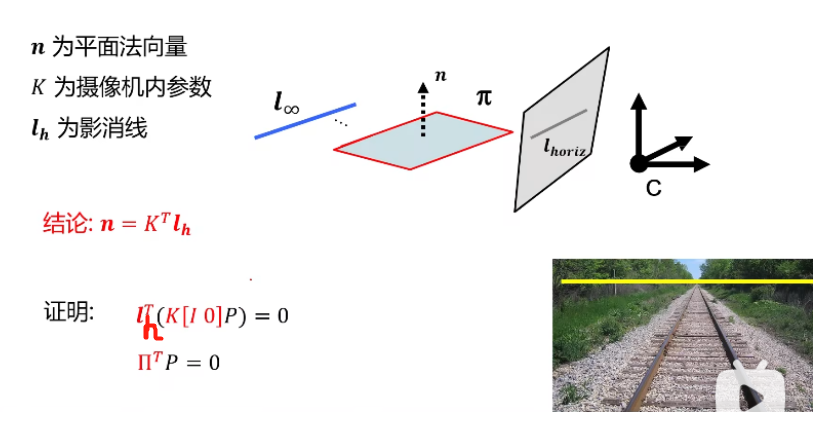
K[I 0]P的理解，也就是平面上的点在像平面上的点的投影为什么全部在影消线上：
个人理解是，无数条线组成面，而每条线上又有无数个点，这无数个点就是面上的点，而这无数个点在无穷远线上的对应点，是它们所在直线与无穷远线上的交点，那么这些点在像平面上的投影就是这个交点的投影，而这些投影点全部在影消线上，因此平面上的点在像平面上的投影全部在影消线上。但是当你只考虑空间平面和像平面的关系，如果空间平面和像平面不垂直的话那么空间平面的所有点在像平面上的投影点所组成的是一个平面而不是线那么lh的那个表达式好像又不成立
个人认为这样证明：
根据影消点的结论，空间中任意平面上的直线和它的影消点的关系为v=Kd,d为直线的方向。从而d=K-1v,因为平面上的任何一条直线都和平面的法线相垂直，因此dTn=vTK-Tn=0,n为平面的法向量也就是平面法线的方向，因为影消点在影消线上，假设一个平面的影消线为lh,则vTlh=0,因此lh=K-Tn，因此KTlh=n
两条直线的夹角：
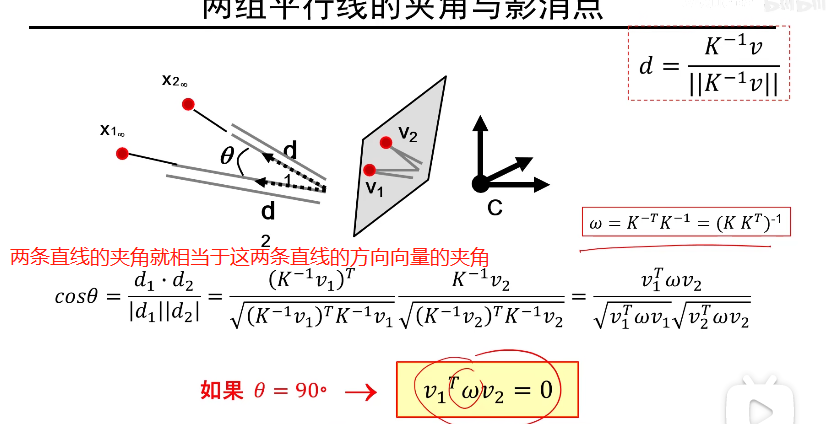
w的性质
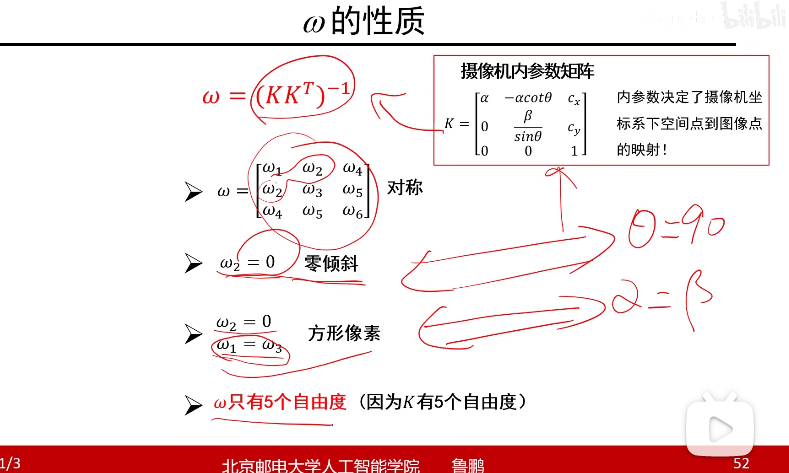
用张正友的标定方法来看，w2=0意味着γ=0，w1=w3意味着α=β，这样就是3个自由度
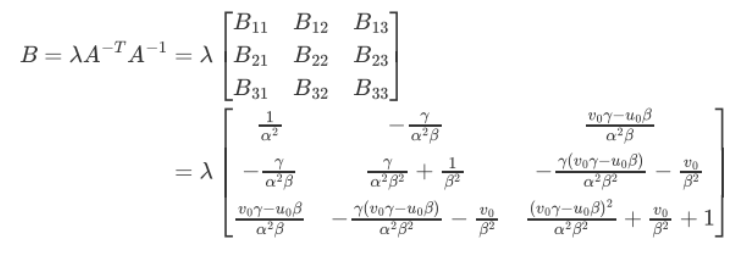
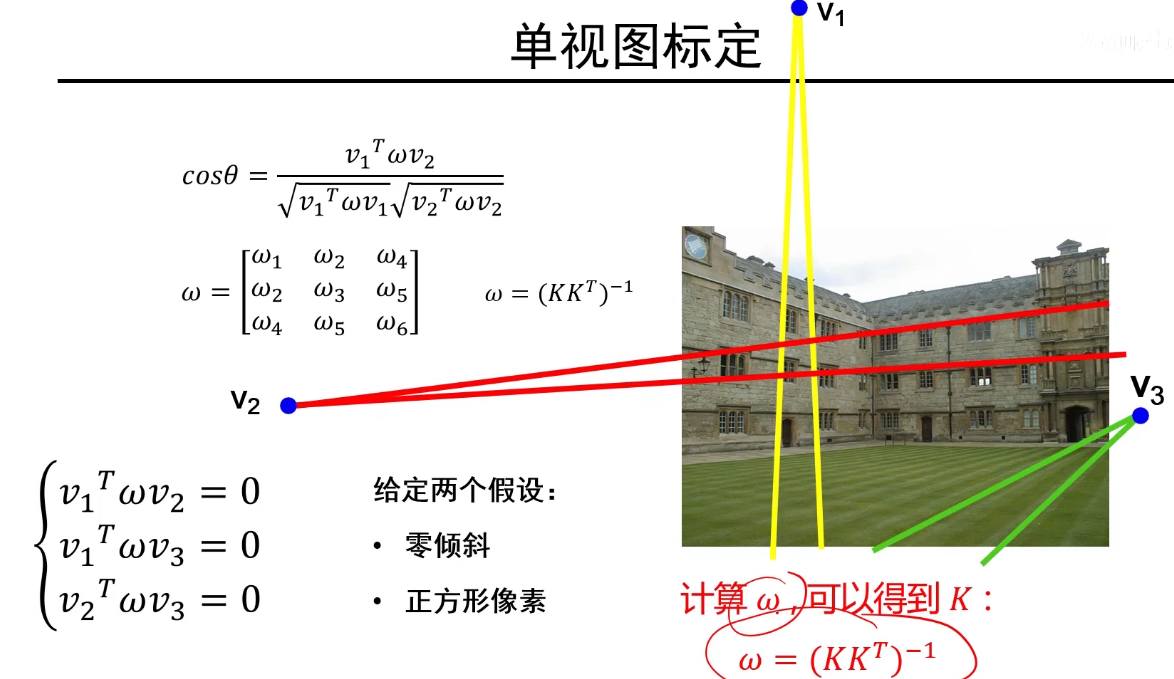
三个方程三个自由度
因此可以得到任意一个平面的法向量，因此从而可以构建出任意平面
个人认为的步骤：(灭点即为影消点)
- 首先找到图像中三个互相正交的平面。
- 然后在每个平面上找两个点，求出两点的像素坐标，然后将两点的像素坐标叉乘(lTx1=0说明l和x1垂直，lTx2=0说明l和x2垂直,那么l,x1,x2相互垂直)，求出两点所在的直线比如(a,b,c)，那么这个直线的灭点就是(b,-a,0)
- 分别在三个平面上找到一个灭点，建立三个方程求出内参矩阵
- 再在所求平面找到三个点(三点不能在同一条直线上)，求出它们的像素坐标，两两可构成一条直线，一条直线可对应一个灭点。两个灭点可以求出该平面的影消线，从而求出平面的法向量
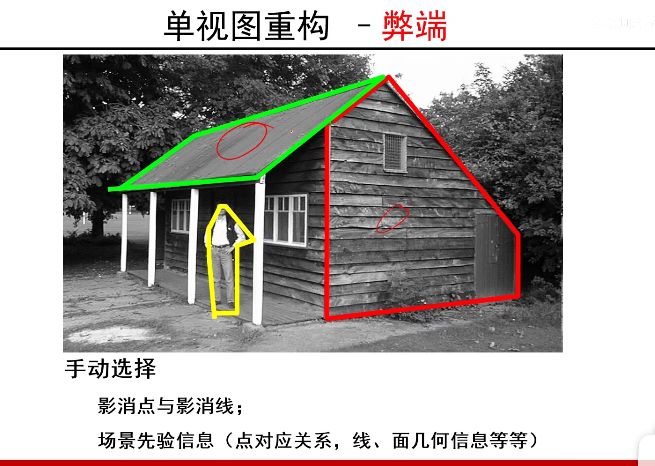
需要人为的选择平行线，并且单视图无法恢复深度信息。
