写在前面
首先要分清投影矩阵和单应矩阵
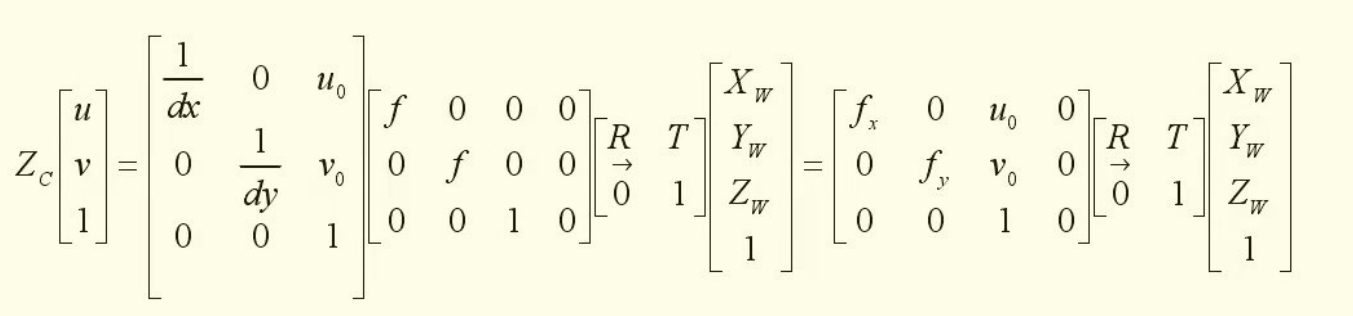
在上式中内参矩阵和外参矩阵相乘得到的是投影矩阵(3*4),它反应了三维点和二维点的关系。而张正友相机标定法使Zw=0使得世界坐标下所有角点处于同一平面,这样是二维点到二维点的映射,那么外参矩阵和内参矩阵相乘后第三列(下图框住那部分就是)因为Zw=0而没有参与运算,此时是单应矩阵(3*3)
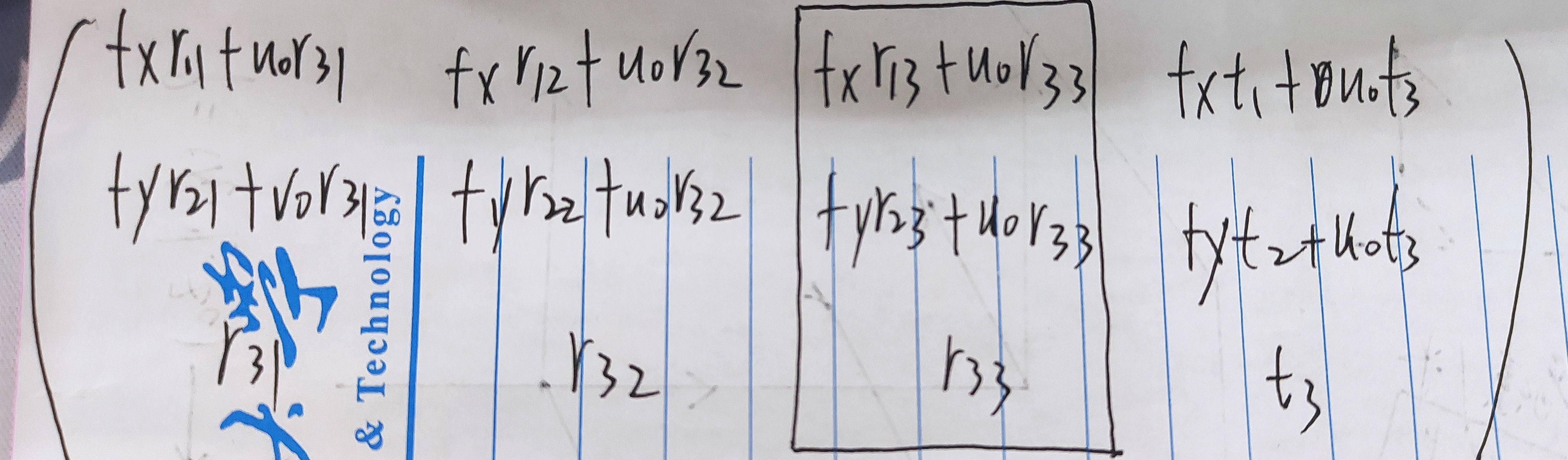
上图整个矩阵是投影矩阵,如果写成列向量的形式可以写成:(r1,r2,r3,t);如果去掉第三列为单应矩阵如果写成列向量的形式为(r1,r2,t)。
说明本文的内容来自不同地方的总结,因此符号没有做到统一,此处做下统一:
fx=α
fy=β
cx=u0
cy=v0
ρ=λ
注意图像压缩对各参数的影响:
图像压缩后图像的分辨率变小了,也就是像素点的个数变少了,那么像平面的大小不变,则每个像素点的物理尺寸变大了,那么dx和dy(表示一个像素的水平尺寸和竖直尺寸)就变大了。640*480->640*240
因为fx=f/dx,fy=f/dy,则fxfy变小了。
而压缩图像对于像平面的位置和光心并不会产生影响,那么主点的位置还是原来的位置(主点表示光轴与像平面交点,也就是图像坐标系的原点),而cxcy表示主点的像素坐标,像素变少了原来位置的主点的像素坐标也就变小了。
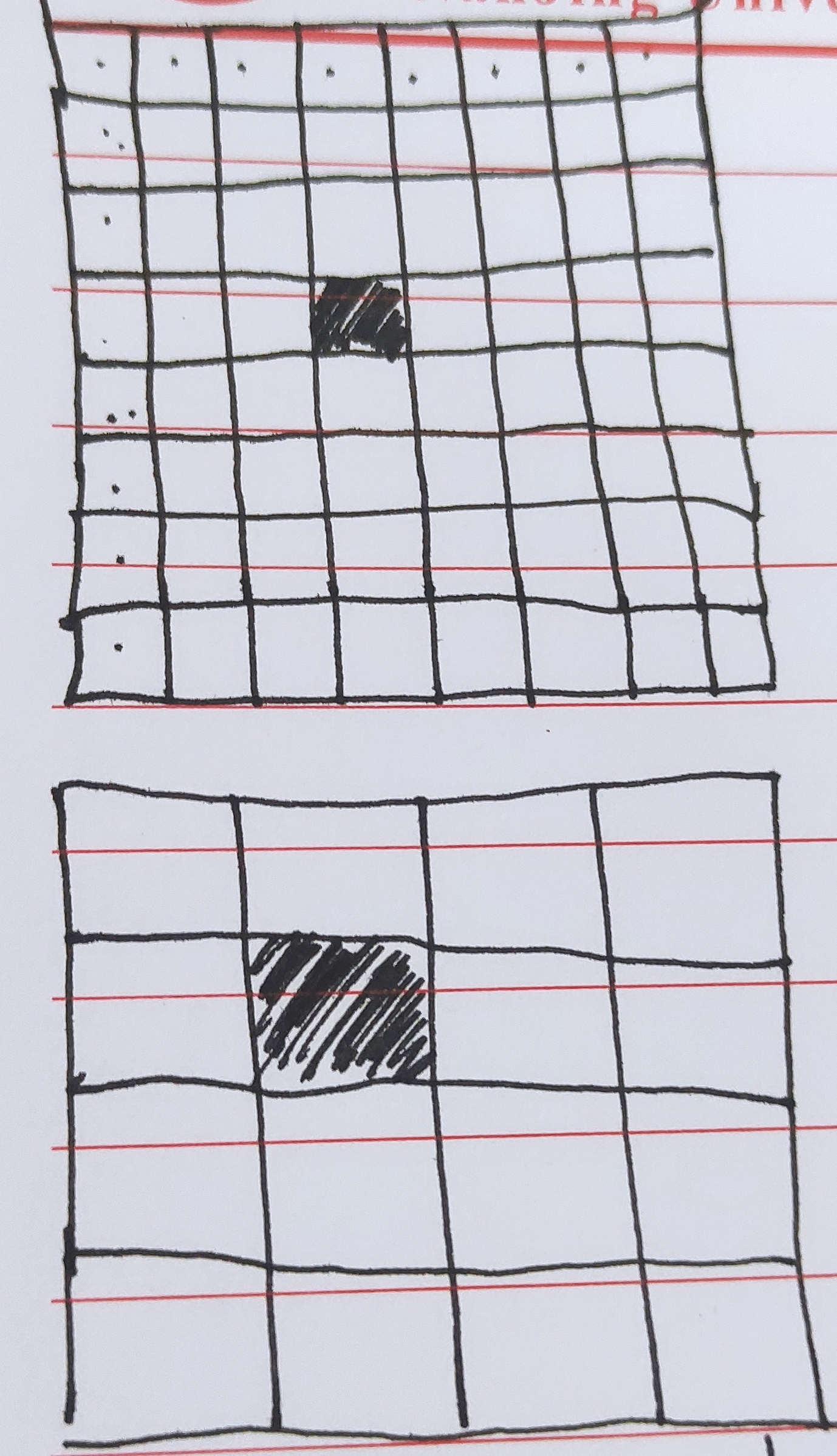
因此将640*480的图像压缩到320*240,那么fx,fy,cx,cy均变为原来的1/2
最本质的标定方法
当像素为正方形时的成像模型:

当然还是因为制造工艺问题像素可能不会为正方形,此时模型变为(角度是0到90度之间的):

关于像素形状的结论(这里面零倾斜就是像素为正方形的意思):


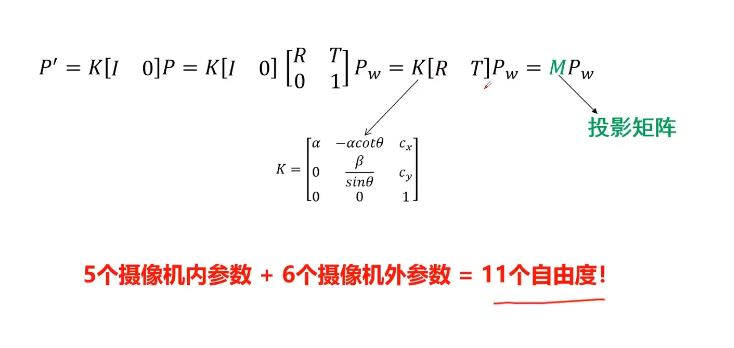
旋转有x,y,z三个自由度,平移也有x,y,z三个自由度
注意这个地方是齐次坐标系下的对应关系,如果根据世界坐标系求出像素坐标系下的点,想要求该点的欧式坐标还需要将u,v除以Zc,这样得到的u/Zc和v/Zc才是像素的欧式坐标
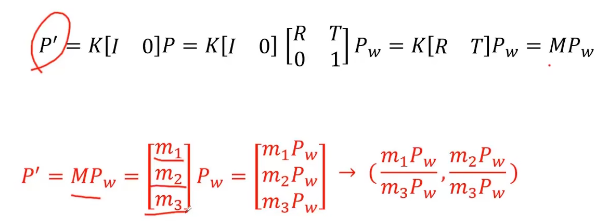
mi是1*4,Pw是4*1
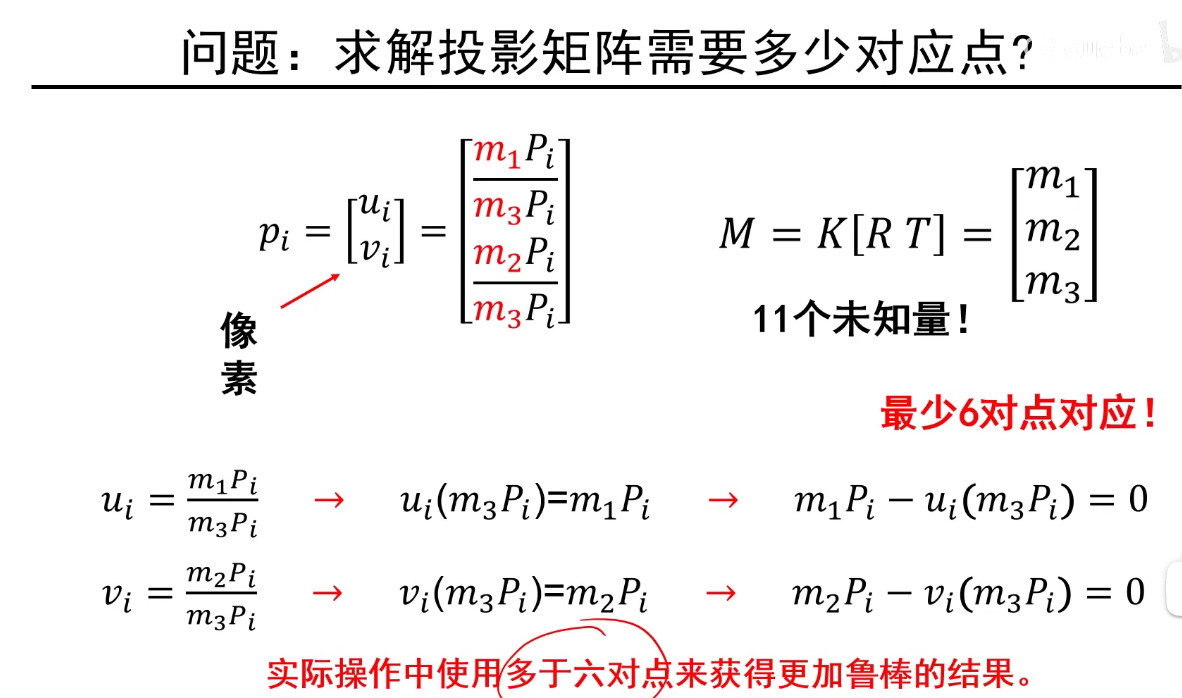
这里面原本应该是12个未知量但是因为最小二乘法使得m112+m122+m132+m142+m212+m222+....+m342=1因此相当于12个未知量中任意一个也可以由其他参数表示,因此是11个未知量,而最少要6对点构成12个方程。
将所有点构成的方程写在一起:



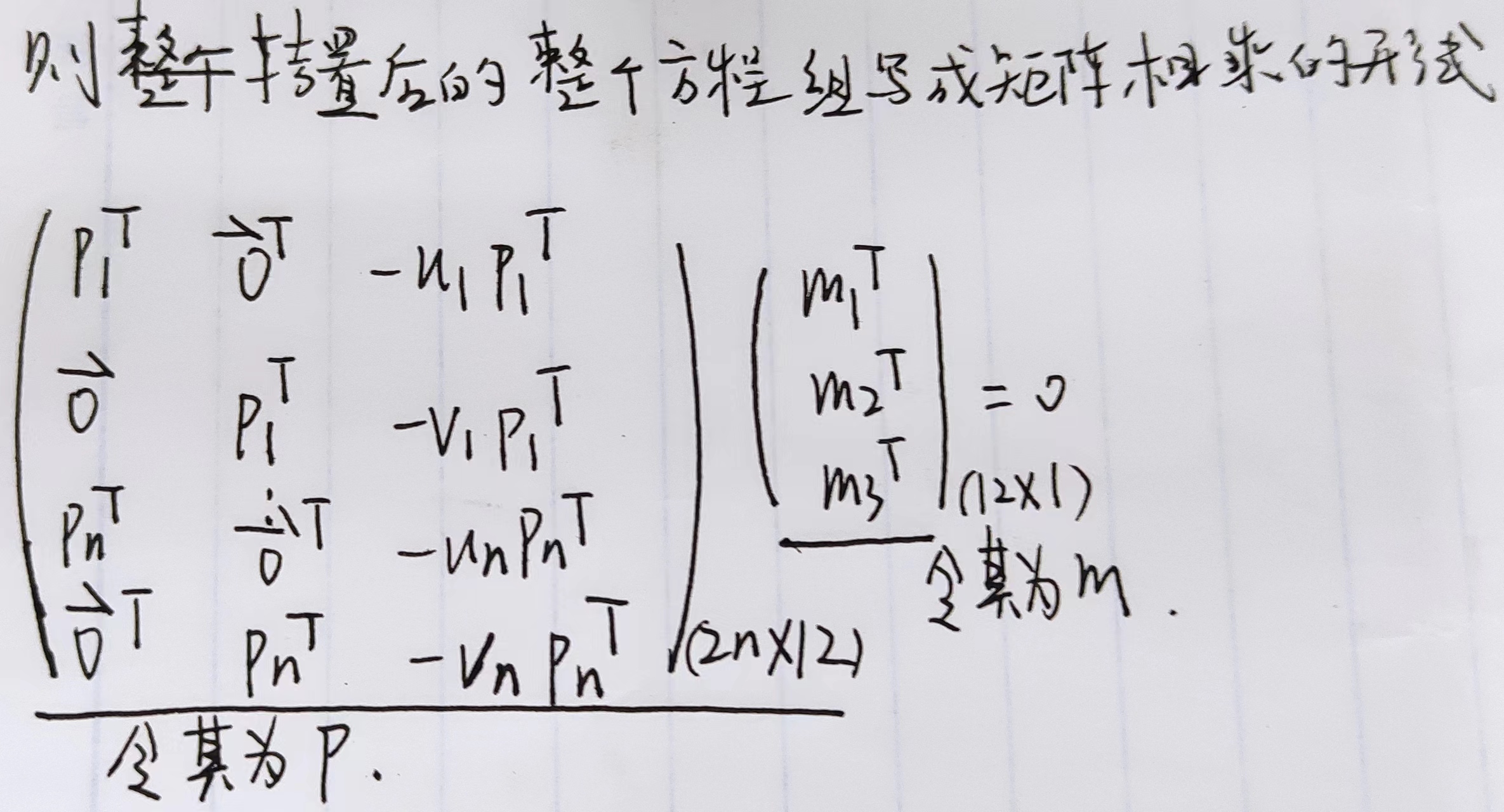
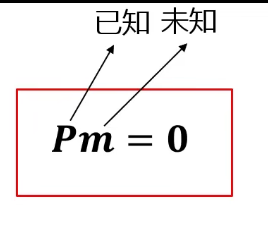
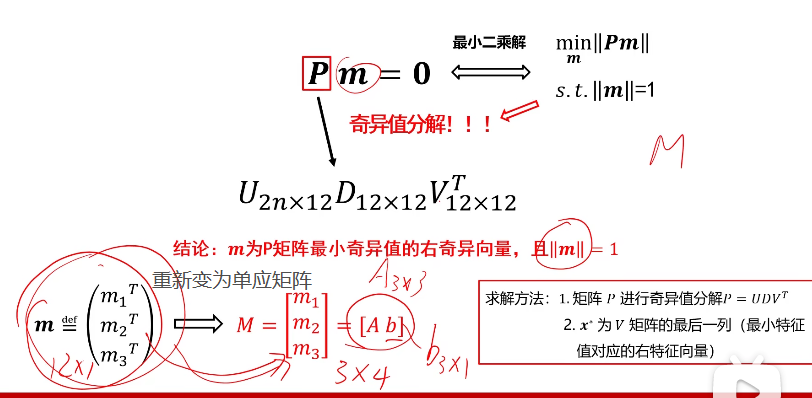
A和旋转矩阵相关,b和平移矩阵相关
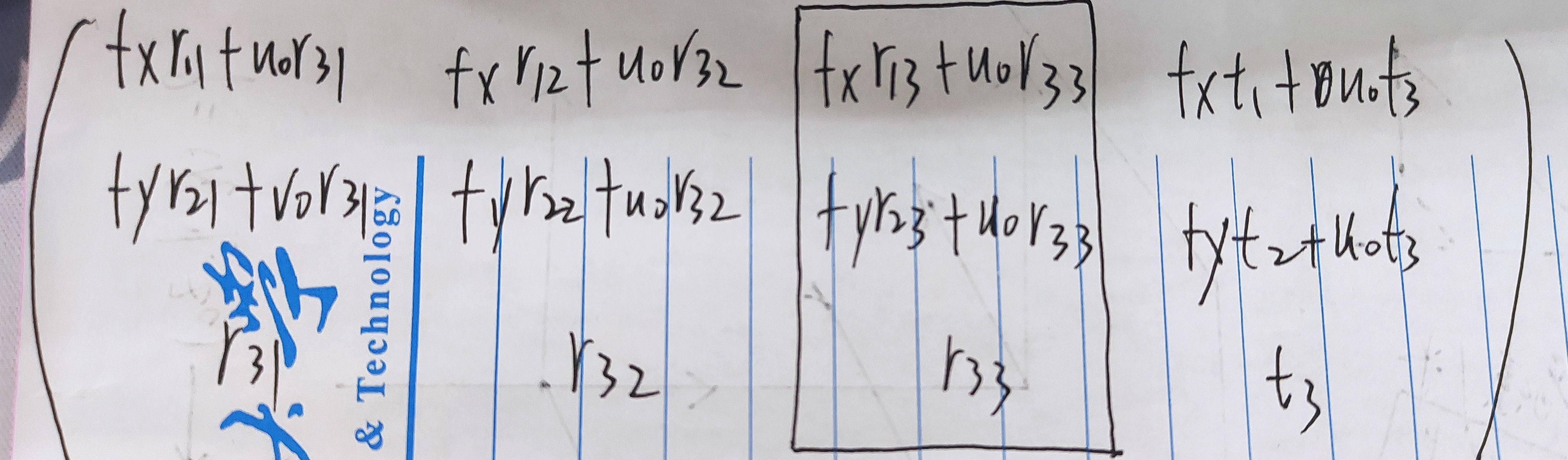
注意虽然我们带入的式真实的单应矩阵(下图的M)
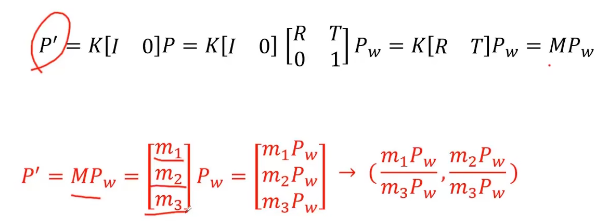
但是因为我们这里的单应矩阵式通过最小二乘法求出来的,要求||m||=1,因此单应矩阵和真实的单应矩阵相差一个比例系数。
最后整理可得:

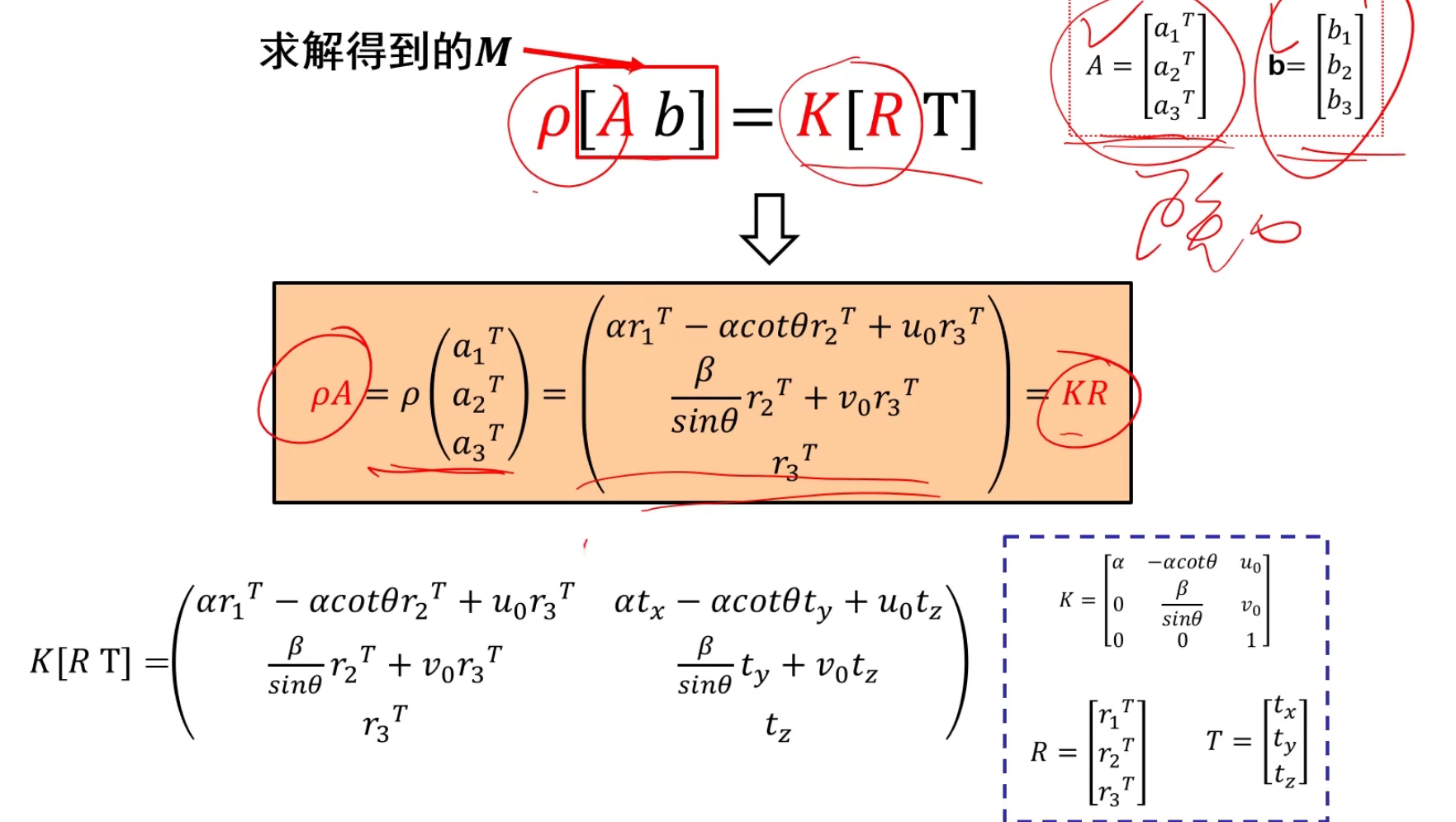
a1,a2,a3;r1,r2,r3都是列向量。
到目前为止我们已知了a1,a2,a3它们是根据最小二乘法求得的m的前三列向量
ρ,u0,v0的求解

这里面ρ的模相当于绝对值,因为不知道它的正负所以加一个±
角度的求解:

注意这里的角度是0到90度之间的
之所以是-αr2因为r1×r3=-r2,这里面是右手坐标系,如下图所示:
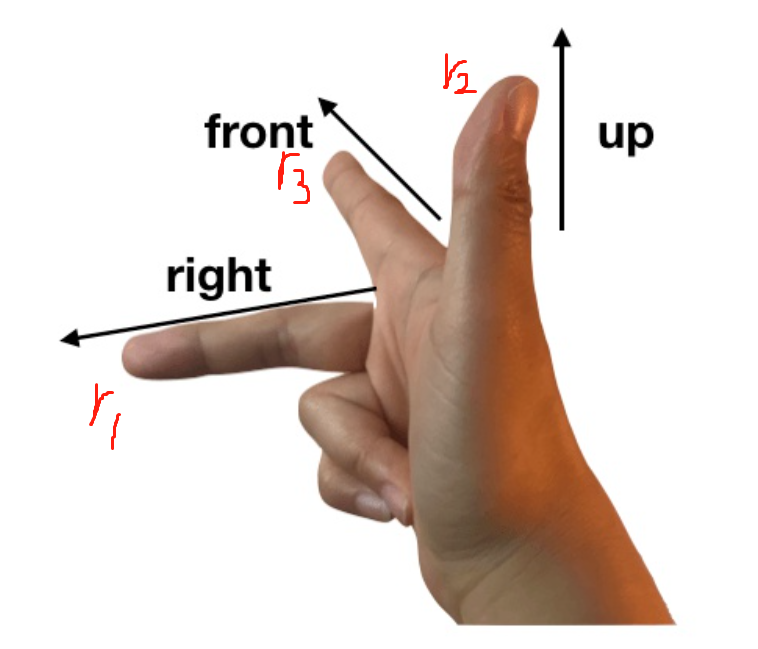
然后根据右手螺旋定则:


上式求解过程为

根据上式可知当角度为0时分母为0可以得到以前的一个结论:

α和β的求解

当α和β相等时又可以得到以前的一个结论:

外参的求解:
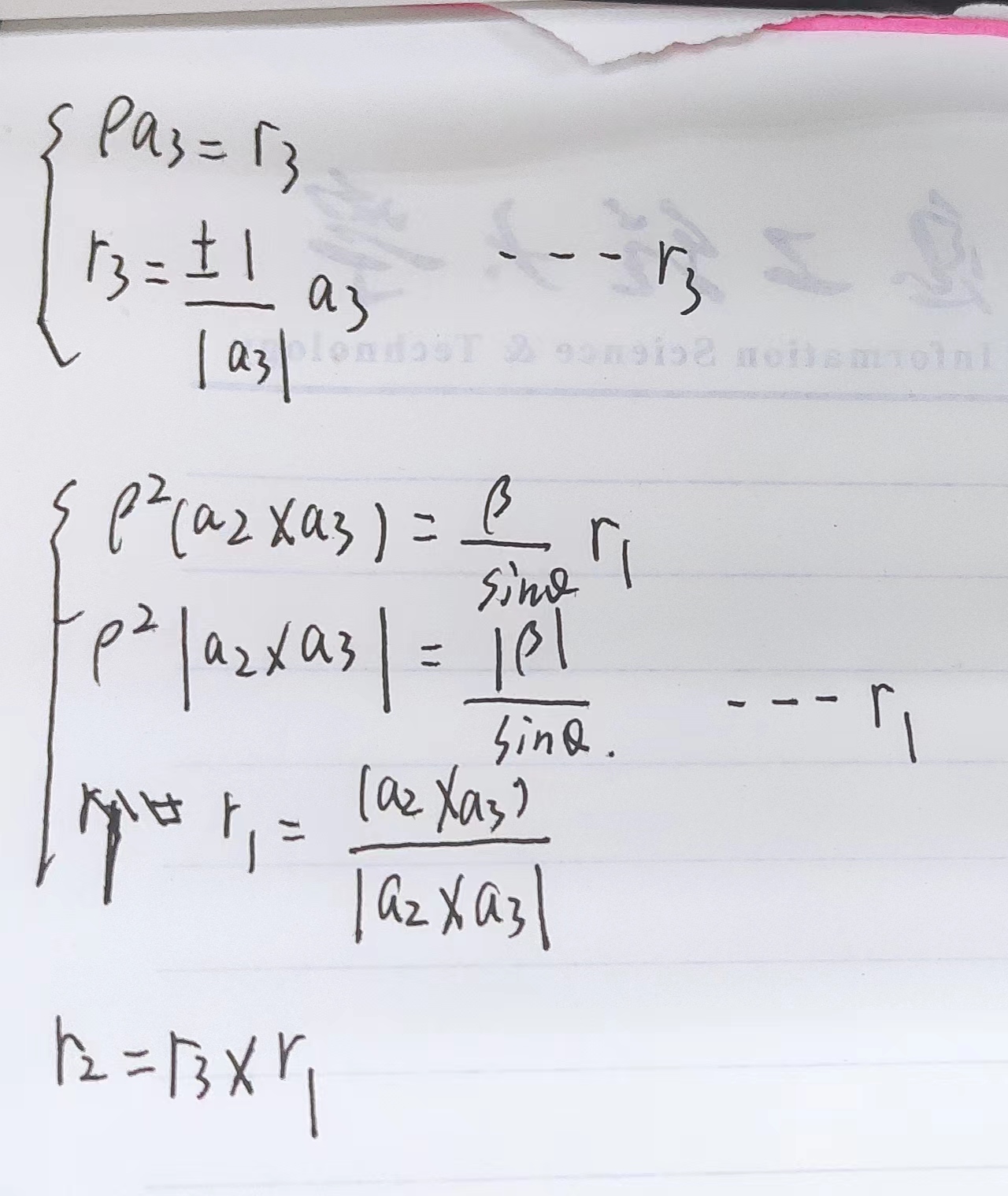
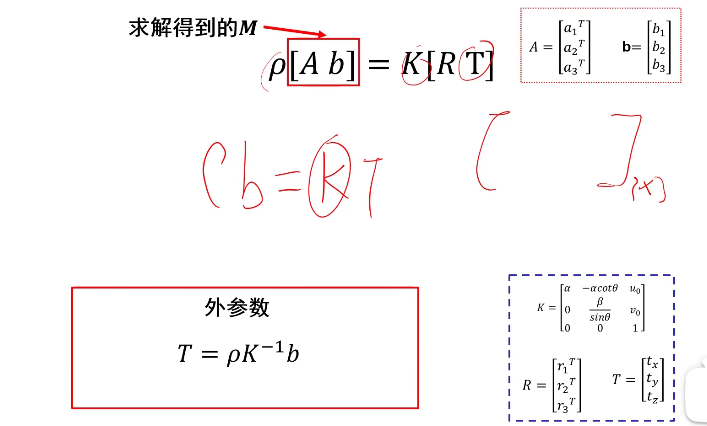
张正友相机标定法
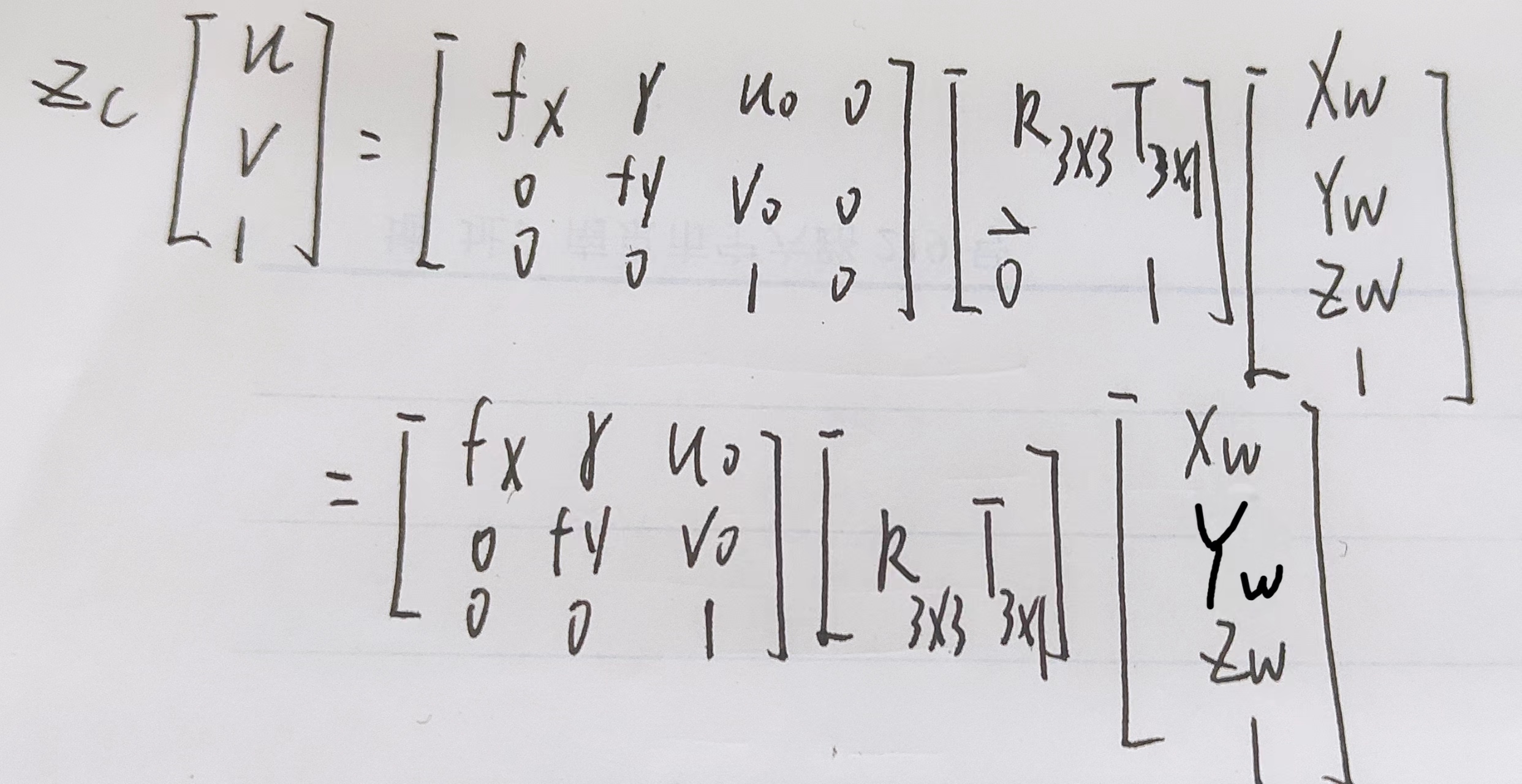
将上式简化,并规定棋盘格的左下角为世界坐标的原点,棋盘格的左上角为像素坐标的原点,这样棋盘格上所有的点都处于同一平面,此时ZW=0。
这里注意规定了世界坐标的原点后棋盘格上的任意角点的坐标就可以由长度确定,例如棋盘格的尺寸为5毫米,则左下角角点的右边那个角点坐标就是(5,0,0);同理像素坐标则按该角点是第几个像素来计算,例如该角点为第一行第一列的像素,则它的像素坐标为(1,1)。
由于ZW=0则:

———————————————————————————————————————————————————
备注:
这里面推下旋转矩阵的第三列(r3)为什么没了,也就是单应矩阵怎么得到的:
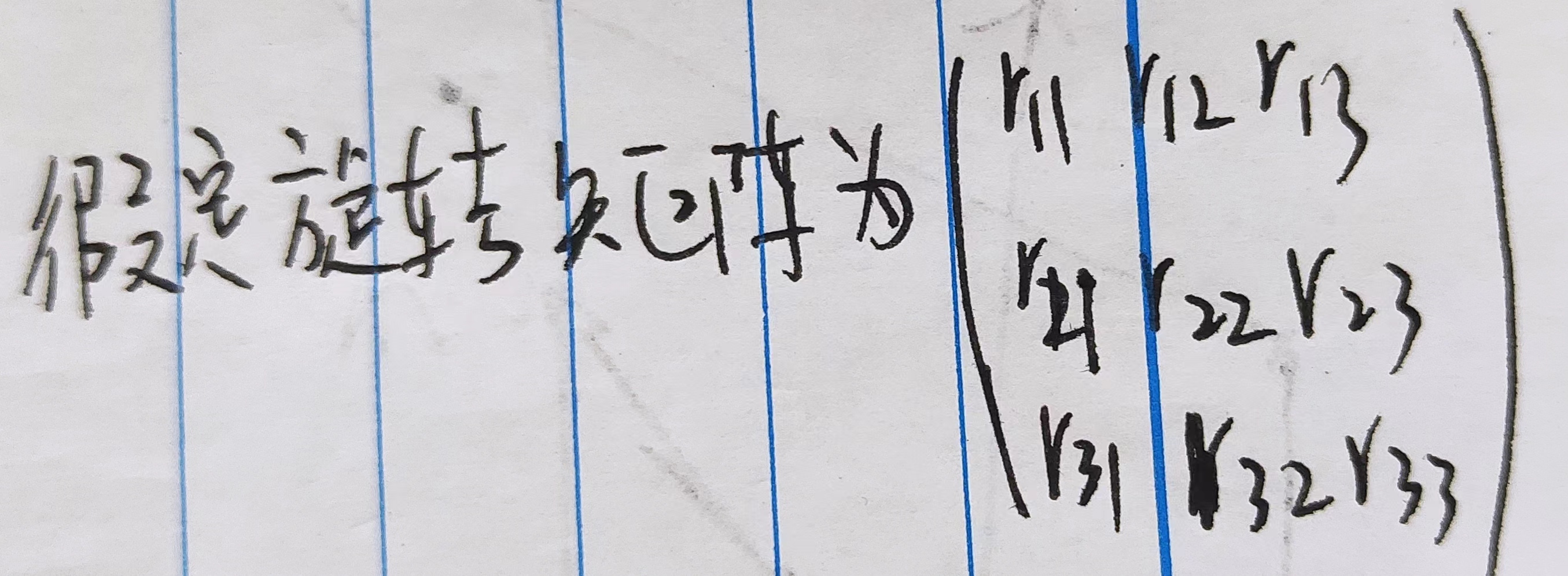
那么投影矩阵可以写成
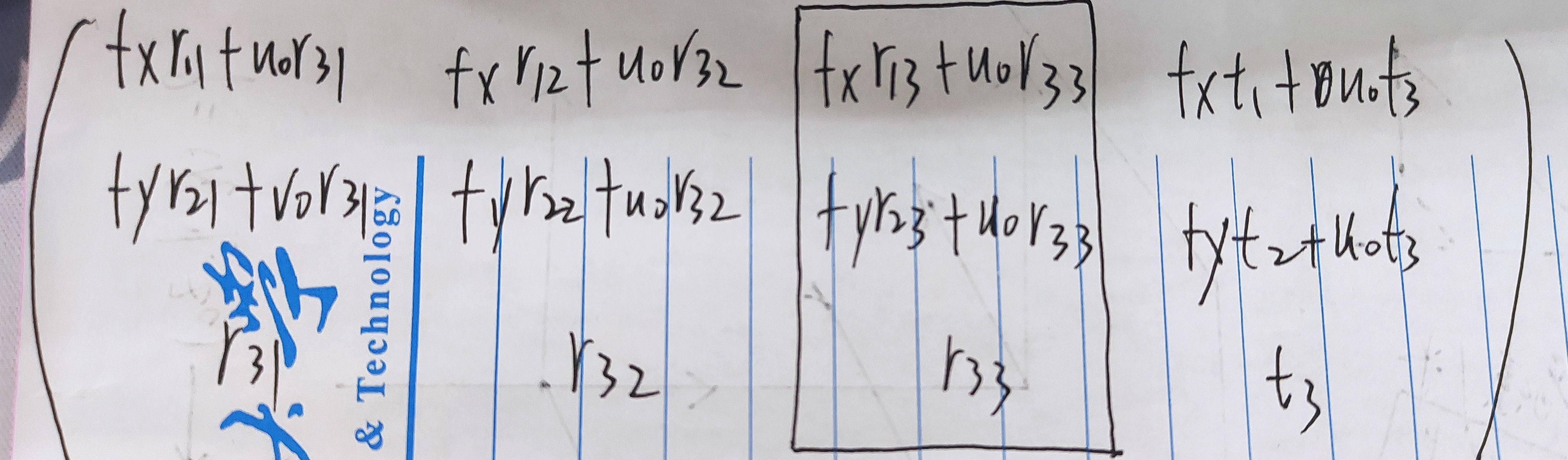
将投影矩阵简化和世界坐标相乘,并且令Zw为0,可以看到投影矩阵矩阵的第三列因为0而全被消除了,也就是旋转矩阵的第三列全部被消除了。
————————————————————————————————————————————————————
备注:
自由度问题:
从可以下图看到单应矩阵一共有9个自由度:内参5个外参旋转矩阵(x,y)平移矩阵(x,y)4个,因为Zw=0,旋转矩阵和平移矩阵就只有2维了

———————————————————————————————————————————————————

上式中的XY和uv均为棋盘格的角点,uv是通过角点检测得到的,而XY是可以观测到的和上面一样例如棋盘格的尺寸为5毫米,则左下角角点的右边那个角点坐标X就是5,Y就是0。
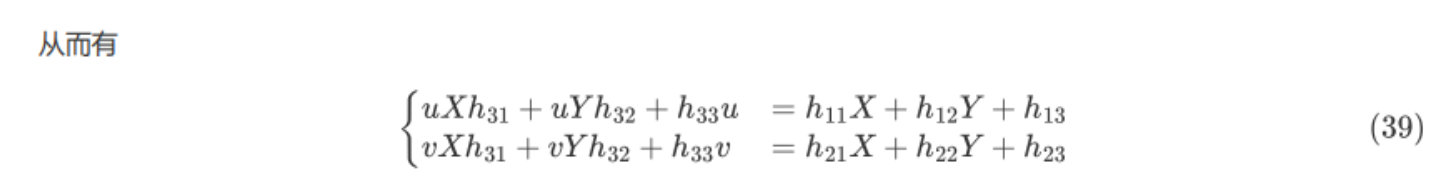

想要求一个3*3的单应矩阵仅靠一对点两个方程是不够的,先判断一下单应矩阵有9个未知量但是实际上想要根据最小二乘法求解的话就要求所有未知数平方相加的模为1
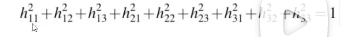
再根据所有未知数平方相加的模为1,因此这个地方就8个自由度了,因此至少需要4对点,当然由于噪声的影响,需要的方程远远多于未知数的个数,是一个超定方程,该方程如下:

最后利用最小二乘法求解上式
值得注意的是一张棋盘格对应一个单应矩阵。
内外参的求解
由于最小二乘解使单应矩阵中各个元素平方加和为1,因此求出的单应矩阵需要在前面乘以一个λ才等于实际的单应矩阵




实际上因为噪声的影响,我们会使用多张图片求解上式,得出B矩阵一般是12~14张,得到B矩阵后我们可以根据![]()
利用cholesky分解就可以求出A然后就可以求出其内部的所有参数,结果如下:
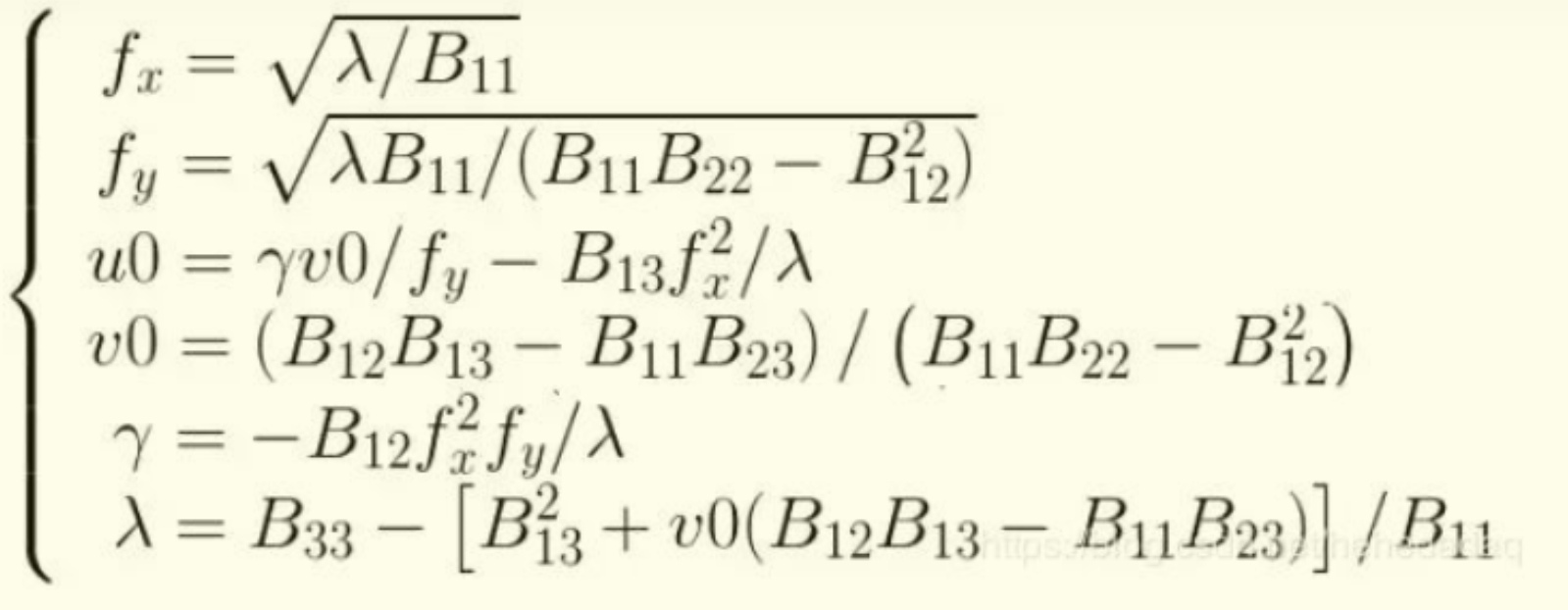
此时求出的内参矩阵依然因为最小二乘法要求B112+B122+B222+B132+B232+B332=1而和真实的内参矩阵相差一个系数,之后可以利用非线性优化的方法使内参矩阵的结果更加精确。
—————————————————————————————————————————————
备注:不能这样求内参,因为ra~b少一维,不再满足正交性

____________________________________________________________________________________________


上述表达式的意思是,我们求得的旋转矩阵是Q,我想找到一个正交矩阵R,它和Q的差值最小,最接近

棋盘格的拍摄方法
基本的相机标定方法:
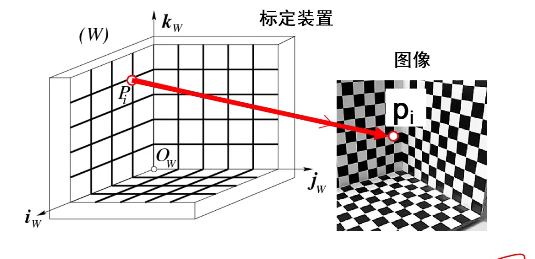
拍摄一张标定装置的图片,取这张图片上的多个点(注意每个平面上只能最多取三个点,因为三个点确定一个平面,当有第四个点时,第四个点可以由三个点来表示,最终求得的结果也是错误的)的像素坐标和世界坐标,从而计算出内外参。当然为了计算准确可以拍多张图片,将所有的内参取平均,外参描述的是相机的位姿因此不用选。
张正友相机标定法:

一般是将棋盘格打印出来贴在一个平整的板子上,固定相机调整棋盘格的位置,拍摄多组棋盘格图像,或则固定棋盘格,从不同角度拍摄棋盘格图像,首先根据每张棋盘格图像上的所有角点求出单应矩阵,然后根据所有棋盘格图片求出一组内外参数,一般要拍摄12张





