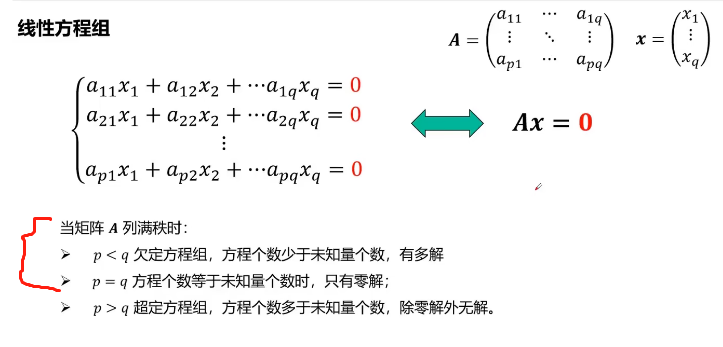
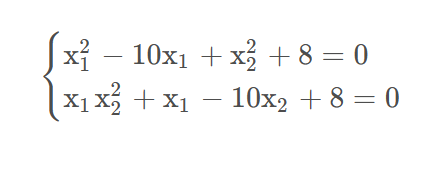线性
齐次线性方程组的解空间:
齐次线性方程组一定有一个零解,因此它分只有零解和有非零解的两种情况

按超定方程去理解解的问题:
非齐次线性方程组的解空间:

按超定方程去理解解的问题:

齐次线性方程组只有零解想求非零解时,非齐次线性方程无解想求解时,可以用最小二乘法来求解近似解。
下面阐明最小二乘问题:
1.非齐次方程的最小二乘解:

举个例子:

为什么一定要求平方项呢,原因是当我们利用最小二乘求解非齐次线性方程的解时,由于我们实际上是求不出解的,那么我们就应该得到一个最优解,这个最优解使得Ax和b最为接近,如果我们构建F(x)=|Ax-b|(绝对值才能体现出接近程度),然后求它的最小值也就是使F(x)最小,显然是不现实的,因为求导过后x就没了,因此我们可以构建平方项,使得平方项最小,此时|Ax-b|也一定是最小的。
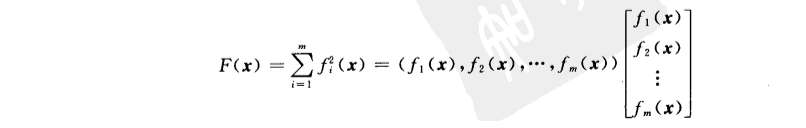


一张总结的图片:

求解方法1就是上面所述,其中求解方法2解决求解方法1括号中不可逆或则括号中计算过程过于麻烦的问题
注意最小二乘解既是非齐次线性方程的近似解同时也是使E(x)达到最小的解
2.齐次线性方程的最小二乘解:

因此我们必须将解x进行约束使它的模为1
注意最小二乘解既是齐次线性方程的近似解同时也是使E(x)达到最小的解

证明:方法一




证明:方法二
根据奇异值分解的求解过程可知

因此由上述可知方法一和方法二是一样的
非线性
![]()