几种畸变类型:
1.径向畸变:(沿着成像半径方向造成的偏差)
其畸变模型为:
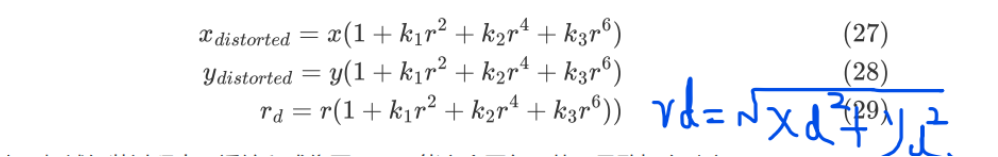
其中K1用来校正变化小的中心位置,K2用来校正变化大的边缘位置,K3用来校正鱼眼镜头,一般的镜头只需要用到K1K2,过于详细的模型(也就是取k4及以上)会导致数值的不稳定(cause numerical instability)
由畸变模型我们可以看到:
(1)
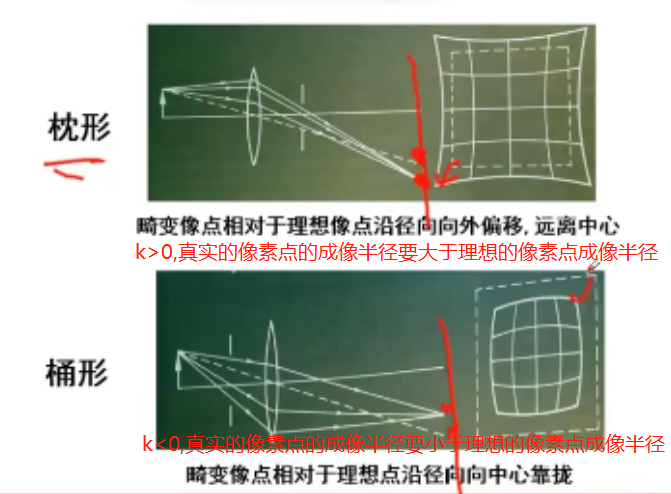
注意上图中的中心指的是光心。
(2)径向畸变只和成像半径有关:
正径向畸变(枕型畸变)k是大于0的,表明离主点距离越远畸变越大,负径向畸变(桶型畸变)表明离主点距离越近畸变越大。

上图为枕型畸变
(3)总的来说:径向畸变因为透镜的薄厚不一,折射率不同,最终使图中的直线变成曲线。
2.切向畸变
其畸变模型为:

切向畸变的产生原因是在机械组装过程中,透镜和成像平面不可能完全平行,切向畸变光的折射角越大畸变越大。

相机畸变模型的建立:
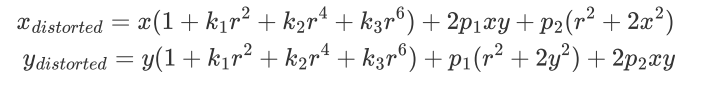
从而有:

由于畸变主要是径向畸变因此不考虑切向畸变,畸变系数一般仅考虑K1K2因此将上式进行展开(v也同理):

上述可得到:
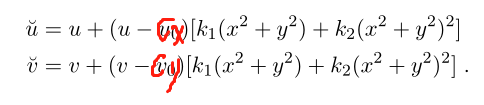
写成矩阵的形式:
![]()
值得注意的一点是,张正友标定法并没有求取焦距f的方法,因此理想的图像坐标x,y无法求得:
______________________________________________________________________________________
备注:
 ______________________________________________________________________________________
______________________________________________________________________________________
我们可以使用相机坐标代替图像坐标构成一个新的非线性方程
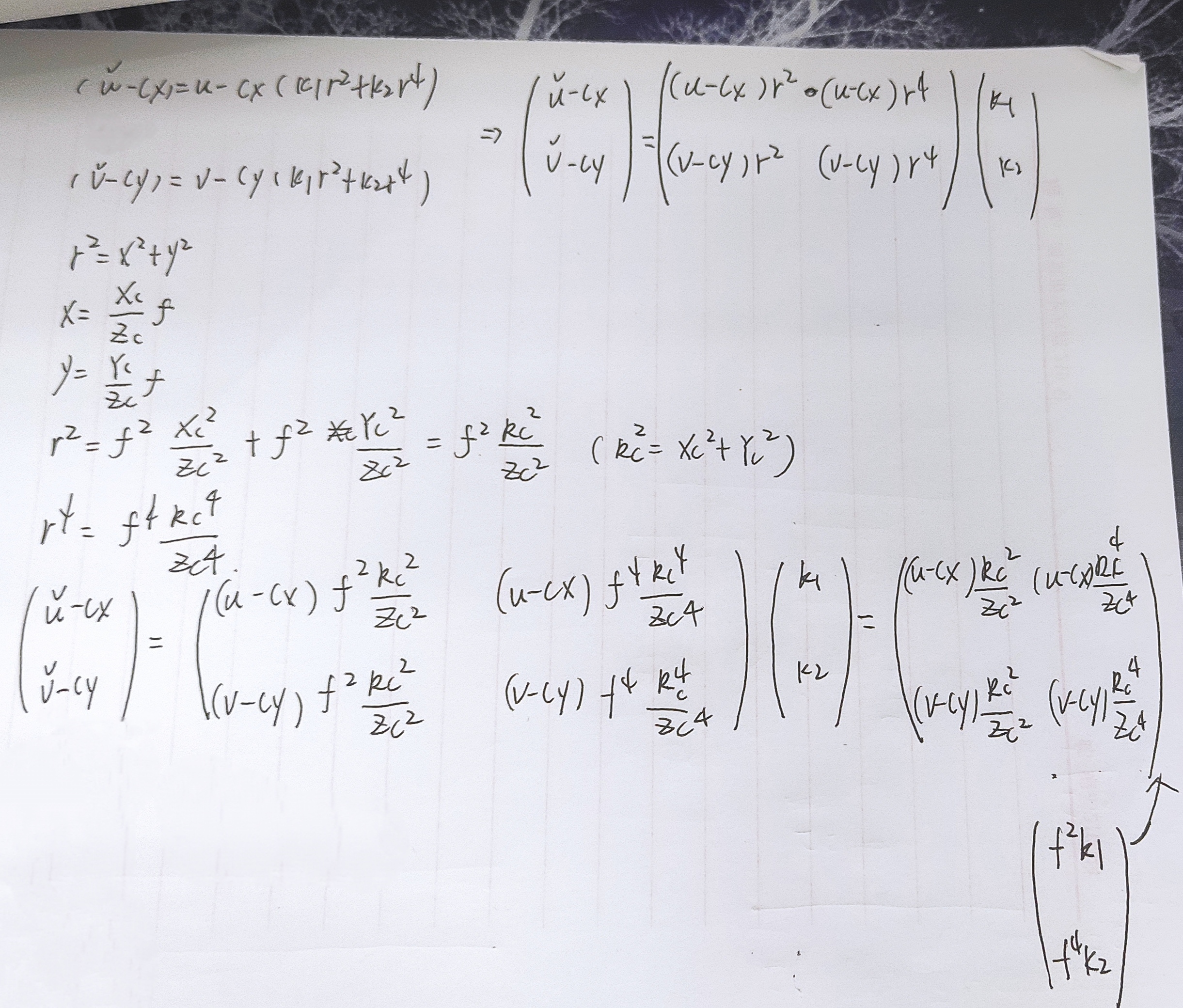
令f2k1=k'1,f4k2=k'2
畸变系数k'1k'2的求解:

以上引用张正友的论文大概意思是:由于径向畸变同样的很小,将相机标定得到的内外参数作为初值忽略畸变参数K1K2进行非线性优化(优化模型是重投影误差),具体做法如下:

之后根据优化后得到的内外参数和对应像素的世界坐标得到理想的像素坐标u,v,这样再根据角点检测(再经过亚像素处理)得到的有畸变的像素坐标![]()
![]() ,再根据上述畸变模型求得K'1K'2。
,再根据上述畸变模型求得K'1K'2。
根据畸变模型可知,我们有一对点就可以求出K'1K'2了,但我需要使用最小二乘法进行优化。
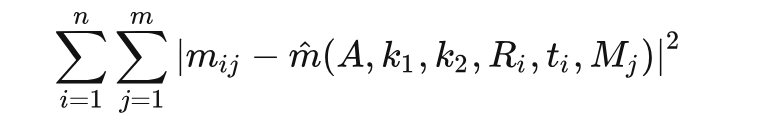
上述内外参数初值是通过非线性优化得到的。
至此求得了内外参数和畸变参数。
畸变矫正
我们知道了左右图像的分辨率就知道了理想的图像中有哪些像素坐标,比如第一个像素的像素坐标为(0,0),但是由于畸变的影响这个像素偏离了原来的位置,我们可以根据畸变模型求出这个像素在畸变后的图像的位置,然后将这个位置的像素值赋给(0,0)像素。但是我们根据畸变模型求出的坐标往往不是一个整数,因此我们需要在畸变图像上进行双线性插值求出整数的坐标



