先来看下针孔相机的成像模型:
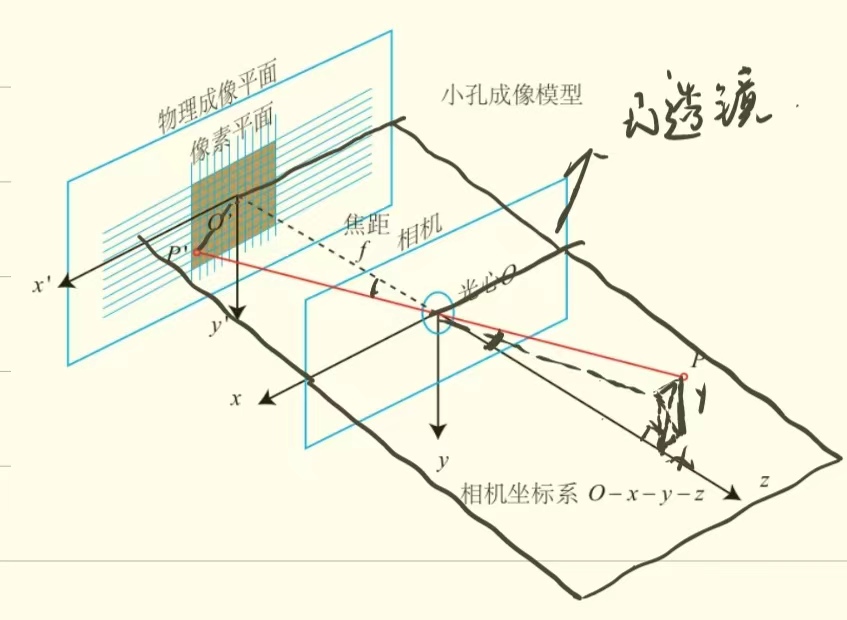
为了数学建模的方便，通常将成像平面放到凸透镜和物体之间，此时和以上两种成像模型不同的是以上两种是倒立的像，而该成像模型是正像
齐次坐标：
齐次坐标（homogeneous coordinates）是射影几何常用的一种表示形式，简单来说其采用增加 一个维度的方式来描述当前点，如常见的2D/3D 点最后维度补1，实际使用时保证该值为1（比如 除以该值）。其可以非常方便的描述射影几何的一些特殊情况，如无穷远点（最后一位补0）等。这里我们使用该方式以方便后续的矩阵运算，如从相机坐标变换至世界坐标等。
如前所述，为了将齐次坐标（x，y，w）转换为笛卡尔坐标，我们只需将x和y除以w即可。
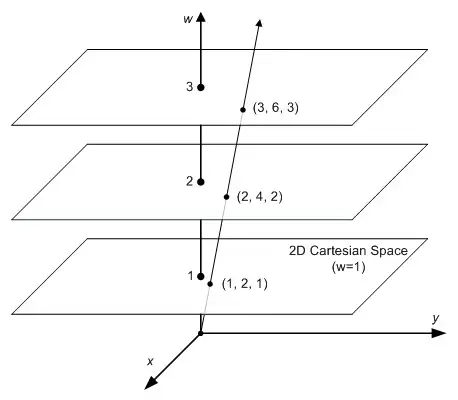
将Homogeneous转换为Cartesian，我们可以发现一个重要的事实。让我们看看下面的例子。
如你所见 (1, 2, 3), (2, 4, 6)和(4, 8, 12)这三个点对应于同一个欧氏点(1/3, 2/3). 而任何乘以a的数（1a，2a，3a）与欧氏空间中的（1/3，2/3）是同一个点。因此，这些点是 “homogeneous/齐次 “的，因为它们在欧氏空间（或笛卡尔空间）中代表同一个点。换句话说，齐次坐标是与乘数a不相关的。齐次坐标中从原点出发的射线上的所有点映射到欧式空间中属于同一点。
几个坐标系:
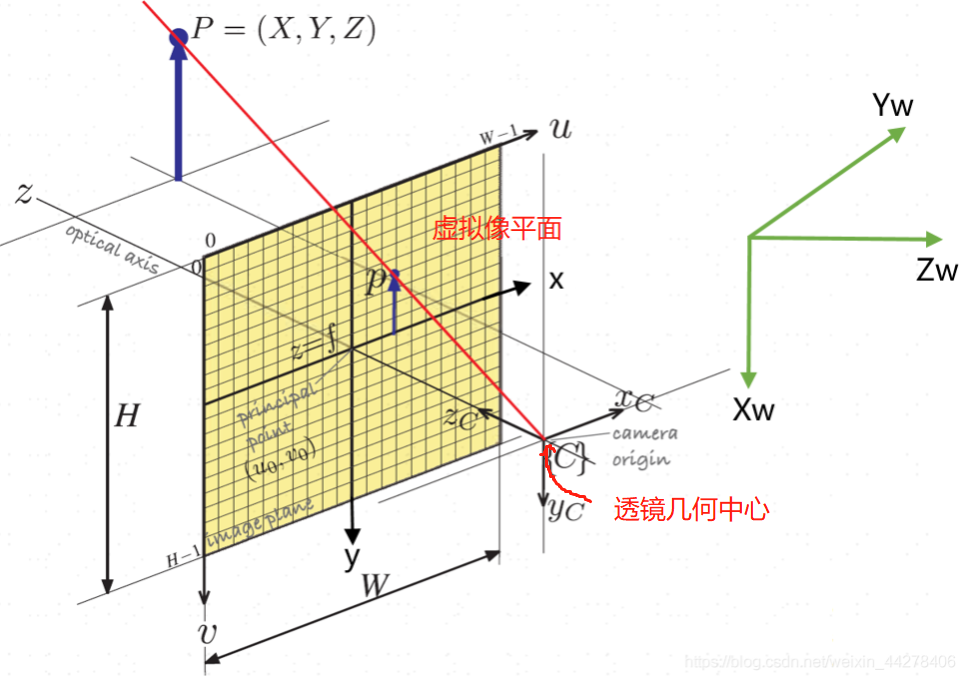
1.像素坐标系：原点位于图像左上角，(u,v),u方向朝右，v方向朝下
像素坐标系的坐标表示物点映射到图像平面的像点在像素坐标系下的位置
2.图像坐标系：原点位于相机光心与成像平面的交点，这个交点也称为主点，通常情况下是像平面的中心，(x,y),x方向朝右，y方向朝下
图像坐标系的坐标表示物点映射到图像图像平面的像点在图像坐标系下的位置
图像坐标系和像素坐标系转换：
（所做的事：物体上某一点，根据其在图像坐标系下的坐标和图像坐标系与像素坐标系的关系，求取它在像素坐标系下的坐标）
注意这里面dx,dy的单位是毫米/像素，表示每个像素多少毫米，这两个量有的时候值不同。
3.相机坐标系：原点位于相机的光心，与图像坐标系平行且方向一致，z轴可以通过右手坐标系的规则确定，相机的光心可理解为相机透镜的几何中心
物点相机坐标系下的坐标表示物点在相机坐标系下的位置
相机坐标系和图像坐标系相互转换：
（所做的事：将三维坐标转换成二维坐标，损失了距离信息，并且三维坐标系下的XC,YC和二维坐标系下的x,y不是完全重合，可以通过相似三角形已知相加坐标系下的XCYC坐标求得图像坐标系下的x,y坐标）
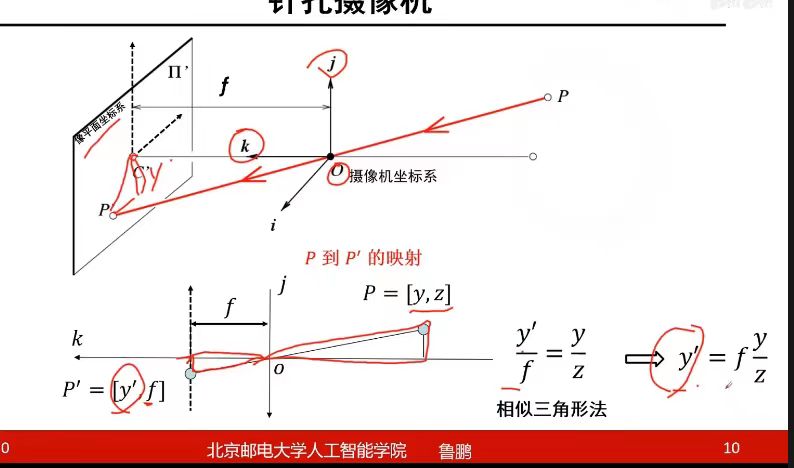
- XC，YC和x,y互相平行，方向可以不相同，这里摄像机坐标系的XC和图像坐标系的x相反的原因是相机成的像是倒立的像，但用于数学研究的虚拟像平面的x和XC方向相同。
- 想利用相似三角形求比如y的值，可以使XC，x为0，这样就可以在jok平面和yok平面，(其实两者是处于同一个平面上)构建相似三角形，以此来求得y
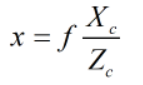
这样中间的3*4为矩阵相对于每个相机本身来说是不变的，我们就得到了线性的关系
有个问题值得注意，由于制造工艺的问题，像素可能不是正方形的，像素的x方向和y方向有一定的夹角，因此我们引入一个参数γ，它和夹角的cot值有关，当角度为90度时，它的值为0因此内参矩阵可以写成：
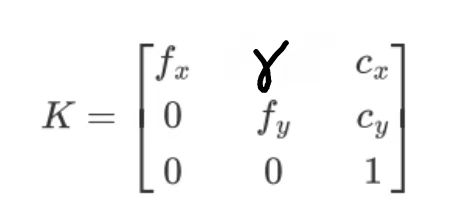
这里面注意下自由度的概念：有几个互相独立的未知数就有几个自由度，内参矩阵中所有参数显然不能用其他参数表示，因此有5个自由度
4.世界坐标系：
世界坐标系是实际物体所在的坐标系，为简便计算将图像的左下角作为世界坐标系的原点。
物点世界坐标系下的坐标表示物点在世界坐标系下的位置
世界坐标转换成相机坐标系需要刚体变换（旋转和平移）：
（所做的事:物体上的某一点，根据其在世界坐标系下的坐标和世界坐标与相机坐标的关系求取它在相机坐标系下的坐标）
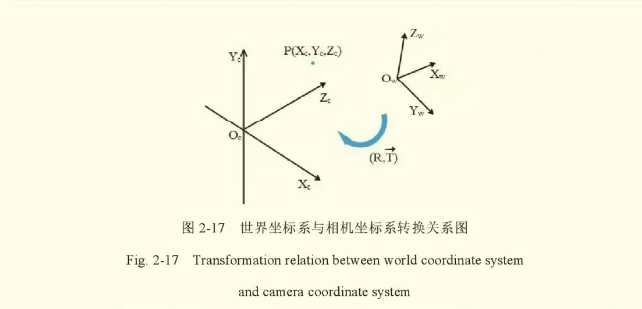
（1）旋转矩阵的性质（旋转矩阵就是正交矩阵）：
旋转矩阵是行列式为1的正交矩阵(正交矩阵的行列式为±1)，这表明旋转矩阵的列向量或则行向量为单位向量，模为1。
5.世界坐标转换成像素坐标：
针孔相机加入透镜
-
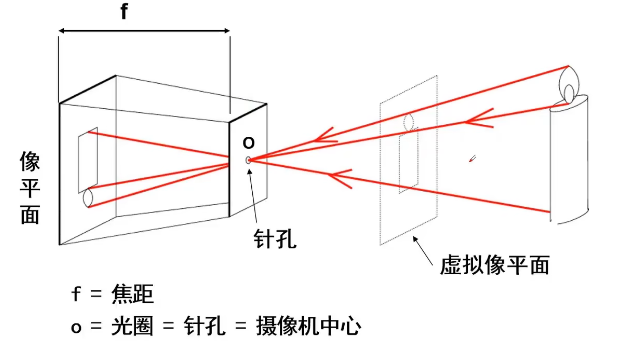
针孔相加光圈越小，图像越清晰，但是画面越暗，为了解决这个问题我们将小孔换成凸透镜，它使物体上同一点有更多的光线可以汇聚到成像平面上的同一点，这样可以增加成像的亮度和清晰度。
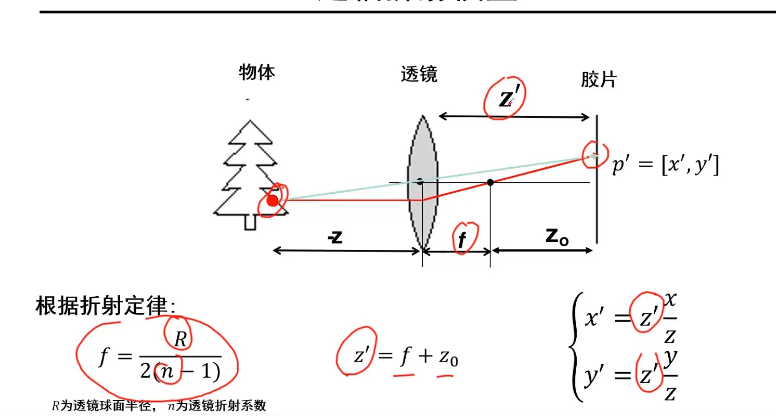
虽然加入了透镜但是它并不影响我们每一点通过光心(针孔)的光线，因此相机坐标系和图像坐标系之间的各点的关系仍然和针孔相机的相同。值得注意的是这里透镜的焦距和针孔相机的焦距是不同的。图中Z'为针孔相机的焦距，f为透镜的焦距
透镜相机可能会带来的问题：
1.失焦
景深之外的点没办法将光线汇聚在一起
2.畸变
