一.盒式滤波与积分图
盒式滤波器：
积分图的知识见积分图像 - 小凉拖 - 博客园 (cnblogs.com)
二.Hessian矩阵与DOH
每个像素的Hessian矩阵如下：
当Hessian矩阵的判别式取得局部极大值时，判定当前点是比周围邻域内其他点更亮或更暗的点，由此来定位关键点的位置，Hessian矩阵的判别式为（也就是它的行列式为Determinant of Hessian, DoH）：
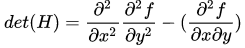
三.带有高斯核的Hessian矩阵
但是由于我们的关键点需要具备尺度无关性（唯有高斯核通过不同的方差（也就是尺度）才能体现出图像由远及近的效果，也就是所谓的尺度无关性），所以在进行Hessian矩阵构造前，需要对其进行高斯滤波。具体步骤为先对高斯核带入Hessian矩阵，然后结果矩阵的每个元素对图像进行卷积得到一个新的矩阵（此步对先对图像进行高斯卷积，再求取高斯卷积后的图像的Hessian矩阵的简便求法，这个过程用到了卷积的微分性质）。
1.卷积的微分性质：
2.复习下卷积的微积分性质：
3.高斯核带入Hessian矩阵的表达式为
分别将上述矩阵的四个元素的和图像进行卷积，以第一个元素（1，1）为例，根据高斯核进行二阶求导后生成任意尺寸的窗口，然后与图像进行卷积，该结果为
，则最终结果为H(x,y,σ)：
上述提到的简便算法为：
H(x,y,σ)的行列式为：
det(H(x,y,σ))=
四.带有盒式核的Hessian矩阵
由于高斯核是服从正态分布的，从中心点往外，系数越来越低，为了提高运算速度，Surf使用了盒式滤波器来近似替代高斯滤波器，提高运算速度。 盒式滤波器（Boxfilter）对图像的滤波转化成计算图像上不同区域间像素和的加减运算问题，只需要简单几次查找积分图就可以完成。
盒式滤波器核高斯滤波器比较
带有盒式滤波的Hessian矩阵为：
Hbox=
det(Hbox)=DxxDyy-Dxy^2
但在SURF算法中用于近似带有高斯核的Hessian矩阵的行列式的盒式矩阵的行列式得稍加修改：
权重w为了平衡因使用盒式滤波器近似所带来的误差。
这里的面积归一化处理应该就是第一节里面的盒式滤波的归一化，这里的滤波响应是Hessian矩阵的行列式。
这最终用于SURF的响应为
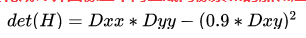
使用近似的Hessian矩阵行列式来表示一个图像中某一点处的斑点响应值（斑点通常是指与周围有着颜色和灰度差别的区域），遍历图像中的所有像素，便形成了在某一尺度下斑点检测的响应图像。使用不同的模糊尺度和模板尺寸，便形成了多尺度斑点响应的金字塔图像，利用这一金字塔图像，可以进行斑点响应极值点的搜索定位，其过程与SIFT算法类似。总结起来就是求盒式滤波的Hassian矩阵，然后将Hassian矩阵的各个元素与原图像卷积，之后求Hassian矩阵的行列式作为最终的像素值
五.SURF变换的步骤
1.构建尺度空间
要想检测不同尺度的极值点，必须建立图像的尺度空间金字塔。一般的方法是通过采用不同σ的高斯函数，对图像进行平滑滤波，然后重采样获得更高一层的金字塔图像。SIFT算法中是通过相邻两层高斯金字塔图像相减得到DoG图像，然后在DoG金字塔图像上进行关键点检测。与SIFT特征不同的是，SURF算法不需要通过降采样的方式得到不同尺寸大小的图像建立金字塔，而是借助于盒式滤波和积分图像，不断增大盒式滤波模板（上采样），通过积分图快速计算盒式滤波的响应图像。然后在响应图像上采用非极大值抑制，检测不同尺度的关键点。SURF算法的近似DoH金字塔如下图所示：
我们使用9×9的模板对图像进行滤波，其结果作为最初始的尺度空间层（此时，尺度值为s=1.2，近似σ=1.2的高斯微分），至于为什么是1.2为什么是9×9这个论文原文没有说，记住就行了。这样盒式滤波组成的金字塔，每层的尺寸是完全固定的，不随图像的改变而改变。那么盒式滤波的最初尺度空间层的Dxx,Dyy，Dxy也是固定的，其模板如下
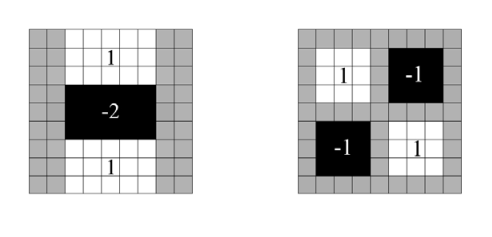
上图分别给出了Dyy,Dxy，它们近似的1.2尺度的高斯二阶微分如下：
接下来增大盒式滤波器的模板
21怎么求出来的呢：(5+2)×3, 27怎么求出来的呢(7+2)×3,以此类推。
9×9到27×27作为第一组的所有模板
第二组的初始模板为9+6×2^m-1(m=1,2,3……),m是组数减1，那么第二组的模板为(15，27，39，51)，第三组为(27，51，75，99)
注意增大模板增大的是Dxx,Dxy,Dyy的模板，三个模板都遵循以上规则。
构建好模板接下来就是将Hassian矩阵的各个元素Dxx,Dxy,Dyy与原图像卷积，之后求Hassian矩阵的行列式作为最终的像素值，至此构建好了SURF的金字塔。
2.关键点的定位
和SIFT算法一样，这里和DoG不同的是不用剔除边缘导致的极值点了，因为Hessian矩阵的行列式就已经考虑到边缘的问题了。
注意这里的σ求法为：
3.主方向的确定
个人认为在求完每层的极大值后，这些极大值是亚像素点，哪一层的σ为与亚像素点的σ最接近就选哪一层。接下来在被选为确定主方向的层中的关键点的位置以6*s（s=1.2∗L/9为关键点的尺度）为半径的圆形区域，对图像进行Haar小波响应运算（就是以Haar小波的模板对该区域中的图像进行滤波，该模板的尺度为4s×4s,该模板的中心对准所求像素点）。
其中左侧模板计算X方向的响应，右侧模板计算y方向的响应，黑色表示-1，白色表示+1。用其对圆形领域进行处理后，就得到了该领域内每个点对应的x,y方向的响应，这里分别得到了一个x方向的响应和y方向的响应图像，然后用以关键点为中心的高斯函数（）对这些这两幅图像的响应进行加权（每一个图像乘以他的权值）。
为了求取主方向值，需要设计一个以关键点为中心，张角为60度的扇形滑动窗口，统计这个扇形区域内的haar小波特征总和。以步长为0.2弧度左右，旋转这个滑动窗口，再统计小波特征总和。小波特征总和最大的方向为主方向。特征总和的求法是对图像Harr小波响应值dx、dy进行累加，得到一个矢量：
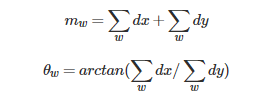
主方向为最大Harr响应累加值所对应的方向，也就是最长矢量所对应的方向，即
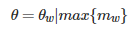(也就是最大mw对应的θw）
可以依照SIFT求方向时策略，当存在另一个相当于主峰值80%能量的峰值时，则将这个方向认为是该特征点的辅方向。一个特征点可能会被指定具有多个方向（一个主方向，一个以上辅方向），这可以增强匹配的鲁棒性。和SIFT的描述子类似，如果在中出现另一个大于主峰能量
的80%时的次峰，可以将该特征点复制成两个特征点。一个主的方向为最大响应能量所对应的方向，另一个主方向为次大响应能量所对应的方向。
4.特征描述子的求取
以关键点为中心选取一个正方形框住一个图像区域，再将此区域中所有像素点连同这个区域旋转到关键点的主方向（关键点到矩形边框的线段表示关键点的主方向），边长为20S。将其划分为16个区域（边长为5S，也就是被划分为4×4个子块），每个子块利用尺寸2s的Harr模板对该5S×5S子块内所有像素响应值计算，然后对所有像素的响应值进行统计∑dx、∑|dx|、∑dy、∑|dy|（所有像素x方向响应的加和，所有像素x方向响应绝对值的加和，所有像素y方向响应的加和，所有像素y方向响应绝对值的加和，且注意dy沿主方向，dx垂直于主方向）形成特征矢量。
特征描述子共由4×4×4=64维特征矢量组成。
SURF描述子不仅具有尺度和旋转不变性，还具有光照不变性，这由小波响应本身决定，而对比度不变性则是通过将特征向量归一化来实现。
一般而言，特征矢量的长度越长，特征矢量所承载的信息量就越大，特征描述子的独特性就越好，但匹配时所付出的时间代价就越大。对于SURF描述子，可以将它扩展到用128维矢量来表示。具体方法是在求∑dx、∑|dx|时区分dy<0和dy≥0情况。同时，在求取∑dy、∑|dy|时区分dx<0和dx≥0情况。这样，每个子块就产生了8个梯度统计值，从而使描述子特征矢量的长度增加到8×4×4=128维。
为了实现快速匹配，SURF在特征矢量中增加了一个新的变量，即特征点的拉普拉斯响应正负号。在特征点检测时，将Hessian矩阵的迹的正负号记录下来，作为特征矢量中的一个变量（Hessian矩阵的迹为拉普拉斯响应）。这样做并不增加运算量，因为特征点检测进已经对Hessian矩阵的迹进行了计算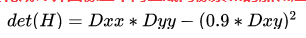（）。在特征匹配时，这个变量可以有效地节省搜索的时间，因为只有两个具有相同正负号的特征点才有可能匹配，对于正负号不同的特征点就不进行相似性计算。
简单地说，我们可以根据特征点的响应值符号，将特征点分成两组，一组是具有拉普拉斯正响应的特征点，一组是具有拉普拉斯负响应的特征点，匹配时，只有符号相同组中的特征点才能进行相互匹配。显然，这样可以节省特征点匹配的时间。
实际上有文献指出，SURF比SIFT工作更出色。他们认为主要是因为SURF在求取描述子特征矢量时，是对一个子块的梯度信息进行求和，而SIFT则是依靠单个像素梯度的方向。
以上只是个人理解，欢迎批评指正。
参考文章：
(53条消息) 【OpenCV 例程200篇】56. 低通盒式滤波器_YouCans的博客-CSDN博客_盒式滤波
