一、向量的内积和几何意义（点乘）
对于向量a和向量b：
1、a和b的内积公式为：
要求一维向量a和向量b的行列数相同。
2、内积的几何意义
a·b=||a|| ||b||cosW
点乘的几何意义是可以用来表征或计算两个向量之间的夹角（大于0夹角小于90，等于0向量之间垂直，小于0向量之间大于90），以及在b向量在a向量方向上的投影。（表示b在a上的投影（或是a在b上的投影）||b||cosβ，长度是||a||）
二、向量的外积和几何意义（叉乘）
A×B=|A||B|sinW
两个向量的外积，又叫向量积、叉乘等。外积的运算结果是一个向量而不是一个标量。并且两个向量的叉积与这两个向量组成的坐标平面垂直。
对于向量a和向量b：
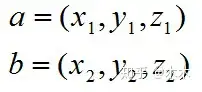
1、a和b的外积公式为：
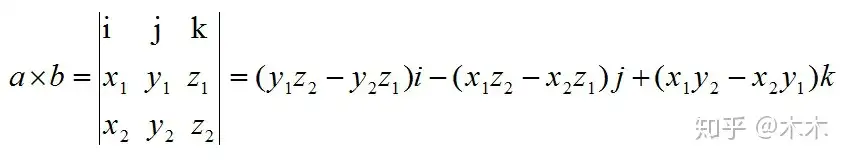
其中：
根据i、j、k间关系，有：
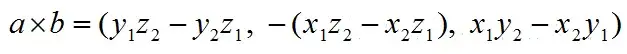
2、叉乘几何意义
在三维几何中，向量a和向量b的叉乘结果是一个向量，更为熟知的叫法是法向量，该向量垂直于a和b向量构成的平面。
