第46件事 运营策略优化

很多人说产品经理的职业规划差不多是这样的：5年专业，5年管理，5年经营，不管是做管理还是经营，其核心还是归结到两个字：决策。如何做决策？如何确保做出的决策是最优或较优？尤其我们在做产品数据运营的时候，经常会碰到这样的问题。下面就谈一下其中的几个关键问题，看是如何优化决策的。

1.价格优化决策
电商、平台App Store、游戏道具等商品基本都会涉及价格，进而涉及销售量和销售额等；当然，也就离不开定价的问题。那么如何定价才能确保销售额（收入）甚至利润最大化呢？这里介绍一种常用的方法。
首先我们需要了解一下需求曲线，需求曲线表示在每一价格下所需求的商品数量。需求曲线是显示价格与需求量关系的曲线，是指其他条件相同时，在每一价格水平上买主愿意购买的商品量的曲线。一般情况是价格越高，销售量越低；价格越低，销售量越高，如图7-3所示。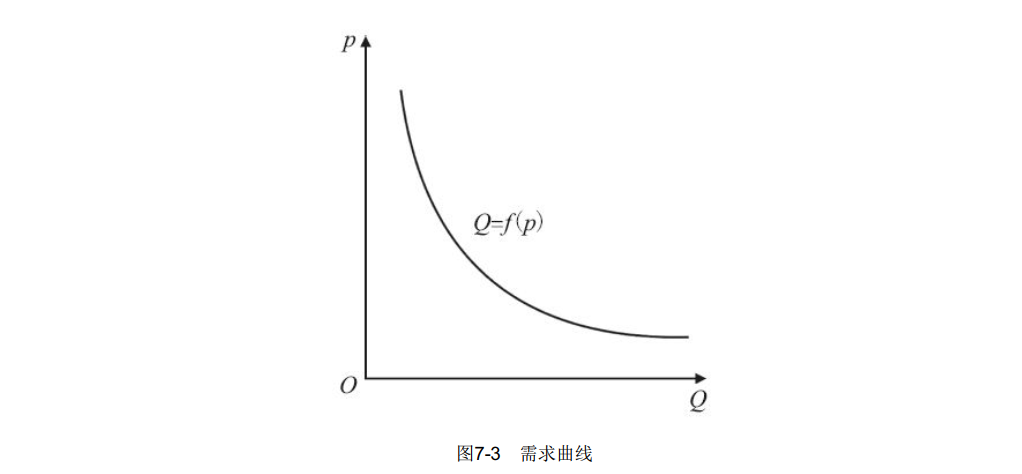

了解需求曲线之后，我们需要对需求曲线进行拟合。曲线拟合指的是通过实验获得有限对测试数据（xi，yi），利用这些数据来求取近似函数y=f（x）。式中x为输出量，y为被测物理量。与插值不同的是，曲线拟合并不要求y=f（x）的曲线通过所有离散点（xi，yi），只要求y=f（x）反映这些离散点的一般趋势，不出现局部波动。

销售量Q（销售量）是因变量，p（价格）是自变量，a、b、c是常量，需求曲线拟合后得到的销售量公式如图7-4所示。

如何求出a、b、c三个常量的值呢？这里需要用到最小二乘法。最小二乘法又称最小平方法，是一种数学优化技术。它通过最小化误差的平方和寻找数据的最佳函数匹配。利用最小二乘法可以简便地求得未知的数据，并使得这些求得的数据与实际数据之间误差的平方和为最小。对给定数据点{（Xi，Yi）}（i=0，1，…，m），在取定的函数类Φ中，求p（x）∈ Φ，使误差的平方和E2最小，E2=∑[p（Xi）-Yi]2。从几何意义上讲，就是寻求与给定点{（Xi，Yi）}（i=0，1，…，m）的距离平方和为最小的曲线y=p（x）。函数p（x）称为拟合函数或最小二乘解，求拟合函数p（x）的方法称为曲线拟合的最小二乘法。
这里需要提供3对数据，分别是（p1，Q1），（p2，Q2），（p3，Q3），一个价格对应一个销售量，使用最小二乘法求出公式中的常数a、b、c即可。求出a、b、c三个常量后，得出销售量公式，进而得出收入公式，L=p×Q=p×f（p），令收入函数L的一阶导数等于0即可得出收入最大的价格决策。
在计算出收入公式之后，进而可以得出利润公式，R=L-C=（p×Q）-（v×Q+F），C代表成本，v代表变动成本，F代表固定成本，Q代表销售量，令利润函数R的一阶导数等于0即可得出销售利润最大的价格决策。

2.广告费用优化决策
在产品运营过程中，我们或多或少会做一些或大或小的广告，一般都会添加统计代码，这样可以追踪到用户的消费行为，那么，投入多少广告费用，给我们带来的销售收入效应最大？选择哪个广告费用投放区间，我们不至于亏损？再者，投入多少广告费用，也就是每增加或减少一块钱带来的销售收入边际效应最大？这里介绍一种常用的方法。

跟价格优化决策过程类似，我们需要对广告效应曲线进行拟合，广告效应曲线函数公式中w代表费用，y代表收入，如图7-5所示。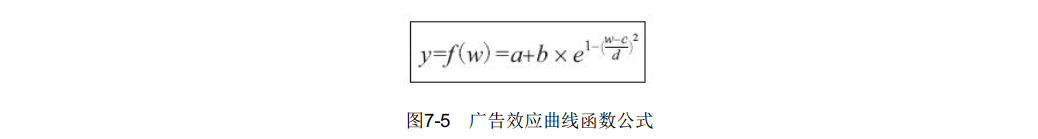

如何求出a、b、c、d这4个常量呢？同样要用到最小二乘法，这里需要提供3对数据，分别是（w1，y1），（w2，y2），（w3，y3），一个费用对应一个收入，使用最小二乘法求出公式中的常数a、b、c、d即可。

广告投入及其效应之间的关系呈现S形，如图7-6所示。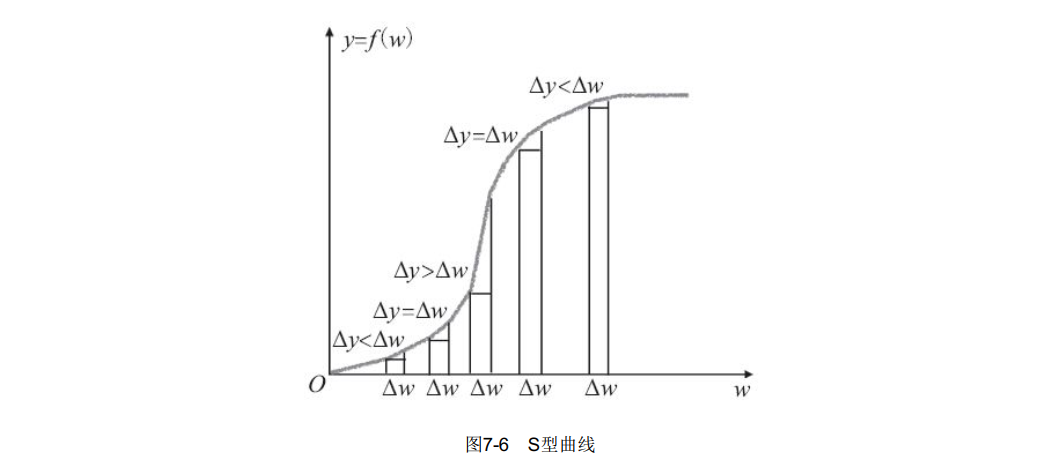

求出a、b、c、d这4个常量后，得出函数式y=f（w），令y的二阶导数等于0，即可求出收入效应最大时的广告投入费用数值。令y的一阶导数等于1，即可求出不亏损时的广告费用投入区间。

这次涉及的知识蛮多的，运筹学、财务管理、市场营销、高等数学等，还推荐了两门非常实用的课程：《现代企业决策与仿真》和《事理求精运筹学》，这两门课程在网易公开课客户端上都可以免费观看和学习。

收入或利润最大化时的价格决策一般是求取函数曲线的一阶导数等于0；收入效应最大时的广告投入费用数值（求取函数曲线的二阶导数等于0），不亏损时的广告费用投入区间（求取函数曲线的一阶导数等于1）。做出最优决策需要了解高等数学和运筹学相关的知识和技能。