AcWing 126. 最大的和

题目

算法1

前缀和，\(O(n^4)\)

#include <iostream>
using namespace std;
const int N = 110;
int s[N][N];

int main()
{
	freopen("in.txt", "r", stdin);
	freopen("out.txt", "w", stdout);
	
	int n; cin >> n;
	
	for(int i = 1; i <= n; i ++ )
		for(int j = 1; j <= n; j ++ )
		{
			cin >> s[i][j];
			s[i][j] += s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1];
		}
	
	int res = -2e9;
	for(int x1 = 1; x1 <= n; x1 ++ )
		for(int y1 = 1; y1 <= n; y1 ++ )
			for(int x2 = x1; x2 <= n; x2 ++ )
				for(int y2 = y1; y2 <= n; y2 ++ )
					res = max(res, s[x2][y2] - s[x1 - 1][y2] - s[x2][y1 - 1] + s[x1 - 1][y1 - 1]);
	cout << res;
	
	return 0;
}

算法2

线性动归，\(O(n^3)\)

这里直接引用讲义

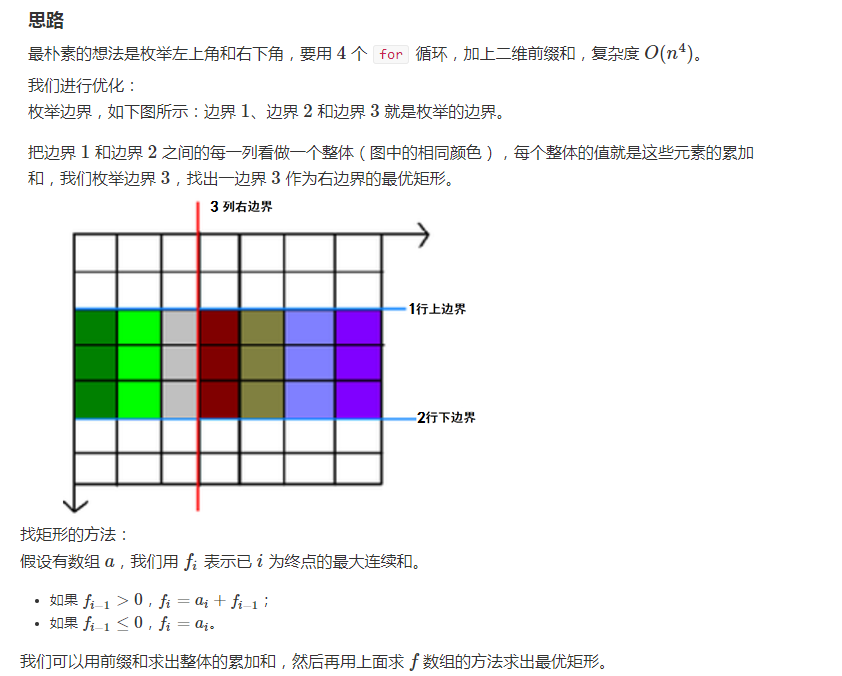
• 实际代码中，要更改前缀和的存储方式
• 因为子矩阵都是连续的，所以当上下界限确定时，当上一次计算的子矩阵大小为负时，则抛弃原矩阵；如果为0舍不舍都可以。确定了当前的状态之后，每次取最大值即可。

#include <iostream>
using namespace std;
const int N = 110;
int s[N][N];
int n;

int main()
{
	//freopen("in.txt", "r", stdin);
	//freopen("out.txt", "w", stdout);
	
	cin >> n;
	for(int i = 1; i <= n; i ++ )
		for(int j = 1; j <= n; j ++ )
		{
			cin >> s[i][j];
			s[i][j] += s[i - 1][j]; // 第j列单位为1的前i个元素的前缀和 
		}
	
	int res = -2e9;
	for(int i1 = 1; i1 <= n; i1 ++ )
		for(int i2 = i1; i2 <= n; i2 ++ )
		{
			int pre = -2e9;
			for(int k = 1; k <= n; k ++ )
			{
				pre = max(pre, 0) + s[i2][k] - s[i1 - 1][k];
				res = max(res, pre);
			}
		}
	cout << res << endl;
	return 0;
}