python基础：数据分析_Numpy

参考视频：

https://www.bilibili.com/video/BV1HJ411j7NG?p=2

首先要安装Anaconda，安装好后配置环境变量，参考：

https://blog.csdn.net/qq_40733911/article/details/87298373

安装好并配置环境变量后，打开jupyter，一旦点击运行，jupyter就会退出，显示错误：

 

最后终于发现是电脑用户名是中文的问题，然后将电脑用户名修改为英文，根据文章：

https://blog.csdn.net/qq_41137110/article/details/102644516?tdsourcetag=s_pcqq_aiomsg

修改完之后，打开系统的环境变量，将原来的中文名也修改为英文。

 

之后就可以正常使用jupyter了。

 

使用jupyter打开某路径下的文件，比如使用jupyter打开 E:\

 

 

 

▲jupyter的使用：

快捷键：

 

 

几个常用的快捷键：

shift + enter ：运行本行

点击输入框前面的部分：

a : 在本行上面增加一行

b：在本行下面增加一行

dd：删除本行（比如本行是一个变量，可以在页面上删除本行，但该变量不会删除，还是在内存中）

 

数据分析常用库：

python没有提供数组功能，而numpy的数据结构是数组。数组的运算速度比列表等数据结构运算速度快很多。

 

numpy简单介绍：

 

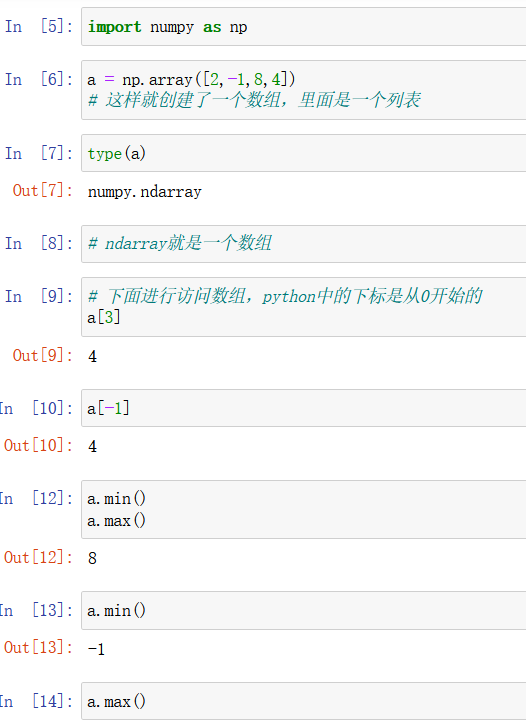
接下来创建一个二维数组：

 

注意，array中通常是一个列表。二维数组使用一个 [ ] 括起来使用的。

 

pandas简单介绍：

 

 

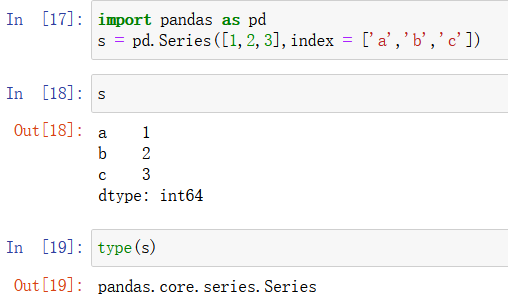
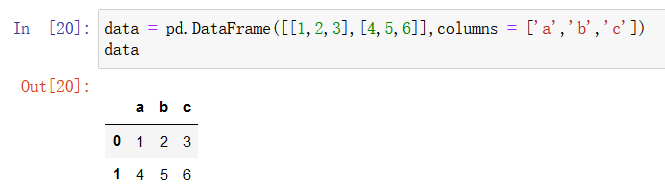
pandas 可以读取 csv、txt、excel中的数据。

如果桌面有这样一个文件：

 

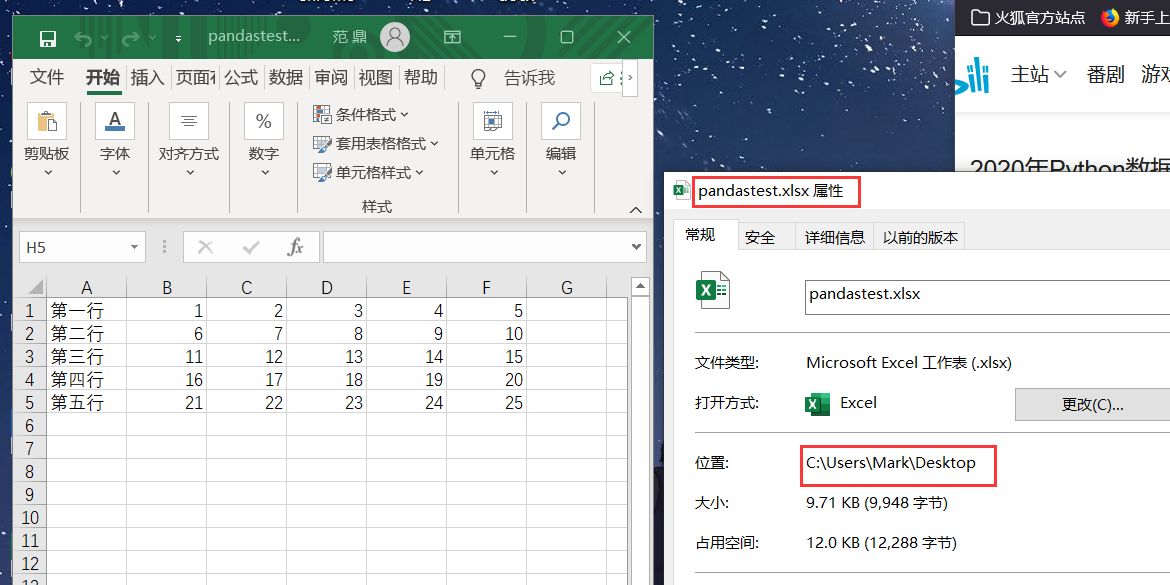
则可以这样来访问：

 

注意，需要使用两个 \\ ，第一个 \ 代表转义字符，或者直接：

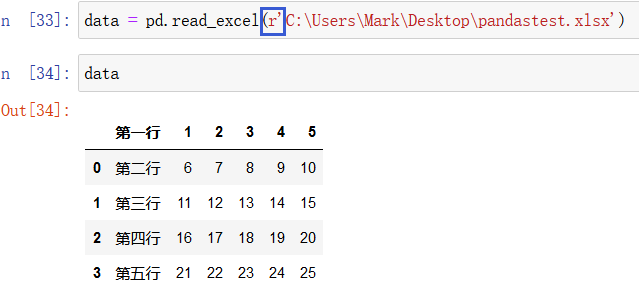
也是与加转义字符 \ 一样的效果。

 

一、Numpy基本用法

包括：数组的创建、数组的属性、索引和切片

 

▲数组创建

 

 

 

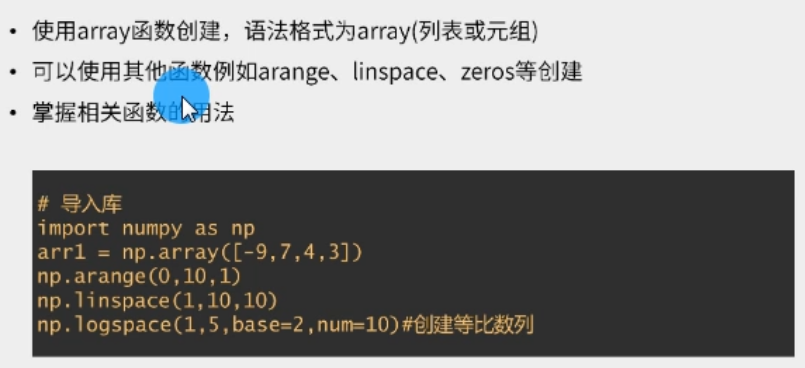
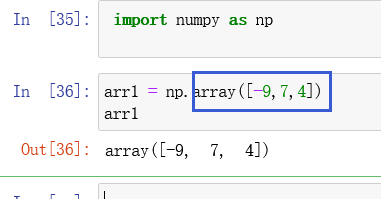
如上图所示，其中，array（）的参数是数据结构，可以是列表、元组等，一般我们写列表。

我们还可以规定数组中的数据类型：

 

创建二维数组：

 

array（）的参数是一个嵌套的列表。

 

上述创建数组的方法可能会比较麻烦，使用这一种方法来创建数组：

注意，python是左闭右开的，所以 arange(0,10) 是从0到9.

 

 

 linespace（）函数用来创建一个等差数列，上图表示创建一个从1开始到10结束，一共有5个数的等差数列。

该函数还有一个可选参数endpoint，表示是否取到最后一个数：

 

如上图所示，第一行代码要求创建从1开始到10结束，一共10个数，但是不取到最后一个数10的等差数列。如果不取到最后一个数，本质上是先创建一个 11个数的等差数列，然后去掉最后一个数。

 

创建一个全为0的数组：

 

如上图所示，zeros（）函数中若参数为[4,5],表示创建一个四行五列的，值全为0的二维数组，如果参数为 6 ，表示创建一个有6个元素的值全为0的数组。

 

创建一个单位矩阵：

 

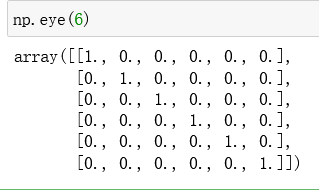
如上图所示，创建一个六阶的单位矩阵。

 

创建一个对角矩阵：

上图表示创建一个对角线为4,5,8的三阶对角矩阵。

注意，矩阵的加1是指矩阵内所有元素的值都加1，如下图所示：

 

这和列表的加1不同，列表不能直接加1，如下图所示：

 

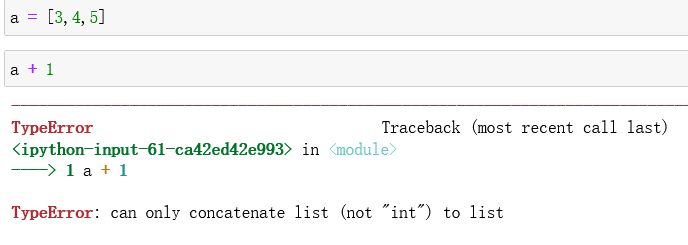
列表直接加1就会报错，列表加法只能采用迭代的方法：

 

但是如果是数组，却可以直接加1：

 

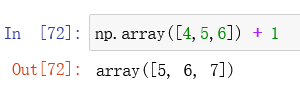
而且数组是同时运算，而列表时迭代运算，所以数组效率比列表一般要高。

 

▲数组的属性特征：

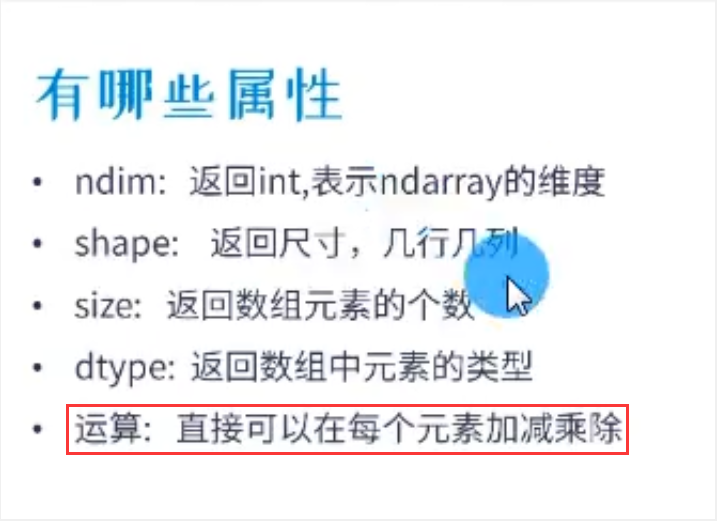
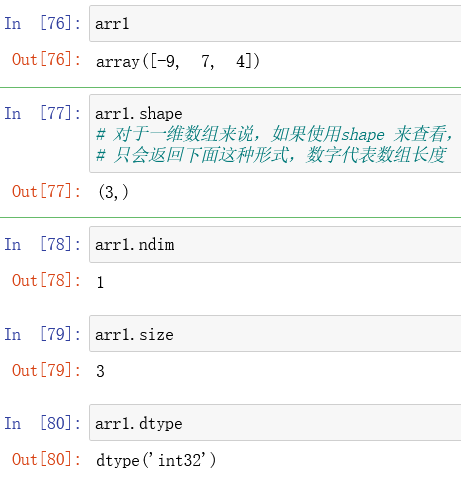
arr.shape 用来查看数组的形状（例如二维数组有几行几列）

arr.ndim 用来查看数组的维度

arr.dtype 用来查看数组中元素的类型

arr.size用来查看数组的长度

如下图所示：

 

 

 

▲索引和切片

 

普通索引：

将上图看做二维数组，上图即数组的索引，是从0开始的，有三种索引方法。

 

上图所示，python是左闭右开的，所以使用 arr[3:5] 是取不到第六位（索引从0开始）的，只能取第四、五两位。

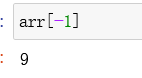
取数组的倒序：

 

取数组的最后一位：

 

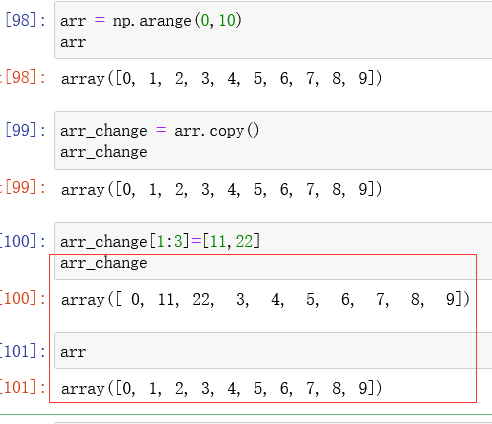
数组元素的修改：

 

如图，将数组arr赋值给arr_change，若arr_change 改变，arr也改变，这点也跟列表一样。列表解决这个的方法是使用copy（）函数（浅拷贝），数组中解决这个的方法也是使用copy（）函数。

 

 

 

二维数组：

创建一个二维数组：

 

 

如果访问时对行数不作限制，对列数做限制：

 

上图表示访问时对行数不作限制，访问第3、4两列

同样的，对列数不作限制，访问第2、3行：

 

或者可以直接：

 

 

如果要取出二维数组中所有大于3.5的元素，可以这样写：

 

取上图相反的情况：

 

其他操作：

 

 

花式索引：

访问第三行以及第二行，并且先访问输出第三行，再访问输出第二行：

输出第四行第一列，第三行第二列的元素：

 

对行不作限制，先输出第四列，再输出第二列的内容：

 

花式索引可以指定行、列的顺序，同时和普通索引区别：

 

花式索引取出的是二维的数组，而普通索引取出的可能会是一维数组：

 

分别看一下它们的维度：

 

 

还可以使用 np.ix 来返回行列数不同的二维数组：

如果要使用花式索引返回该结果，不能这样：

应该使用如下方法：

 

上图意思是先取出二维数组的第1行和最后一行；然后再对行不做限制，取出二维数组的第1、2、4列。

 

二、Numpy高级用法：

 

▲数组形状改变

 

 

 

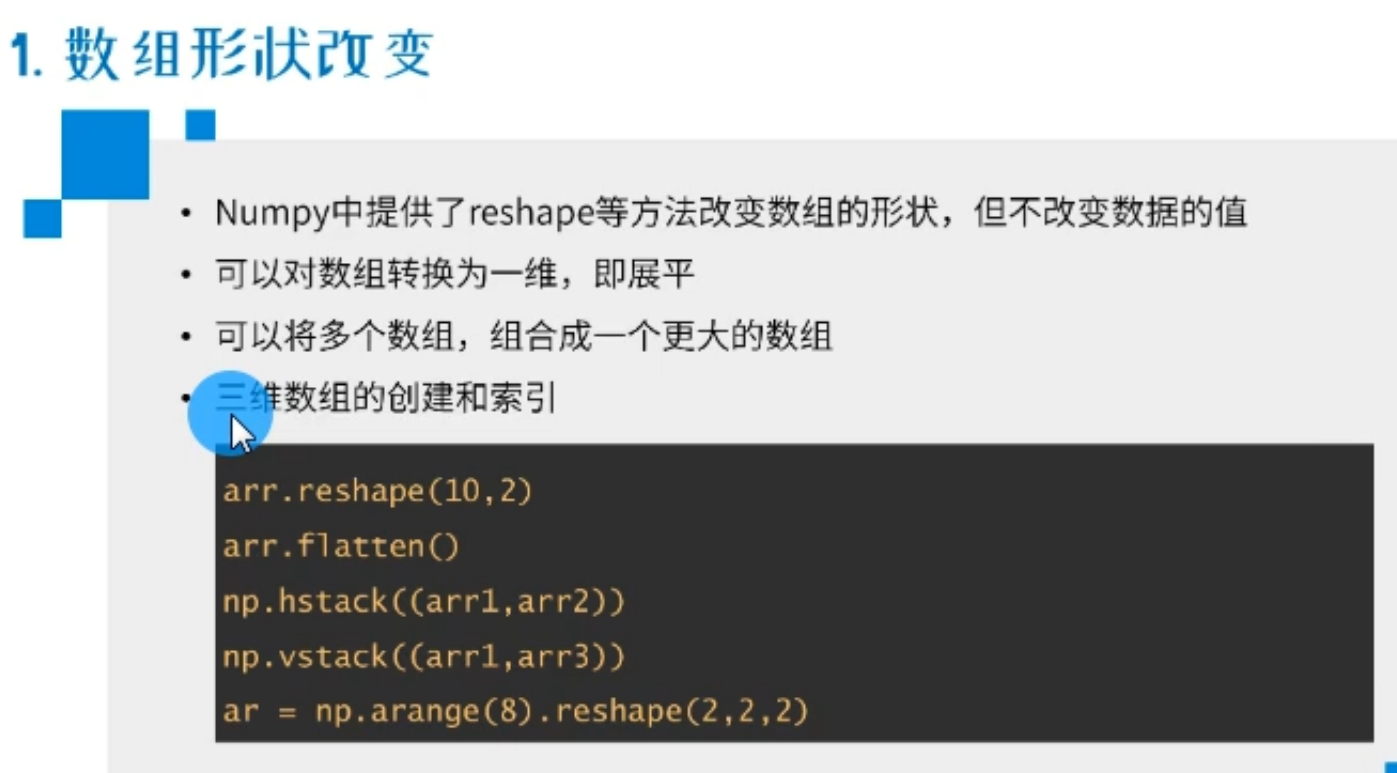
1）改变数组形状 reshape() 、resize() 、arr.shape = (x,y)

改变数组形状使用reshape（）方法，但是不会改变原数组，只会返回一个新的数组

 

 

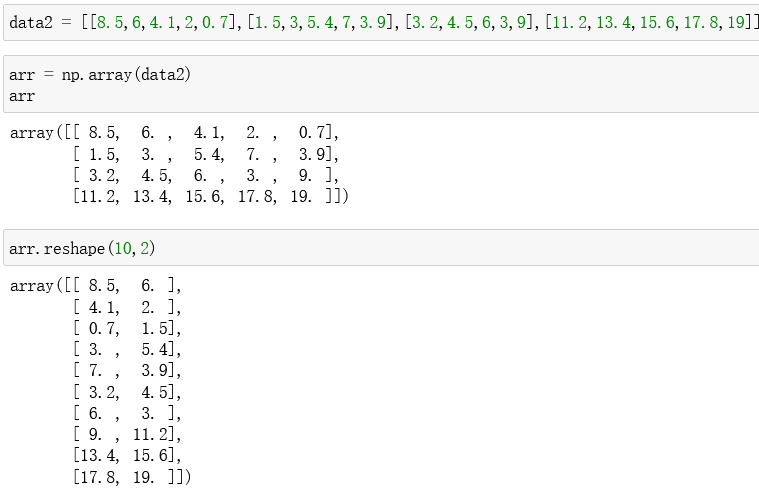
如上图所示，通过一个四行五列的二维数组返回为10行2列，原数组arr仍然是4行5列。

 

如果要直接改变原数组，可以使用 resize（）方法：

 

 

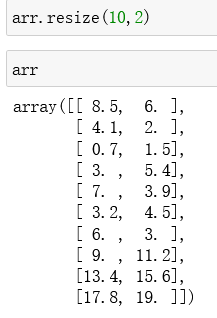
或者 使用 arr.shape = (x,y) 的方式：

 

 

 

2）数组降维

使用 ravel() 方法可以给数组降维，但是不会改变原数组，默认是按照横向来降维一维数组

 

 

 还可以加上参数 order = 'F',按照纵向将二维数组降为一维：

 

 

 

arr.flatten() 与ravel()的效果一致。

 

 

使用 reshape 方法也可以返回一个展平的数组，即返回一个降维的数组：

 

 

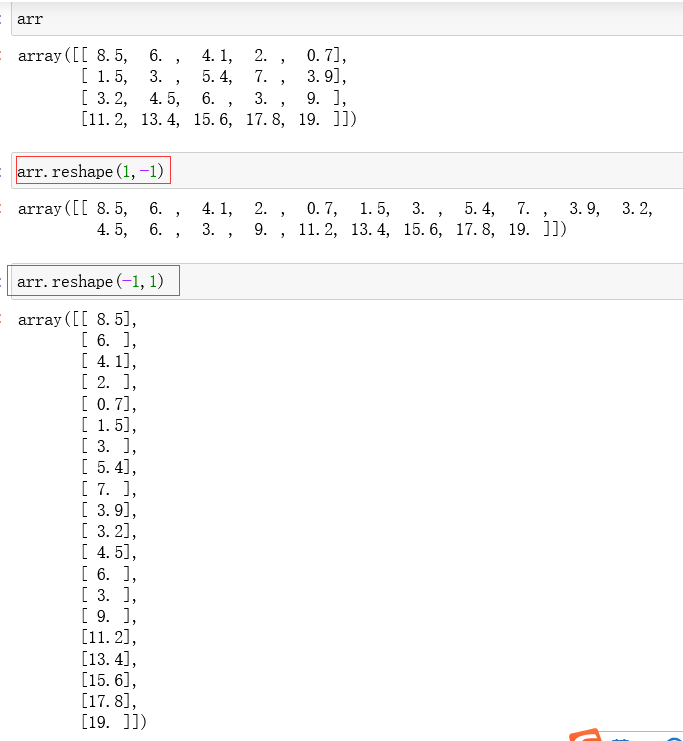
在reshape（）方法中，只要给定了一个参数，另一个参数就可以自动确定了，所以另一个参数写 -1 就可以。

如果reshape（）的参数只有一个 -1 ，那么功能就和 flatten（）和 ravel（）一致了。

flatten（）、ravel（）以及 reshape（-1）三个方法的区别为：

如果更改展平后数组的元素(即更改返回的结果)，那么更改 flatten（）展平后的数组，原数组不会受到影响。

但是更改 ravel（）以及reshape（-1）展平后的数组，原数组会受到影响。

 

 

 

 

 

 

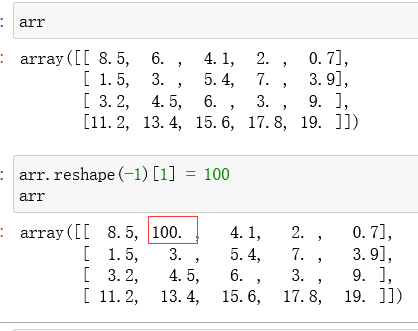
但是注意，仅使用三个函数展平数组，是不会更改原数组的。

 

3）将多个数组合并为一个更大的数组

 

 

现在使用 np.hstack（）函数将这两个二维数组（3行4列 以及 3行5列）横向合并为一个3行9列的二维数组：

 

 

使用 np.vstack（）将arr1（3行4列）以及 arr3（4行4列）纵向合并为1个 7行4列的二维数组：

 

 

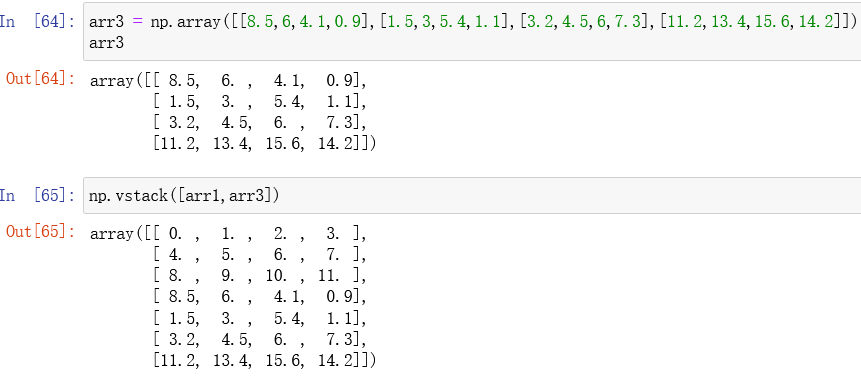
还可以使用 np.concatenate()函数来合并数组，有两个参数，第一个参数是一个元组，代表要合并的数组；第二个参数是 axis，当axis = 0 时，表示沿着行的方向进行操作（纵向合并）；当axis = 1 时，表示沿着列的方向进行操作（横向合并）。

 

 

 

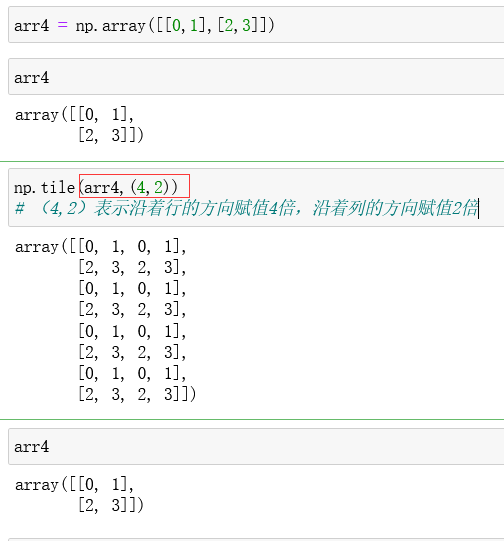
使用 np.tile() 来进行复制扩展二维数组。有两个参数，第一个参数是原数组，第二个参数是复制的倍数。该操作不会改变原数组。

 

 

 

三维数组：

 

 

 

 

 

▲数组的通用函数和广播机制

 

 

 

▲python广播运算机制:

 

 

如上图所示，两个同型二维数组相加，正常相加。

但是，如果是不同型的数组相加，也可以相加，如下图所示：

 

 

这是因为python会使用广播机制：

 

 

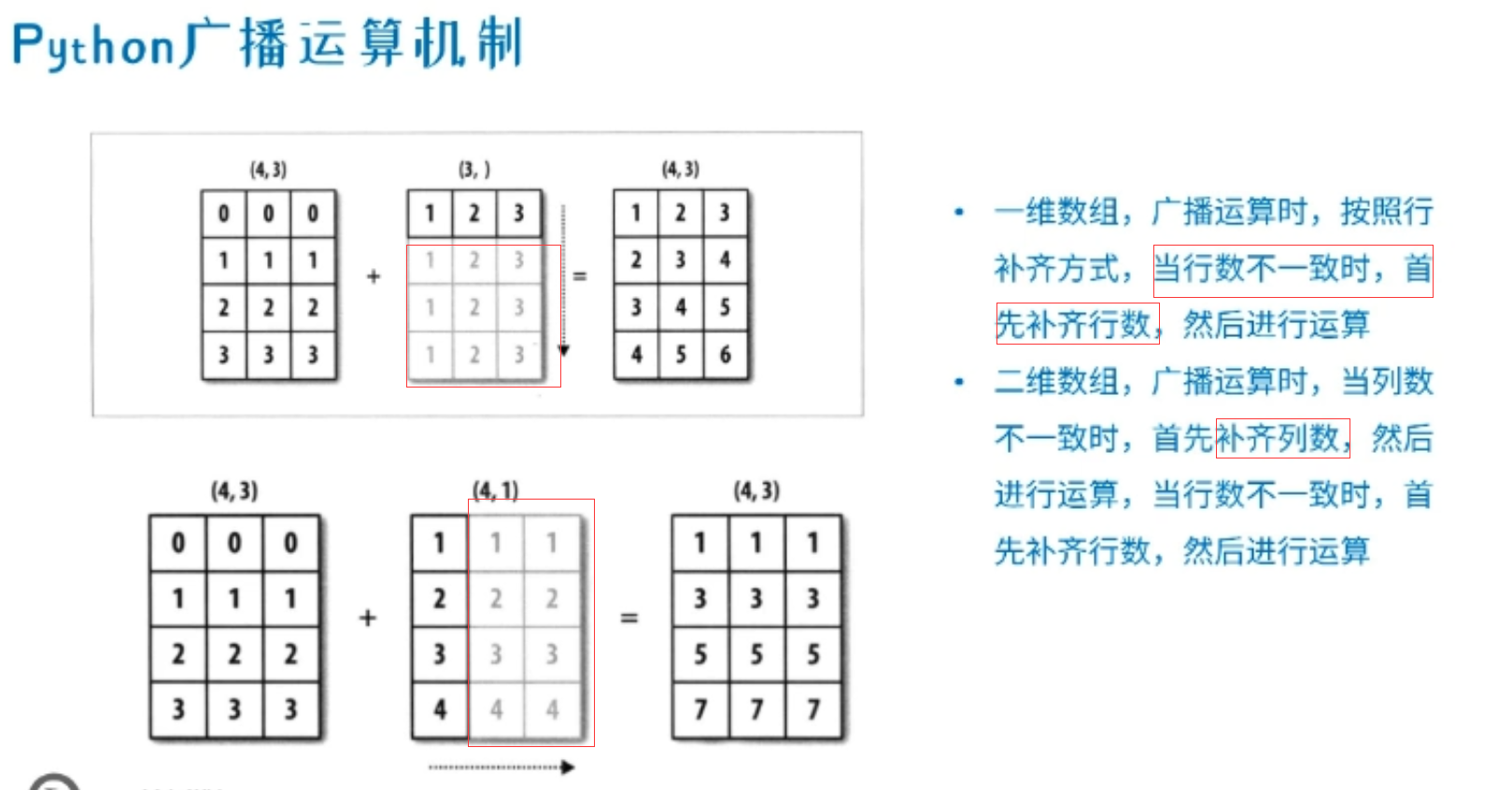
注意，补齐并不是补0.

列补齐方式：

 

 

行补齐方式：

 

 

如果两个不同型数组相加时，如果能够行、列补齐则补齐后相加，否则会报错。

 

▲通用函数运算

 

 

 

 

 

 

 

np.add（）函数：

np.add（）函数也会使用广播机制。add（）函数只能同时支持两个数组相加。

 

np.subtract（）：

 

 

np.multiply（）：

 np.power（）：对数组求幂（数组中的每个元素都求幂）

np.unique（）：去重复

np.in1d（a,b）:分别判断数组a中的每个元素是否在数组b中(注意函数中是数字1不是字母  l )

 

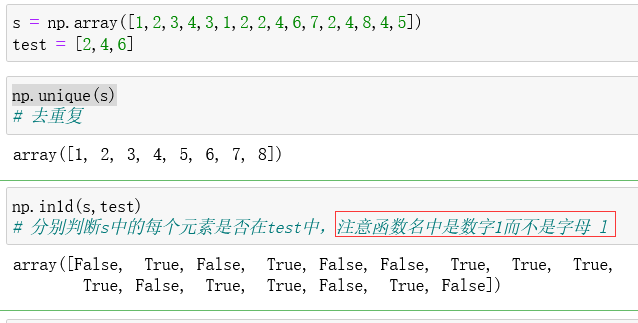
 np.intersect1d(a,b)：返回a，b交集，同样函数名中是数字 1 不是字母 l

 

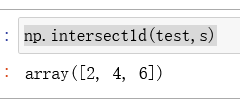
np.equal(a,b) 和 == ：比较运算：（不同型数组比较时会执行广播机制）

 

np.greater(a,b) 与 > :比较大小

 

any（）：只要有一个返回True 就返回 True

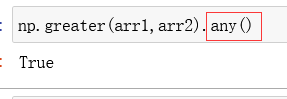
 all（）：所有都返回True时才返回True

 

numpy中的空值none 是 np.nan,对空值进行判断的函数 是 np.isnan()函数：

 

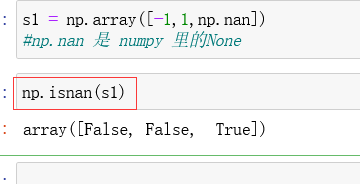
在数据分析时，能用numpy函数就用numpy函数，因为效率比较高。

 

▲搜索与排序

 

 

排序函数中,sort（）返回的是排序后的结果；argsort（）返回原来数组中从小到大的索引值。

同时，使用 sorted() 函数也可以进行排序。

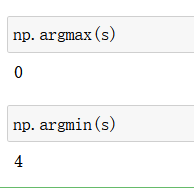
np.argmax（）函数返回最大的元素的索引

np.argmax（）函数返回最小的元素的索引

 

 

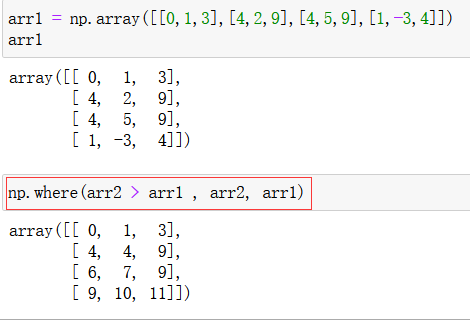
np.where(a,b,c)返回一个数组。

a是bool值，如果是True的话，返回结果b，如果是false的话，返回结果c

 

np.extract（a，b）函数：a是一个bool值， 只有当a为True时才会将b的值提取出来

 

 

三、Numpy运用

 

 

▲Numpy文件读写

 

 

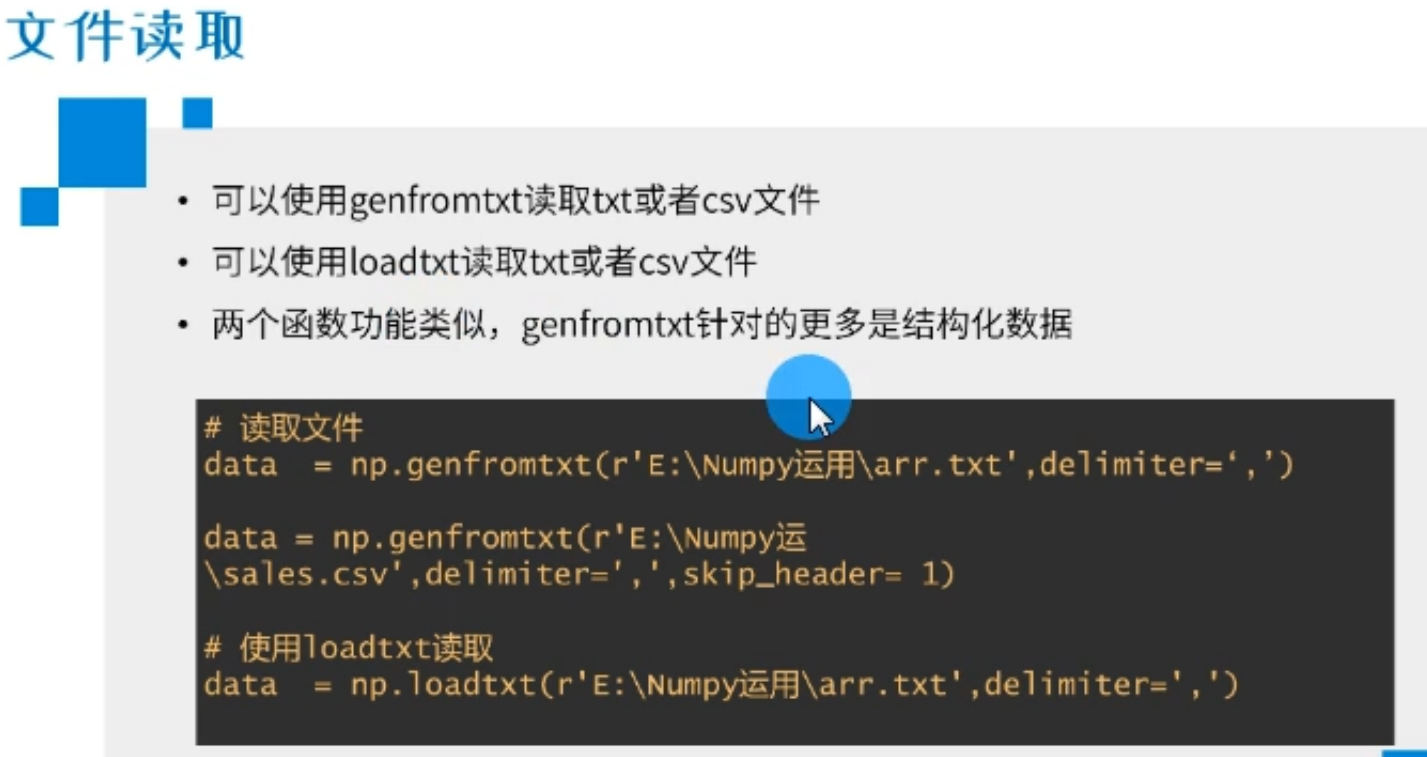
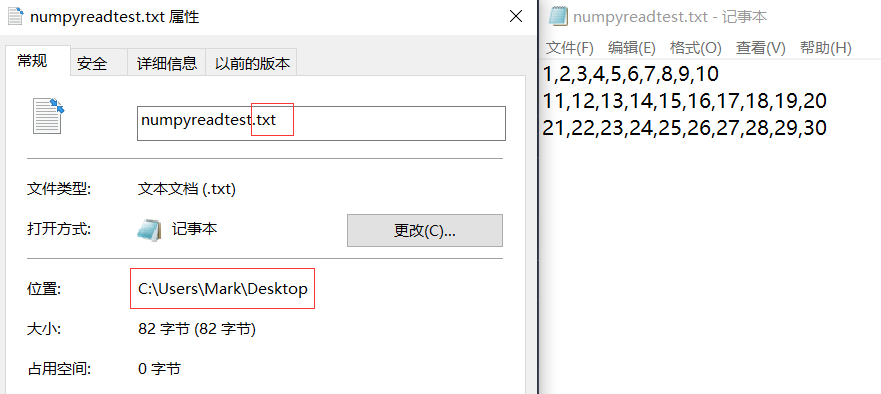
假如有两个文件在桌面：

 

 

 

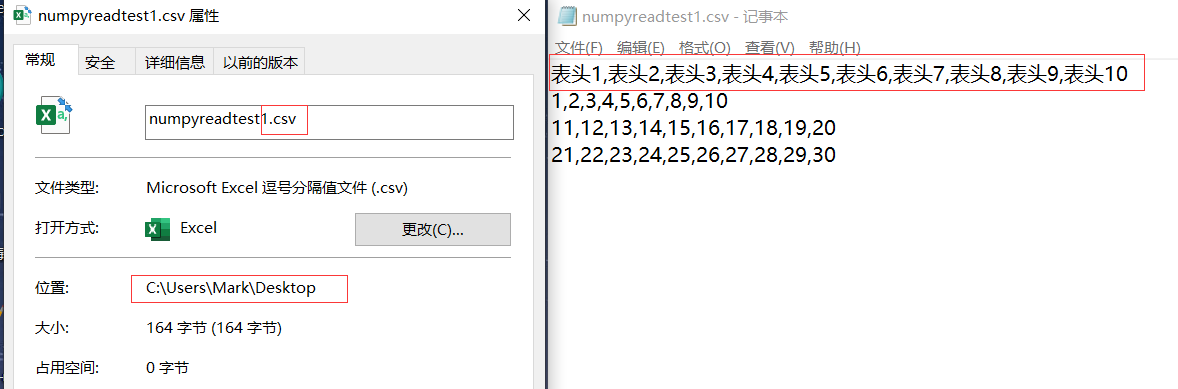
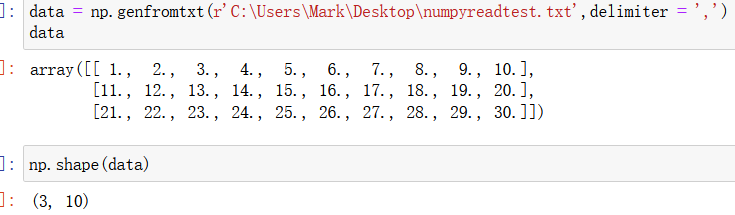
使用np.genfromtxt() 函数读取，该函数的参数可以使用 np.genfromtxt? 来查看，如下：

 

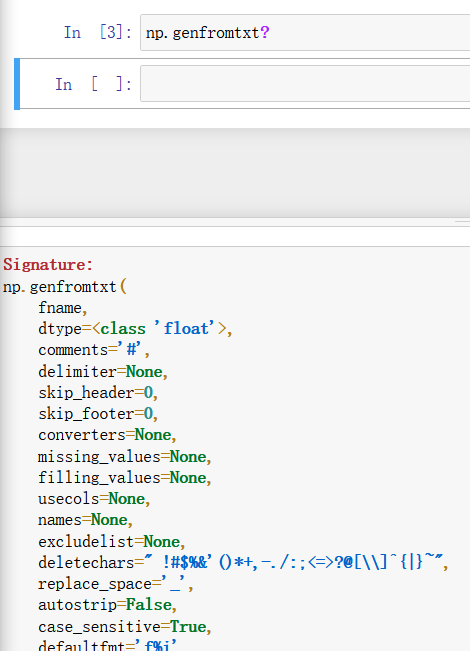
一般在路径前面加上 r 以防有转义字符；delimiter 参数代表文件数据中的分隔符（如上面两个文件中的分隔符就是英文的 逗号, ，如果文件中有表头（如csv文件中的第一行），不想读取表头就用 skip_header = 1 来跳过表头）

读取txt内容如下：

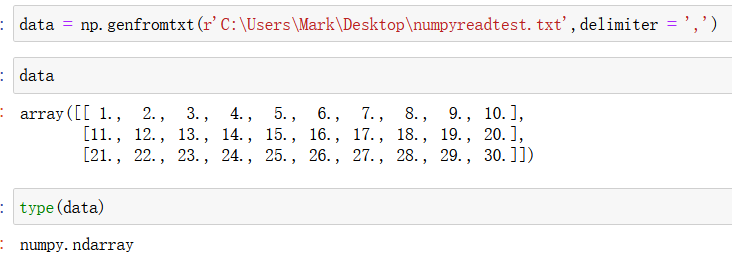
显然读取的结果是一个数组类型，因为是使用np的函数读取的。

读取csv内容如下：

 

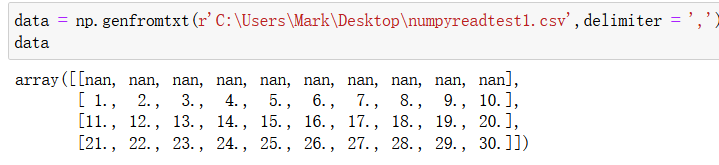
第一行是表头，如果跳过表头只读取数据，使用 skip_header = 1 参数：

 

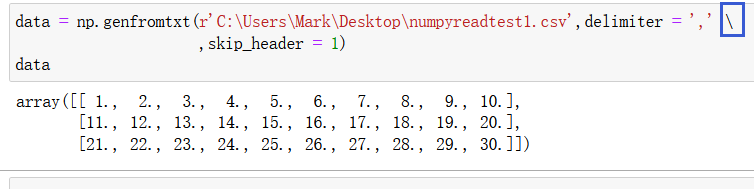
其中 \ 的意义是该行还没有编辑结束。

 

使用 loadtxt（）函数读取文件：

一般我们建议使用 np.genfromtxt（）函数来读取文件，它比 np.loadtxt（）函数的功能要强大一点。

 

 

▲文件存储

将每次数据分析的结果进行保存

使用np.savetxt（）函数来存储数据。

第一个参数是路径，第二个是data，即python本地的数据名称，第三个是delimiter分隔符，第四个 fmt 是存储数据的格式，比如科学计数法 或者 %.3f 为保存为三位小数等等。

 

如上图，执行完后，桌面上出现：

 

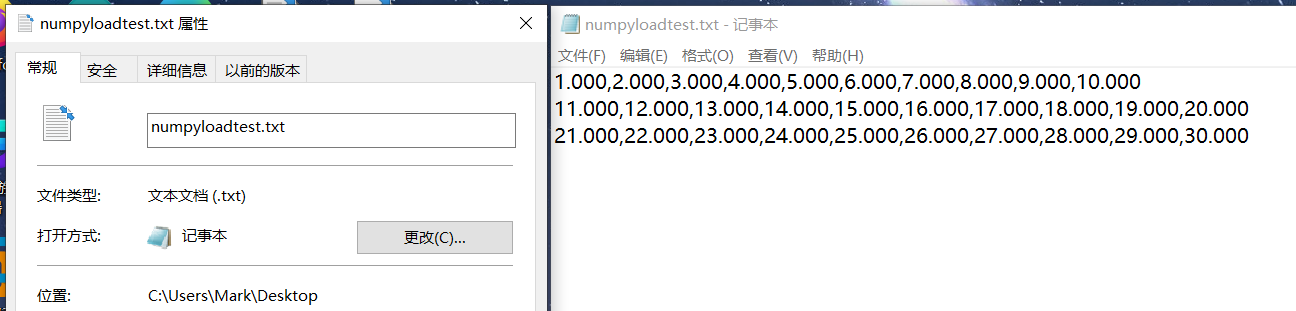
▲Numpy字符串操作

 

 

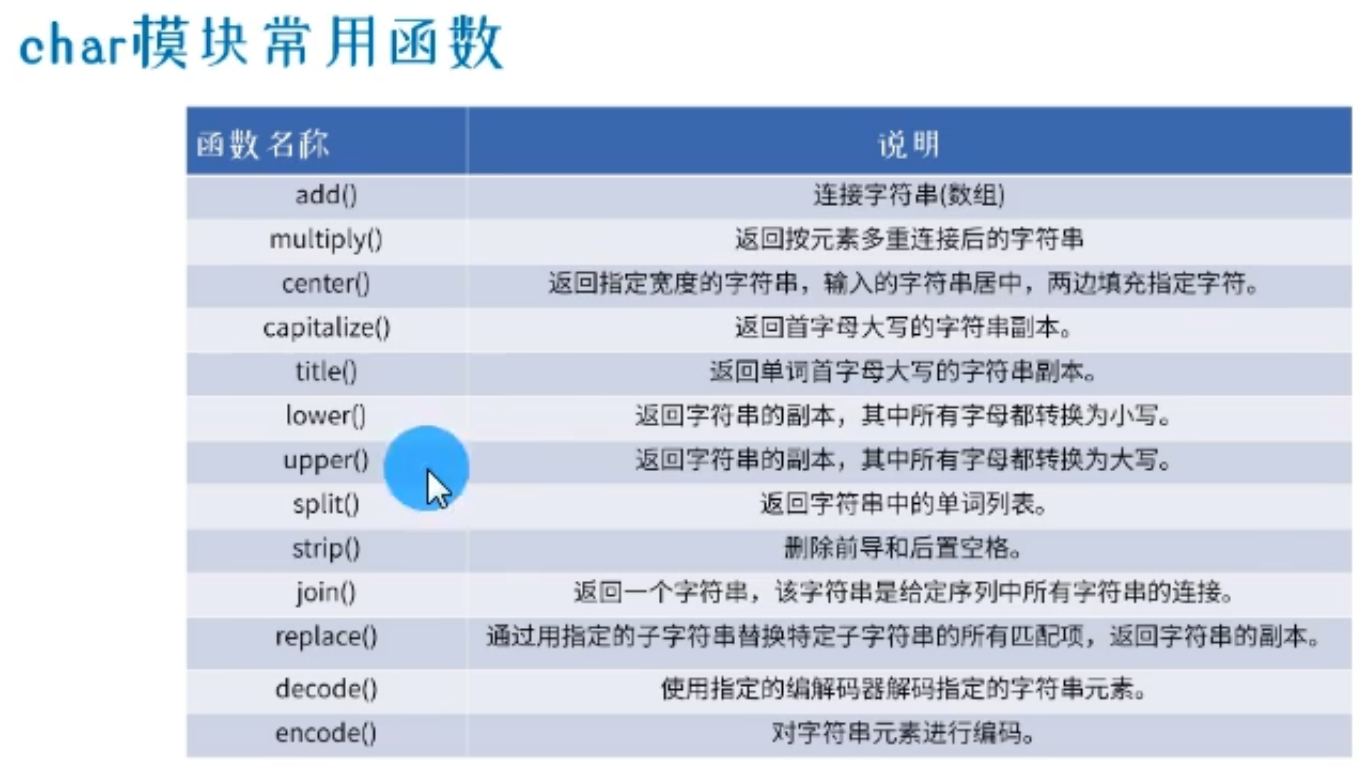
下面是np中 char 模块中 转换大写的函数：

np.char.upper()

注意，参数可以使列表，也可以是数组。但是该函数会返回一个数组格式的数据。

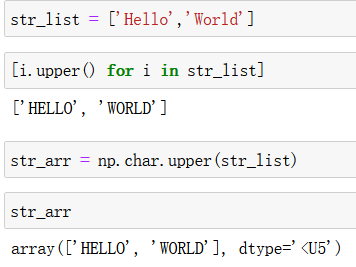
我们建议用np中的函数进行操作而不是写循环，一位 np中的函数与python中的循环效率高很多。

 

add（）：拼接

 

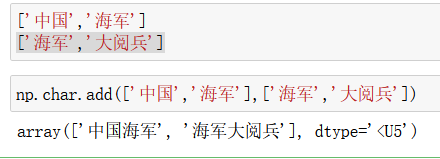
mulitiply（）：重复

 

join（）:以某字符分割

 

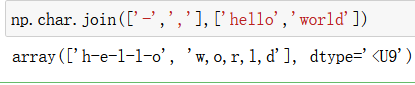
replace（）：替换

 

strip（）：去掉开头或者结尾的某一字符（不能去除中间的）

 

 

▲Numpy统计计算

 

 

1）Numpy随机数生成

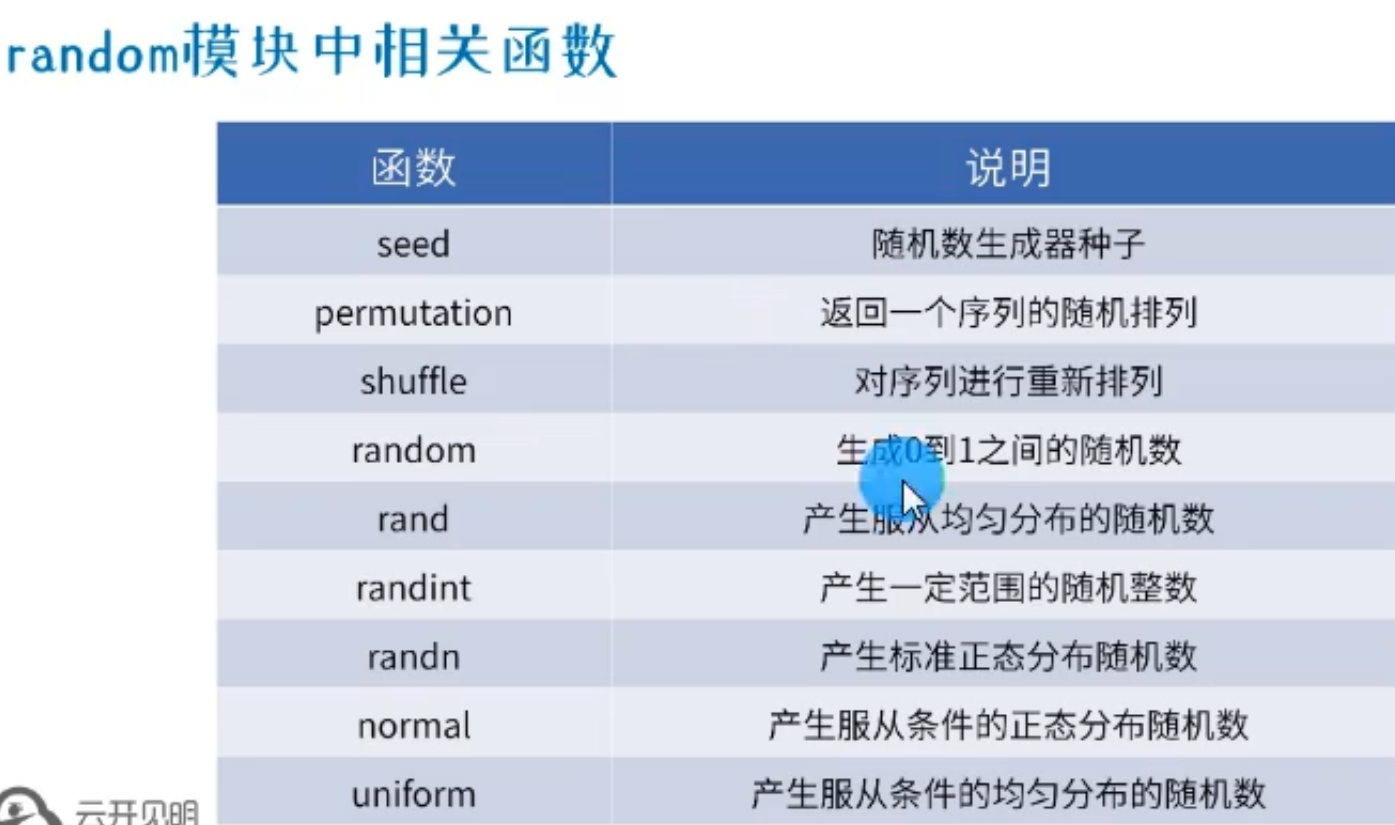
随机数 random 模块是 np下的一个模块

np.random.random():产生0~1之间的随机浮点数

np.random.random(100):产生100个随机浮点数

np.random.random((3,4))或

np.random.random([3,4]):产生一个3行4列的随机数

 

python中产生的是伪随机数，伪随机数依赖于 初始化种子 产生，将初始化种子固定：

 

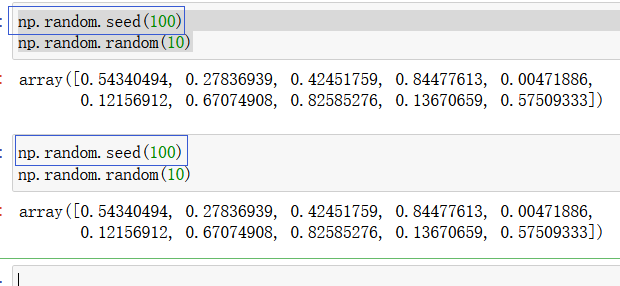
 可以发现，将初始化种子固定后，产生的伪随机数都是一样的了。

 

np.random.randint(a,b,c)：

产生从a到b的整数随机数，共产生c个

 

 

np.set_printoptions(precision = 5):设置产生的随机小数的精度：

 

 

2）Numpy统计相关函数

 

axis = 0 ：沿着行的方向进行操作（竖向操作）

axis = 1 ：沿着列的方向进行操作（横向操作）

 

sum():

 

mean():

 

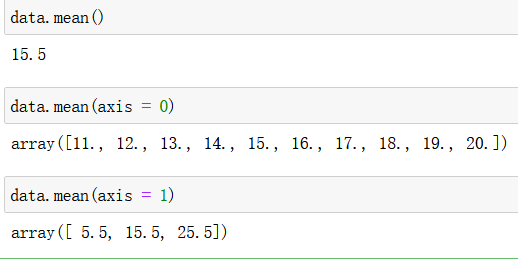
cumsum():累计求和

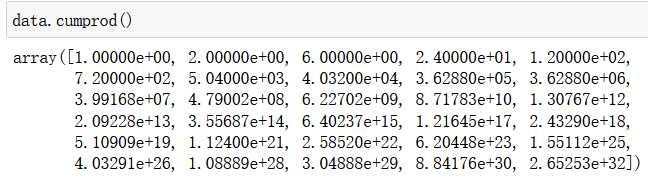
data.cumprod()：累积求积

 

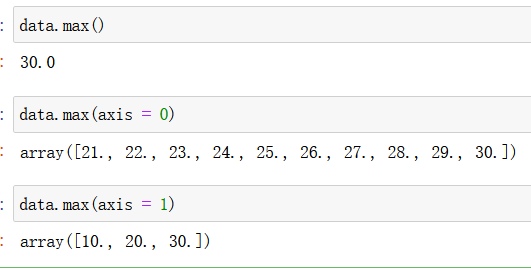
max（）：

 

 

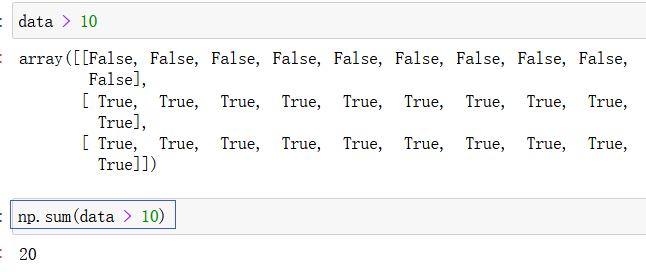
np.sum(data > 10):统计data中有多少大于10的数字

 

 

3）Numpy线性代数

 

 

1）矩阵乘法

注意，一般在python中我们使用 np.matrix() 来创建一个矩阵，但是使用 array也能实现一个矩阵：

 

 

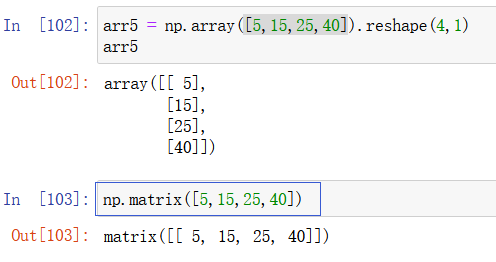
np.dot()

 

两个一维数组相乘，指对应元素相乘并相加。

两个矩阵相乘，要求第一个矩阵的列数等于第二个矩阵的行数，如下图：

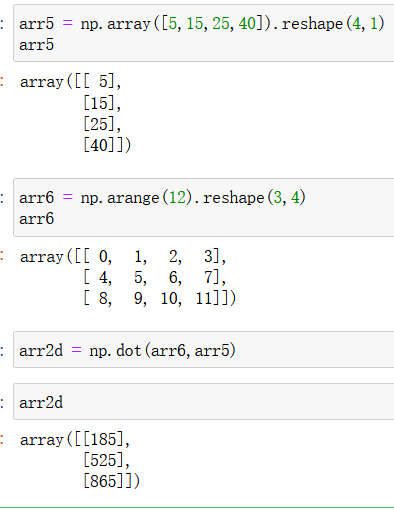
注意，np.dot(arr7,arr8) 和 arr7 * arr8 不一样 ，前者是矩阵乘法，后者只是简单的点乘，即矩阵的对应元素相乘形成一个新矩阵：

 

 

2）矩阵的转置和求逆

矩阵的转置使用 np.transpose(arr)

 

 

矩阵求逆使用 np.linalg.inv(arr) ，注意只有方阵才有逆矩阵

 

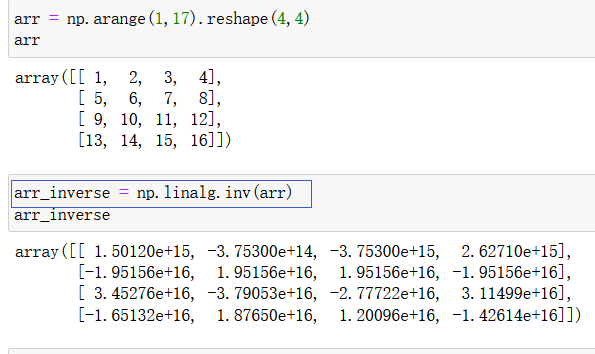
np.diag(arr)：取出矩阵对角线元素

 

 

3）多元一次方程组求解