后缀自动机 (SAM) 学习笔记

定义

后缀自动机（\(\text{Suffix Automaton}\)，简称 \(\text{SAM}\)）是一种用于字符串处理的有限状态自动机（\(\text{DFA}\)），它根据母串的所有后缀构建，能识别出母串的所有子串，且构造算法时间复杂度为线性 \(O(n)\)，空间复杂度为 \(O(n|\Sigma|)\)，\(|\Sigma|\) 是字符集大小，这里将 \(|\Sigma|\) 看作常数。

\(\textbf{SAM}\) 的性质

基础性质

• 从后缀自动机的源点开始走到任意节点的路径都对应了母串的一个子串。

  • 考虑母串的一个后缀 \([l,len]\)，该后缀可以由源点走出，则在走出路径的任意位置截断作为新的路径，都可以对应该后缀的某个前缀，即 \([l,r]\quad(r\in[l,len])\)。

• 母串的任一子串都与从源点出发的一条路径对应，且该对应关系是唯一的。即路径不同，形成的子串不同；子串不同，路径不同。

• 后缀自动机的点数与边数都为线性。

边的种类

后缀自动机上有两种边：

• 转移边，和 \(\text{Trie}\) 的构建方式一样，在某个节点表示的所有字符串的结尾加上一个字符连出的边。
• \(\text{Parent}\) 链，表示后缀之间的包含关系，连向该点表示的最短的字符串删去首字母后所有后缀对应的节点状态。这些边可以组成一棵 \(\text{Parent Tree}\)。

\(\textbf{Endpos}\)

定义

一个子串在母串中出现的位置的右端点形成的集合。

例如母串 \(S=\texttt{abbcab}\)，子串 \(T=\texttt{ab}\)，则 \(\text{endpos}(\texttt{ab})=\{2,6\}\)，即 \(T=S[1\sim2],S[5\sim6]\)。

则可以得到，一个 \(\text{endpos}\) 集合可能对应多个子串。

\(\text{SAM}\) 中的一个节点的状态与一个 \(\text{endpos}\) 集合相互对应，所以不存在两个不同节点的状态对应同一个 \(\text{endpos}\) 集合，每个节点对应的 \(\text{endpos}\) 集合互不相同。

性质

记 \(\mathcal {Q}_{T}\) 表示子串 \(T\) 的 \(\text{endpos}\) 集合，\(|T|\) 表示字符串 \(T\) 的长度。

• 若 \(\mathcal{Q}_{T}=\mathcal{Q}_{T'}\) 且 \(|T|\geq |T'|\)，则 \(T'\) 为 \(T\) 的后缀。

  • 对于任意一个右端点位置 \(pos\in \mathcal{Q}_T\)，\(T'\) 也出现在该位置，且长度不大于 \(T\)，根据 \(T=S[pos-|T|+1\sim pos],T'=S[pos-|T'|+1\sim pos],|T|\geq |T'|\)，可以得到 \(T'\) 为 \(T\) 的后缀。

• 对于两个不同子串 \(T,T'\)，设 \(|T|\geq |T'|\)，要么 \(\mathcal{Q}_T \subseteq\mathcal{Q}_{T'}\)，要么 \(\mathcal{Q}_{T}\bigcap\mathcal{Q}_{T'}=\empty\)。根据 \(\text{endpos}\) 的关系也可以反推 \(T\) 与 \(T'\) 的关系。

  • 要么 \(T'\) 是 \(T\) 的后缀，此时 \(T\) 出现的位置 \(T'\) 一定出现，但 \(T'\) 出现的位置 \(T\) 不一定出现，要么 \(T\) 与 \(T'\) 无关。

• 一个 \(\text{endpos}\) 集合对应多个子串，假设所有这些不同子串是 \(T_1,T_2,\cdots,T_{k}\) 且满足 \(|T_1|<|T_2|<\cdots<|T_{k}|\)，此时一定满足 \(|T_i|=|T_{i-1}|+1\)，\(T_{i-1}\) 是 \(T_i\) 的后缀。

  • 例如 \(T_1=\texttt{aba},T_{4}=\texttt{cababa}\) 且满足 \(\mathcal{Q}_{T_1}=\mathcal{Q}_{T_4}\)，可以得到 \(T_2=\texttt{baba},T_3=\texttt{ababa}\) 以及 \(\mathcal{Q}_{T_1}=\mathcal{Q}_{T_2}=\mathcal{Q}_{T_3}=\mathcal{Q}_{T_4}\)。考虑 \(T_1\) 出现的位置集合与 \(T_4\) 出现的位置集合相同以及 \(T_1\) 是 \(T_4\) 的后缀，则 \(T_4\) 所有长度为 \(l\quad (l\in[|T_1|,|T_4])\) 的后缀也一定在这些位置集合出现。

\(\textbf{Parent Tree}\)

根据定义比较难理解，可以考虑下图，母串 \(S=\texttt{aababa}\)。

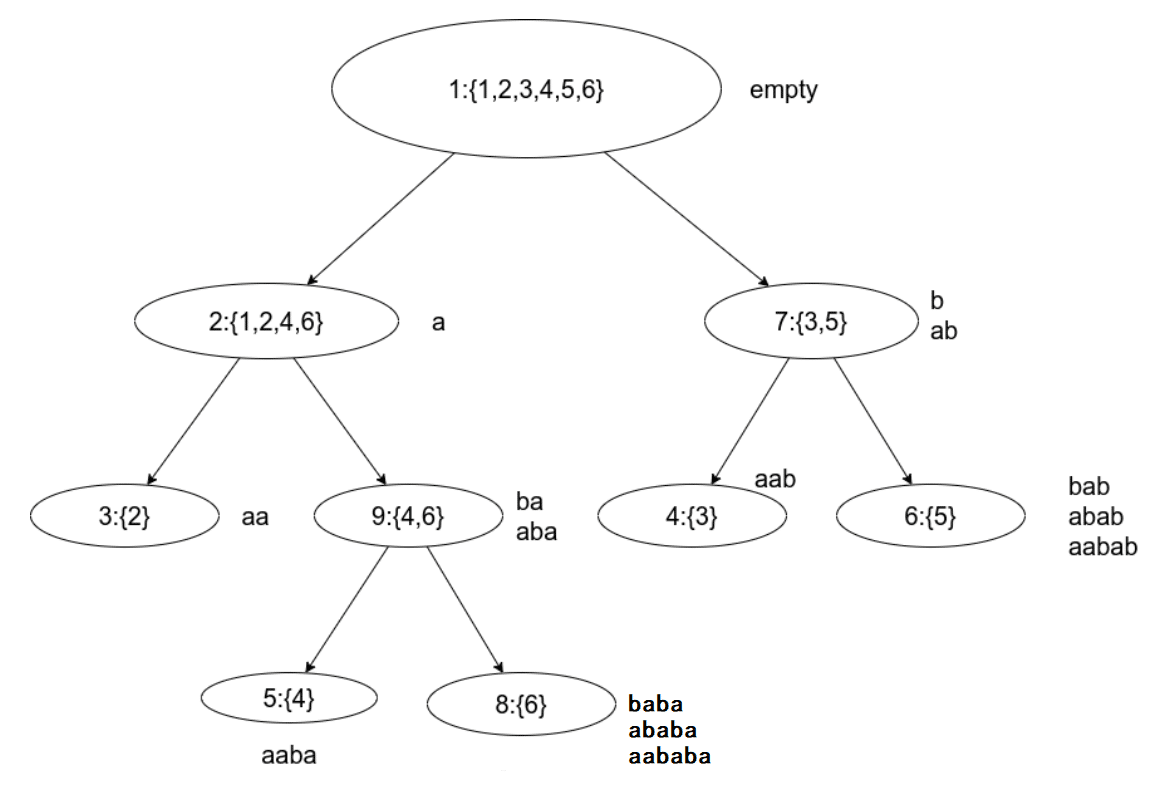
性质

记 \(\mathcal{R}_{T}\) 表示子串 \(T\) 出现但以 \(T\) 为后缀的子串 \(T'\) 都不出现的位置集合，\(\mathcal{U}_{x}\) 表示节点 \(x\) 的 \(\text{endpos}\) 集合，\(\text{Min}_x\) 表示节点 \(x\) 的最短子串，\(\text{Max}_{x}\) 表示节点 \(x\) 的最长子串，\(\text{son}_x\) 表示节点 \(x\) 的子节点构成的点集。

• \(\forall y\in \text{son}_x,|\text{Min}_{y}|=|\text{Max}_x|+1\)。

  • 根据定义，节点 \(y\) 的最短子串删除首字母即得到了节点 \(x\) 的最长子串，每个节点恰好代表若干长度连续的后缀。

• \(\mathcal{U}_{x}=\mathcal{R}_{\text{Max}_{x}}\ \bigcup \ \big{(}\bigcup\limits_{y\in \text{son}_x} \mathcal{U}_{y}\big{)}\)。

  • 显而易见节点 \(x\) 的 \(\text{endpos}\) 集合为子节点 \(y\) 的 \(\text{endpos}\) 集合的父集，且包含节点 \(x\) 自己的子串出现的位置，也就是这些集合的并。

根据这两个性质可以分析出沿着 \(\text{Parent}\) 链向上跳本质上就是不断从后缀中删去前缀的过程，也可以分析出点数最多有 \(2n\) 个（考虑多个子节点的 \(\text{endpos}\) 集合大小越接近时点数越多，也就是等比数列求和），进一步得到边数最多为 \(3n\) 条（\(2n\) 个点的生成树占据 \(2n-1\) 条，母串最多有 \(n\) 个不同的后缀，从源点走到不能再走的点代表一种后缀，最多 \(n\) 条，加起来最多 \(3n\) 条）。

构建后缀自动机

运用增量法构造，假如已经构建完母串的前缀 \(S[1\sim n]\) 的后缀自动机，在此基础上增加第 \(n+1\) 个字符 \(S_{n+1}\) 形成新的后缀自动机。

加入第 \(n+1\) 个字符时一共有 \(3\) 种情况（下面举例时假设已经构建好 ab 的后缀自动机）：

• 不论哪种情况，首先将对应 \(S[1\sim n]\) 的节点连出一条新边，边上字符为 \(S_{n+1}\)，也就是在末端加入一个新字符。

• 不断在 \(\text{Parent Tree}\) 上向上跳，直到存在一个和 \(S_{n+1}\) 一样的出边。

• abc - 加入字符 c 时，跳到了源点都没有字符 c 的出边，此时将跳的时候经过的点连一条字符为 c 的边向新点即可，在 \(\text{Parent Tree}\) 上将新点父亲设为源点。

• aba - 加入字符 a 时，跳到了源点才发现有字符 a 的出边，记跳到源点前的一个点为 \(f\)，源点连出字符 a 的出边到达的点为 \(q\)，则 \(f\) 是连向新点的最短子串的点，满足 \(|\text{Min}_{new}|=|\text{Min}_{f}|+1\)，判断 \(q\) 的最长子串是否由源点转移而来，此种情况下是，所以 \(|\text{Max}_{q}|=|\text{Max}_{源点}|+1\)。且源点在 \(\text{Parent Tree}\) 上是 \(f\) 的父亲，所以满足 \(|\text{Min}_{f}|=|\text{Max}_{源点}|+1\)。推出 \(|\text{Min}_{new}|=|\text{Min}_{f}|+1=(|\text{Max}_{源点}|+1)+1=|\text{Max}_{q}|+1\)，所以将 \(new\) 在 \(\text{Parent Tree}\) 上的父亲设为 \(q\) 即可。

• abb - 加入字符 b 时，跳到了源点才发现有字符 b 的出边，但此时 \(q\) 的最长子串不由源点转移，而是由另一点 \(t\)（这个例子中 \(t\) 是 \(\{\texttt a\}\)）转移 ，此时 \(q\) 一部分由源点转移，一部分由 \(t\) 转移，将 \(q\) 分裂为 \(xq\) 和 \(yq\)，各自都保留 \(q\) 的出边，其中 \(xq\) 是由源点转移而来的，\(yq\) 是由 \(t\) 转移而来的，显然 \(yq\) 为 \(xq\) 的后缀，于是将 \(yq\) 在 \(\text{Parent Tree}\) 上的父亲设为 \(xq\)，再将 \(new\) 在 \(\text{Parent tree}\) 上的父亲也设为 \(xq\) 即可。

该例子不仅包含了该后缀自动机的构建，也包含了总体的三种情况，实现时按照三种情况分类讨论即可。

代码实现

struct Node{
	int son[26],len,fa;
	Node(){ memset(son,0,sizeof son); len=fa=0; }
} node[N<<1];
int last=1,tot=1; //last 表示前缀 S[1~n] 的节点，tot 表示 SAM 的总节点数
inline void add(int c){
	int p=last,nw=last=++tot; node[nw].len=node[p].len+1; //新建一个节点
	for (; p&&!node[p].son[c]; p=node[p].fa) node[p].son[c]=nw; //跳父链将节点的出边连向新节点
	if (!p) node[nw].fa=1; //情况1: 源点
	else {
		int q=node[p].son[c];
		if (node[q].len==node[p].len+1) node[nw].fa=q; //情况2: p -> q
		else {
			int xq=++tot; //情况3: t -> q
			node[xq]=node[q]; node[xq].len=node[p].len+1; node[q].fa=node[nw].fa=xq;
			for (; p&&node[p].son[c]==q; p=node[p].fa) node[p].son[c]=xq;
		}
	}
}