实验文档3

关于第三次实践课作业

实验结论

task1.c

#define _CRT_SECURE_NO_WARNINGS
#include<stdio.h>
char score_to_grade(int score);
int main() {
    int score;
    char grade;

    while (scanf("%d", &score) != EOF)
    {
        grade = score_to_grade(score);
        printf("分数 : %d , 等级 : %c\n\n", score, grade);
    } 
    return 0;
}
char score_to_grade(int score) {
    char ans;
    switch (score / 10) {
    case 10:
    case 9:ans = 'A'; break;
    case 8:ans = 'B'; break;
    case 7:ans = 'C'; break;
    case 6:ans = 'D'; break;
    default:ans = 'E';
    }
    return ans;
}

question1:函数 score_to_grade 的功能是什么？形参类型、返回值类型是什么？

answer1：函数的功能是将得到的分数通过计算转化为对应的等级；

形参类型是int型数据，返回类型是字符型数据；

question2：如果line21-28以下形式，有问题吗？如果有，指出有哪些问题？ 

switch(score/10) {
 case 10:
 case 9:   ans = "A"; 
 case 8:   ans = "B";
 case 7:   ans = "C";
 case 6:   ans = "D";
 default:  ans = 'E';
}

answer2:有问题;

没有使用break语句会导致ans得到对应grade时

无法离开switch语句，返回ans时其值始终是E

 

 

task2.c

#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
int sum_digits(int n);

int main()
{
    int n;
    int ans;
    while (printf("Enter n:"), scanf("%d", &n) != EOF) {
        ans = sum_digits(n);
        printf("n = %d,ans = %d\n\n", n, ans);
    }
    return 0;
}
int sum_digits(int n) {
    int ans = 0;
    while (n != 0) {
        ans += n % 10;
        n /= 10;
    }
    return ans;
}

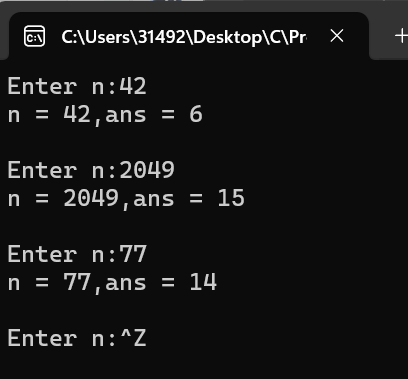
question1：函数 sum_digits 的功能是什么？

answer1：取出n的各个数位，并将它们相加

question2：如果保持 main 代码和函数 sum_digits 声明不变，

把函数 sum_digits 定义成如下 实现方式，能实现同等的效果吗？

如果不能实现同等效果，分析原因。

如果能实现同等效果，说明两种实现方式背后的算法思维区别。 

int sum_digits(int n) {
 if(n < 10)
     return n;
 return sum_digits(n/10) + n%10;
}

answer2：能实现同等效果

第一种算法思维是迭代，

通过取余取出n的个位后通过整除去掉n的个位

如此往复不断得到n的个位并累加

第二种算法思维是递归，

最简单情形即是n本身就是一个个位数，

即可以直接返回n值；

其他情况下：既通过取余得到n的个位数，

又通过取整去掉n的个位进入函数作进一步计算

 

 

task3.c 

#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
int power(int x, int y);
int main() {
    int x, n, ans;
    while (printf("Enter x and n:"), scanf("%d %d", &x, &n) != EOF) {
        ans = power(x, n);
        printf("n = %d,ans = %d\n\n", n, ans);
    }
    return 0;
}
int power(int x, int n) {
    int t;
    if (n == 0) {
        return 1;
    }
    else if (n % 2) {
        return x * power(x, n - 1);
    }
    else {
        t = power(x, n / 2);
        return t * t;
    }
}

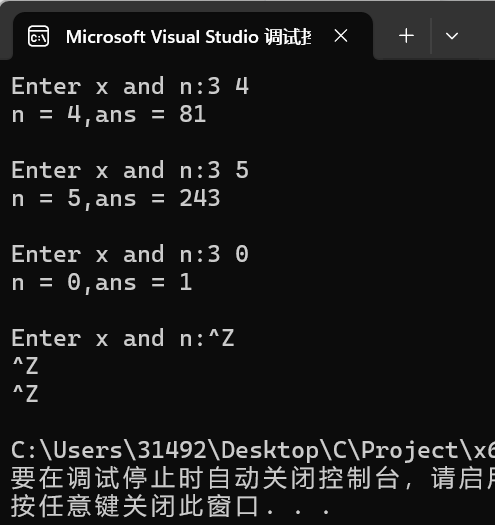
question1：函数 power 的功能是什么？

answer1：计算x的n次幂

question2：函数 power 是递归函数吗？如果是，找出递归模式。写出这个递归模式对应的数学公 式模型

answer2：是,其递归模式是：

 

 

 

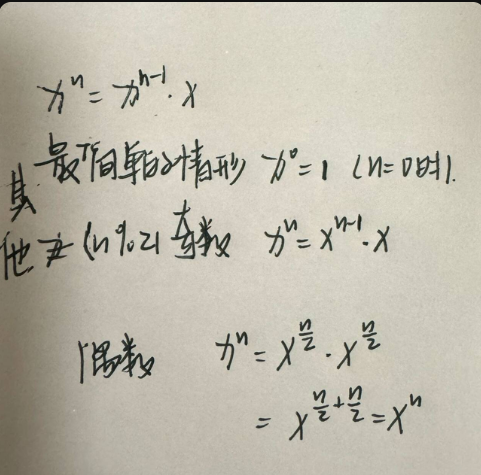
task4.c

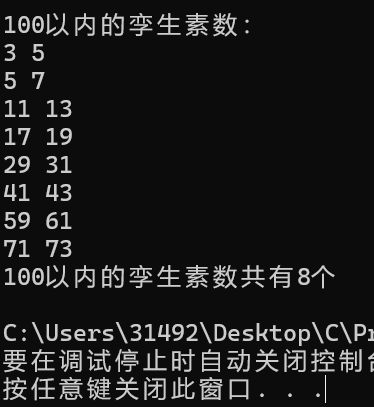
#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
#include<math.h>
int is_prime(int x);
int main()
{
    printf("100以内的孪生素数：\n");
    int cnt = 0;
    int i ;
    for (i = 2; i <= 100; i++) {
        if (is_prime(i) == 1 && is_prime(i + 2) == 1) {
            printf("%d %d\n", i, i + 2);
            cnt++;
        }
    }
    printf("100以内的孪生素数共有%d个\n", cnt);
    return 0;
}
int is_prime(int x) {
    int i;
    for (i = 2; i <= sqrt(1.0*x); i++) {
        if (x % i == 0) {
            return 0;
        }
    }
    return 1;
}

 

 

 task5.c

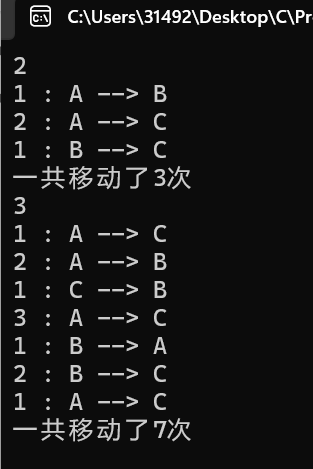
#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
void hanoi(int n, char from, char temp, char to);
void move(int n, char from, char to);
int cnt = 0;
int main() {
    int n;
    while (scanf("%d", &n) != EOF) {
        cnt = 0;
        hanoi(n, 'A', 'B', 'C');
        printf("一共移动了%d次\n", cnt);
    }
    return 0;
}
void hanoi(int n, char from, char temp, char to) {
    if (n == 1) {
        move(n, from, to);
    }
    else {
        hanoi(n - 1, from, to, temp);
        move(n, from, to);
        hanoi(n - 1, temp, from, to);
    }
}
void move(int n, char from, char to) {
    printf("%d : %c --> %c\n", n, from, to);
    cnt++;
}

 

 

task6_1.c

用迭代方式实现计算组合数 func() 

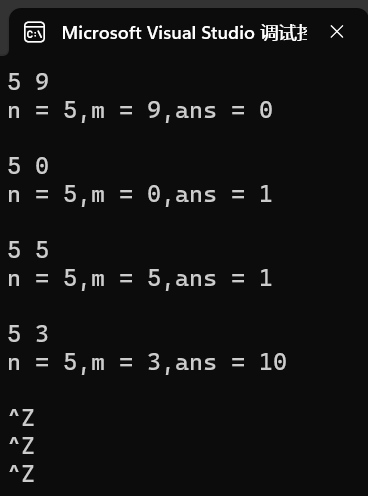
#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
int func(int n, int m);
int fac(int n);
int main()
{
    int n, m;
    int ans;
    while (scanf("%d %d", &n, &m) != EOF) {
        ans = func(n, m);
        printf("n = %d,m = %d,ans = %d\n\n", n, m, ans);
    }
    return 0;
}
int func(int n, int m) {
    return fac(n) / (fac(m) * fac(n - m));
}
int fac(int n) {
    int i,ans=1;
    for (i = 1; i <= n; i++) {
        ans *= i;
    }
    return ans;
}

task6_2.c

用递归函数实现计算组合数 func() 

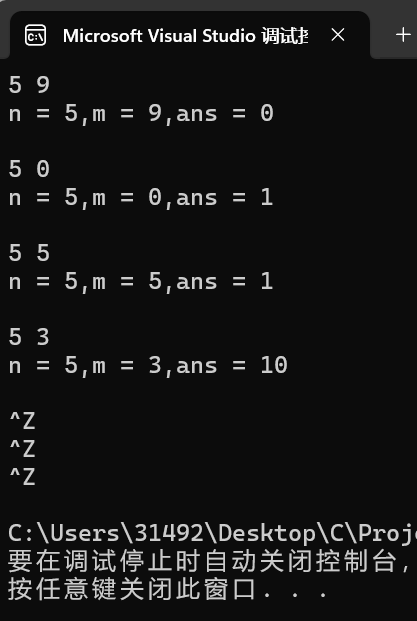
#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
int func(int n, int m);

int main()
{
    int n, m;
    int ans;
    while (scanf("%d %d", &n, &m) != EOF) {
        ans = func(n, m);
        printf("n = %d,m = %d,ans = %d\n\n", n, m, ans);
    }
    return 0;
}

int func(int n, int m) {
    if (n == 0 && m!=0) {
        return 0;
    }
    else if (m == 0) {
        return 1;
    }
    else {
        return func(n - 1, m) + func(n - 1, m - 1);
    }
}

 

 

task7.c

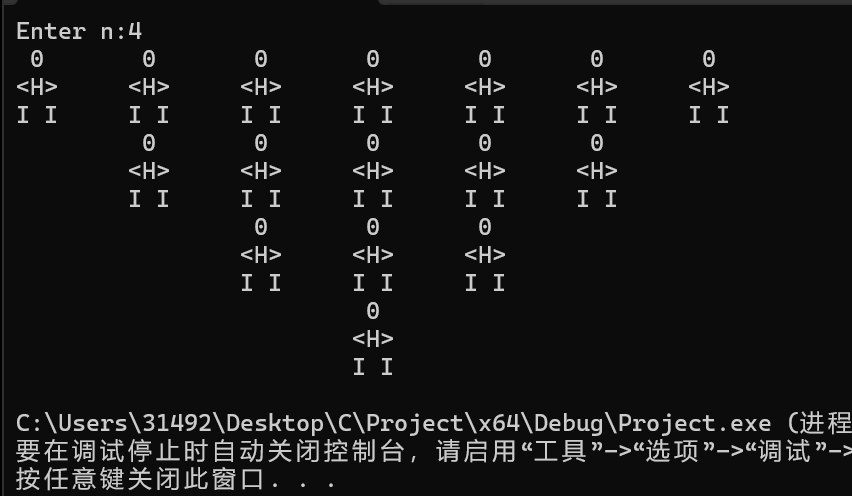
#define _CRT_SECURE_NO_WARNINGS
#include<stdio.h>
void print_charman(int n);
void one(int x);
void two(int x);
void three(int x);
int main()
{
    int n;
    printf("Enter n:");
    scanf("%d", &n);
    print_charman(n);
    return 0;
}
int j, cnt = 0;
void print_charman(int n) {
    int i;
    for (i = n; i >= 1; i--) {
        int x = (2 * i)- 1;
        one(x);
        two(x);
        three(x);
        cnt++;
    }
    
}

void one(int x) {
    for (j = 1; j <= cnt; j++) {
        printf("\t");
    }
    int i;
    for (i = 1; i <= x; i++) {
        printf(" 0\t");
    }
    printf("\n");
}
void two(int x) {
    for (j = 1; j <= cnt; j++) {
        printf("\t");
    }
    int i;
    for (i = 1; i <= x; i++) {
        printf("<H>\t");
    }
    printf("\n");
    
}
void three(int x) {
    for (j = 1; j <= cnt; j++) {
        printf("\t");
    }
    int i;
    for (i = 1; i <= x; i++) {
        printf("I I\t");
    }
    printf("\n");
}

 

实验总结

1.尚存的问题 ：对于Hanoi塔的理解问题，无法正确理解两个函数

　　　　　　　对于全局变量，局部变量等的理解

　　　　　　　编写递归函数

2.函数作为一种模块化程序的设计手段，

在编写一个“大”程序时可以逐个编写每个“小”程序（即函数）

逐一进行调试纠错，保证每个函数都是正确的，

这样在运用函数时可以保证不因局部函数的问题

而影响整体程序，使调适时更加便捷清晰