密码学之公钥密码算法
公钥密码算法简介
公钥密码算法在加密和解密中使用一对不同的密钥，其中一个密钥公开，称为公钥，宁一个密钥保密，称为私钥，且由公钥求解私钥计算是不可行的的。顾名思义，公钥是公开的。
RSA公钥密码体制
简介
是迄今为止理论上最为成熟完善的公钥密码体制。也是目前广泛应用的公钥密码体制。RSA的基础是数论的欧拉定理，他的安全性依赖于大整数因子分解的困难。
数学知识补充
互质
如两个正整数，除了1之外就没有其他公因子，就称这两个正整数是互质的。而且并没有要求这两个正整数都是质数，如15和4就是互质的。
欧拉函数
是求小于x并且和x互质的数的个数。其通式为φ(x) = x(1-1/p1)(1-1/p2)...(1-1/pₙ)，其中p1，p2..pn为x的所有质因数，x为不为零的整数。
比如x=16时φ(16) = 16 * (1-1/2) = 8
我们也可以列举与16互质，且小于16的数: 1,3,5,7,9,11,13,15,个数为8个
而在RSA求密钥对中就需要用到欧拉函数的一个性质，即如果p是素数的话，φ(p)=p-1。
模反元素
如果两个正整数a和b互质，那么一定可以找到整数n，使得ab-1被n整除，或者说ab被n整除的余数是1。一般在已知其中一个整数假如是a和整数n的情况下，求另一个整数b的运算就是模反运算。
其解法包括朴素算法，辗转相除法，欧几里得算法。
RSA生成公钥私钥对
-
选取两个不同的大素数p和q
-
计算n=p*q,并计算n的欧拉函数φ(n)=(p-1)(q-1),也就是求小于n且与n互质的数。
-
随机选取正式e<Z,1<e<φ(n)作为公钥之一，且要满足e与φ(n)互质。
-
采用模反算法计算私钥d，使ed=1(modφ(n))，也就是d=e⁻¹(modφ(n))，也就是(ed-1)能被φ(n)整除
-
得到公钥(e,n)和私钥d
加密过程
RSA的加密函数很简单，对于明文m，公钥(e,n)，E(m)=mᵉ(modn)
解密过程
RSA的解密过程也很简单移动，对于密文c，私钥d，D(c)=cᵈ(modn)
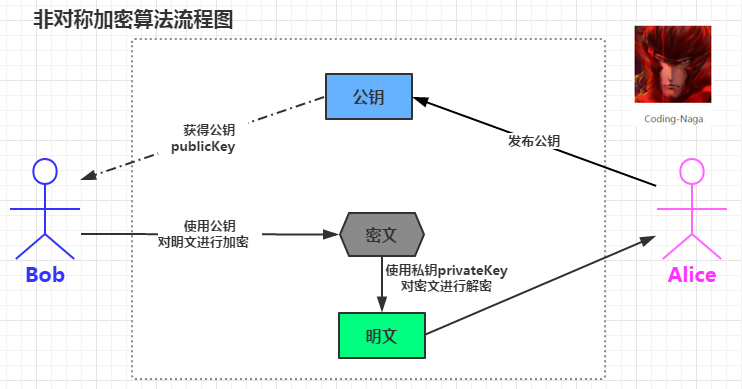
使用流程
