dp深入与进阶(2)：特殊的dp优化:斜率优化(无例题解析版)

斜率优化

\(01.\)应用范围:\(f_i=min/max(a_i \times b_j+c_i+d_j)\)这类递推方程式的时间优化

\(02.\)前置推导:

对于\(f_i=min_j(a_i \times b_j+c_i+d_j)\)

其中满足\(b\)单调递增

假设一值\(j_1\)在\(dp\)中的作用优于\(j_2\)

则有:

\(a_i \times b_{j_2}+d_{j_2}≥a_i\times b_{j_1}+d_{j_1}\)

可得到:

\(a_i≤\frac{(-d_{j_1})-(-d_{j_2})}{b_{j_1}-b_{j_2}}\)

在平面直角坐标系中 令\(x_j={b_j}\)，\(y_j=-d_j\)

则\(k(j_1,j_2)=\frac{(-d_{j_1})-(-d_{j_2})}{b_{j_1}-b_{j_2}}\)

显然可知\(a_i≤k(j_1,j_2)\)时,始终满足\(j_1\)的函数值优于\(j_2\)

从而得到结论:

对于坐标系中横坐标单调递增的\(j_1\)和\(j_2\)

当\(a_i≤k(j_1,j_2)\)时\(,f(j_1)\) 优于 \(f(j_2)\)

反之,有\(f(j_2)\) 优于 \(f(j_1)\)

\(03.\)定理雏形证明:

重要定理:对于三个点 A, B, C,假设横坐标递增,且\(k(A,B)>k(B,C)\),可以证明:\(B\)的函数值一定不最优

证明:(不考虑\(a=k\))

为了方便叙述,令\(k_1=k(A,B),k_2=k(B,C)\)

初始图:

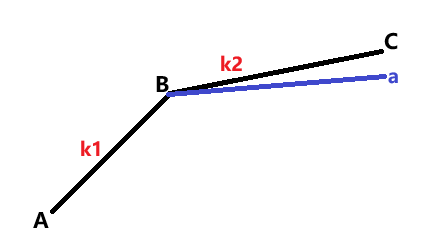
1.假设\(a<k_2<k_1:\)

如图,有\(f(A)>f(B)>f(C)\)

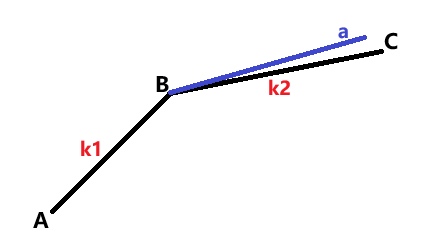
2.假设\(k_2<a<k_1:\)

如图有\(f(A)>f(B)\)且\(f(C)>f(B)\)

3.假设\(k_2<k_1<a:\)

如图有\(f(C)>f(B)>f(A)\)

可以发现:无论何种情况，\(B\)点一直不是最优的点,所以\(dp\)过程中可以不考虑\(B\)点

由此得证

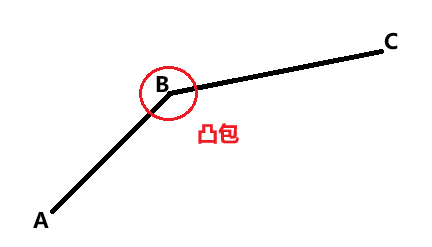
从几何意义上看:如果在建好的的坐标系中发现“上凸包”（“凸包”如上图所示）,则凸包的顶点一定不是最优点

\(04.\) 斜率优化的定义:

\(dp\)中忽略所有“上凸包”,优化时间复杂度的优化办法,这样的优化方法即为斜率优化

显然,一个没有上凸包的图\(k\)值一定是单调递减的

所以优化时可以维护一个单调递减的队列来实现

05.一种可行的代码写法

// 计算两点之间的斜率
int slope(int j, int k) 
{
    int x = (f[j] - f[k] + s[j] * s[j] - s[k] * s[k]) / (s[j] + s[k]);
    return x;
}
for (int i = 1; i <= n; i++) 
{
  while (L < R && slope(q[L], q[L + 1]) <= s[i]) L++; // 维护下凸包
    dp[i] = dp[q[L]] + (s[i] - s[q[L]]) * (s[i] - s[q[L]]) + m; // 更新dp值
  while (L < R && slope(q[R - 1], q[R]) > slope(q[R], i)) R--; // 剔除无效点
    q[++R] = i; // 将当前点加入队列
}

最后扔两道例题在这里,下一篇文章或下下篇文章会进行进一步解析

例\(1:P3195\)

例\(2:P2900\)