插入排序
插入排序,和我们打扑克牌是一个道理。刚开始时,手里只有一张牌,它肯定是排序好的。后来,来了第二张牌,它和第一张牌进行比较,插入到合适的位置。再后来,来了第三张牌,它和手里的两张牌进行比较,插入到合适的位置。可以发现,插入排序分为两个部分,一部分是排序好的部分,一部分是未排序好的部分。当从未排序好的部分来了一个数据后,它要在排序好的数据中找到一个合适的位置,并插入,使排序好的部分仍然是排序好的,不会打乱以前的排序。
如果以数组来组织数据的话,数组也可以分为两个部分,数组中第一个元素和数组中剩下的部分。数组中的第一个元素,由于只有一个元素,它是排序好的,数组中剩下的部分,它们是未排序好的。如果拿出第二个元素和第一个元素进行比较,排序好,那么,数组中第一个元素和第二个元素为排序好的部分,剩下的部分则是未排序的部分。第三个元素就要和第一第二个元素进行比较,插入到合适的位置,那么前三个元素就是排序好的,剩下的部分就是未排序的部分。顺着数组的索引依次向后,拿出一个元素和前面排序好的部分进行比较插入,直到数组最后一个元素。假设数组{8, 2, 6, 4, 9, 7, 1}
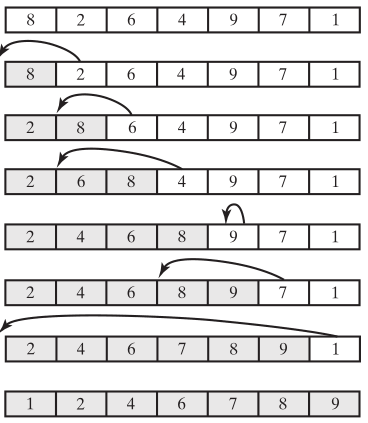
从未排序好的部分拿出一个元素,怎么和前面排序好的部分进行比较,插入呢?因为是排序好的,可以从后向前遍历排序好的部分(数组),如果排序好的元素大于未排序好的元素,排序好的元素向后移一个位置, 为未排序好的元素腾出位置,如果排序好的元素小于未排序好的元素,位置找到了,插入即可。
刚开始的时候,数组排序好的部分只包含索引0处的元素,剩下的部分都是未排序好的部分。从未排序好的部分拿出一个元素,就是遍历数组,数组索引加1,就是拿出一个元素。拿出之后就要循环排序好的部分,就是未排序好的元素的索引 -1 到数组0的部分。循环的时候,进行比较和移动元素。
public class SortArray { public static void insertSort(int[] a) { // 遍历数组,从未排序好的部分拿出每一个元素 for (int i = 1; i < a.length; i++) { // 拿出的未排序好元素 int unSortedElem = a[i]; // 排序好的部分最大索引就是未排序好元素的索引 - 1 int j = i - 1; // 从后向前遍历排序好的部分,找出未排序好的元素所在的位置 while (j >= 0 && unSortedElem < a[j]) { // 如果未排序好元素 小于 排序好的元素,排序好的元素后移,腾出位置 a[j + 1] = a[j]; // 同时继续向前遍历 j--; } // 未排序好的元素 大于 j 位置处元素。j+1 就是未排序好的元素所在的位置 a[j + 1] = unSortedElem; } } }
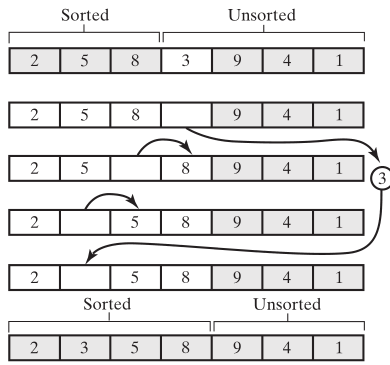
如要以递归的方式,实现插入排序,假设要排序7个数,如果前6个都排序好了,直接用最后一个和前面的数进行比较就好了,当排序第6个数的时候,如果前面5个排序好了,也是进行比较,可以看作是自己调用自己。假设声明一个方法 insertionSort(int[] a, int first, int last){}, 自己不停地调用自己。
public class SortArray { public static void insertionSort(int[] a, int first, int last) { if(first < last) { System.out.println(first +" " + last); insertionSort(a, first, last -1); } } public static void main(String[] args) { int[] arr = {8, 2, 6, 4, 9, 7, 1}; insertionSort(arr, 0, arr.length - 1); } }
最后first是0,last是1,last-1是0,所以数组索引first到last-1是排好序的,last是待排序的。所以要在if语句里面,insertingSort后面进行排序,就是先last和last-1进行比较,直到begin, 然后再比较和换位置。排序的函数为insertInOrder(int[] a, int unSortElement, int sortedArrBegin, int sortedArrEnd) {}, 调用的时候就是insertInOrder(a, a[last], first, last -1)。那insertInOrder里面怎么排序呢?unSortElement和数组a[sortedArrEnd]进行比较,如果是大于等于,直接把unSortElement放到sortedArrEnd+1位置。

如果小于,那就sortedArrEnd处的元素向后移动一下,unSortElement再和sortedArrEnd - 1处的元素进行比较,又是一轮insertInOrder,

最后有可能sortedArrEnd 一直向前移动,和begin相等于,unSortElement还是比sortedArrEnd 小,那就把sortedArrEnd 向右移一下,unSortElement直接赋值给sortedArrEnd ,也就是begin
public static void insertInOrder(int[] a, int unSortElement,int sortedArrBegin, int sortedArrEnd) { if (unSortElement >= a[sortedArrEnd]) a[sortedArrEnd + 1] = unSortElement; else if (sortedArrBegin < sortedArrEnd) { a[sortedArrEnd + 1] = a[sortedArrEnd]; insertInOrder(a, unSortElement, sortedArrBegin, sortedArrEnd - 1); } else // begin == end and anEntry < a[end] { a[sortedArrEnd + 1] = a[sortedArrEnd]; a[sortedArrEnd] = unSortElement; } }
整个算法如下
import java.util.Arrays; public class SortArray { public static void insertionSort(int[] a, int first, int last) { if (first < last) { insertionSort(a, first, last - 1); insertInOrder(a, a[last], first, last-1); } } public static void insertInOrder(int[] a, int unSortElement,int sortedArrBegin, int sortedArrEnd) { if (unSortElement >= a[sortedArrEnd]) a[sortedArrEnd + 1] = unSortElement; else if (sortedArrBegin < sortedArrEnd) { a[sortedArrEnd + 1] = a[sortedArrEnd]; insertInOrder(a, unSortElement, sortedArrBegin, sortedArrEnd - 1); } else // begin == end and anEntry < a[end] { a[sortedArrEnd + 1] = a[sortedArrEnd]; a[sortedArrEnd] = unSortElement; } } public static void main(String[] args) { int[] arr = {8, 2, 6, 4, 9, 7, 1}; insertionSort(arr, 0, arr.length - 1); System.out.println(Arrays.toString(arr)); } }
插入排序的方法,还可以对单链表进行排序。和数组一样,把链表分为两个部分,一部分是排序好的部分,一部分是未排序的部分。刚开始的时候,排序好的部分就只有链表的第一个元素,这时可以想像成两个链表。 循环未排序的部分,拿出每一个元素,然后向排序好的链表部分执行插入操作,链表的插入操作时,找到合适的位置,就相当于进行排序了。链表分为两个部分
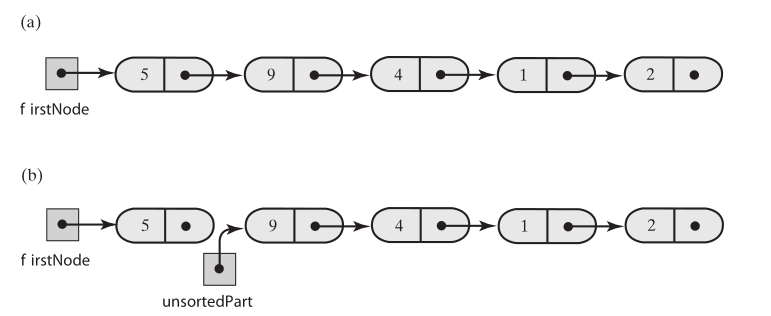
假设有一个链表
public class LinkedChain { private class Node { int data; Node next; Node(int data) { this.data = data; this.next = null; } } private Node firstNode; }
那么分成两部分的代码就是
Node unsortedPartHeader = firstNode.next; firstNode.next = null;
循环未排序的部分
while (unsortedPartHeader != null){ Node nodeToInsert = unsortedPartHeader; unsortedPartHeader = unsortedPartHeader.next;
insertInOrder(Node nodeToInsert); }
nodeToInsert 就是每一个要插入的元素,insertInOrder就是链表的插入算法
// 插入元素的方式 private void insertInOrder(Node nodeToInsert) { int data = nodeToInsert.data; Node current = firstNode; Node previous = null; // 按照排序找到合适的位置 while (current != null && current.data < data){ previous = current; current = current.next; } // 如果不是null,就表明插入的位置是中间位置 if(previous != null) { previous.next = nodeToInsert; nodeToInsert.next = current; } else { // 插入的位置是第一个位置 nodeToInsert.next = firstNode; firstNode = nodeToInsert; } }
创建几个Node测试一下
public class LinkedChain {
private class Node {
int data;
Node next;
Node(int data) {
this.data = data;
this.next = null;
}
}
private Node firstNode;
public void insertNode() {
//首先把链表分为两个部分,一个是排好序的,就是链表的第一个元素,一个是未排好序的.
Node unsortedPartHeader = firstNode.next;
firstNode.next = null;
// 循环未排序的部分,拿出每一个元素
while (unsortedPartHeader != null){
Node nodeToInsert = unsortedPartHeader;
unsortedPartHeader = unsortedPartHeader.next;
insertInOrder(nodeToInsert);
}
}
// 以插入元素的方式把
private void insertInOrder(Node nodeToInsert) {
int data = nodeToInsert.data;
Node current = firstNode;
Node previous = null;
// 按照排序找到合适的位置
while (current != null && current.data < data){
previous = current;
current = current.next;
}
// 如果不是null,就表明插入的位置是中间位置
if(previous != null) {
previous.next = nodeToInsert;
nodeToInsert.next = current;
} else { // 插入的位置是第一个位置
nodeToInsert.next = firstNode;
firstNode = nodeToInsert;
}
}
public void createNode() {
Node first = new Node(5);
Node second = new Node(9);
Node third = new Node(4);
Node fouth = new Node(1);
Node five = new Node(8);
first.next = second;
second.next = third;
third.next = fouth;
fouth.next = five;
firstNode = first;
}
public void display() {
Node current = firstNode;
while (current != null) {
System.out.print(current.data + " ");
current = current.next;
}
}
public static void main(String[] args) {
LinkedChain lc = new LinkedChain();
lc.createNode();
lc.insertNode();
lc.display();
}
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号