中缀表达式转后缀表达式

　　先看几个中缀表达式和它们对应的后缀表达式的例子，后缀表达式，是操作符在操作数的后面

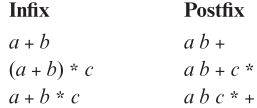
　　操作数a, b, c 在中缀表达式中的顺序和在后缀表达式中的顺序是一致的，但操作符的顺序可能要发生变化，因为在中缀表达式中操作符有优先级，括号也能改变运算的优先级，这些都要在后缀表达式中体现出来，后缀表达式中没有括号。那怎么转化呢？

　　1，创建一个变量，初始化为空的字符串，来表示要完成的后缀表达式，创建一个字符栈，用来存储操作符

　　2，从左向右依次扫描中缀表达式，

　　　　遇到操作数，直接加到后缀表达式的后面 ，因为，在中缀表达式和后缀表达式中，操作数的顺序是一样的，

　　　　遇到操作符，要先存起来，存到栈中，因为操作符有优先级，它要和后面的操作符比较优先级，然后才能决定把它放到什么哪个位置。

　　　　　　如果栈为空，直接把操作符放入栈中

　　　　　　如果栈不为空，比较优先级。

　　　　　　　　如果遇到的操作符比栈顶中的操作符优先级高，把遇到的操作符放入栈中。

　　　　　　　　如果遇到的操作符和栈顶操作符的优先级相等，这要考虑操作符的结合性，它是从左到右结合，还是从右到左结合。

　　　　　　　　　　从左到右接合，就是操作数属于它前面的操作符而不是它后面操作符。+, - , * , / 就是从左向右结合，比如a-b+c中的b是-的操作数，而不是+的操作数，整个表达式，也是从左向右计算的。

　　　　　　　　　　从右向左结合，操作数属于它前面的操作符而不是它后面操作符，比如阶乘。a ^ b ^ c， b是第二个^的操作数，而不是第一个^的操作数，整个表达式也是从右向左计算，a ^ (b ^ c)。

　　　　　　　　　　如果从左向右接合，那就弹栈，把操作符放到后缀表达式中，如果从右向左结合，则把遇到的操作符放入栈中(和优先级高的情况一致)

　　　　　　　　如果遇到的操作符比栈顶中的操作符优先级低，那就弹栈，把操作符放到后缀表达式中

　　　　遇到(，放到字符栈，因为要等到)才能知道怎么操作。

　　　　遇到)，依次从字栈中弹栈，放到后缀表达式中，直到遇到(,  遇到(, 要把它弹栈，然后舍弃掉。

　　3，循环完毕，如果字符栈中还有操作符，依次弹栈放到后缀表达式中，最终栈为空，得到完整的后缀表达式。

　　举几个例子，来理解一下转化过程，如果遇到的操作符比栈顶的操作符优先级高，比如把a + b * c。先创建空字符串作为后缀后达式，再从左到右扫描中缀表达式，把a放到新建后缀表达式后面，把+存到栈中，然后把b放到后缀表达式后面，这时遇到了*，*号的优先级比栈中的+高，也就是说，操作数b并不是+的第二个操作数，而是乘号的操作数，+的操作数要等待*的运算结果，这时把*放入到栈中，再把c放到后缀表达式中，中缀表达式扫描完毕，这时把操作符从栈中pop()出来，依次放到后缀表达式的后面，得到整个后缀表达式是abc*+

 

　　遇到的操作符和栈顶操作符的优先级相等，但是从左向右结合，比如a-b+c。创建空字符串表示后缀表达式，ab放到空字符中，-放入到字符栈中，此时遇到+，+和-的优先级相等，+的操作要等它左边表达式的结果，也就是说，要先算减的结果，a，b属于-，所以把-弹栈，放到后缀表达式中，此时栈为空，再把+放入到栈中。把c放到后缀表达式，弹栈+，把+放到表达式中。最终，a-b+c的后缀表达式为ab-c+

 　　遇到的操作符和栈顶操作符的优先级相等，但是从右向左结合，比如a ^ b ^ c, 创建空字符串表示后缀表达式，ab放到空字符中，^放入到字符栈中，此时又遇到^，它和栈顶中的^优先级相等，但^是从右向左接合，要先计算后边的结果，所以还是把^入栈，c放到后缀表达式，依次弹栈^，放到表达式中。最终，a ^ b ^ c的后缀表达式为a b c ^ ^

 

　　括号改变了操作符的优先级，总是把左括号放到栈上，然后也把它当作操作符，它的优先级是最低的，也就是说后续的操作符都会放到栈中。当遇到右括号，从堆栈中弹出运算符并将它们附加到形成的后缀表达式中，直到弹出一个左括号。

　　综上所述，中缀表达式转化为后缀表达式，步骤如下:

　　从左向右依次扫描中缀表达式，

　　　　如果遇到操作数，就放入到后缀表达式字符串中，默认是空字符串。

　　　　如果遇到^，就入字符栈。

　　　　如果遇到+, -, *, /,  如果栈不为空并且新来的操作符比栈项的操作符优先级低，就不停弹栈，添加到后缀表达式中，然后把新的操作符入栈。

　　　　如果遇到 (，入字符栈。

　　　　如果遇到 )，依次弹字符栈，添加到后缀表达式中，直到遇到(，然后把它舍弃掉。

　　扫描完毕后，如果字符栈不为空，再依次弹字符栈，添加到后缀表达式中。

import java.util.Stack;

public class InfixToPostfix {
    public static String convertToPostfix(String infixExpression){

        // 创建字符栈
        Stack<Character> operators = new Stack<>();

        // 创建将要实现的后缀表达式，初始为空
        StringBuilder postfix = new StringBuilder();

        for (int i = 0; i < infixExpression.length(); i++) {

            char c = infixExpression.charAt(i);

            // 如果中缀表达式中有空格
            if (c == ' ') {
                continue;
            } else if (c == '^'){
                operators.push(c);
            } else if (c == '+' || c == '-' || c == '*' || c == '/' ){
                while (!operators.isEmpty() && priority(c) <= priority(operators.peek())){
                    postfix.append(operators.pop());
                }

                operators.push(c);
            } else if (c == '('){
                operators.push(c);
            } else if(c == ')'){
                while (operators.peek() != '('){
                    postfix.append(operators.pop());
                }
                operators.pop();
            } else {
                postfix.append(c);
            }
        }

        while (!operators.isEmpty()){
            postfix.append(operators.pop());
        }

        return postfix.toString();

    }

    private static int priority(char operator) {
        if(operator == '*' || operator == '/' ) {
            return 1;
        } else if (operator == '+' || operator == '-' ) {
            return 0;
        } else {
            return -1;
        }
    }
}

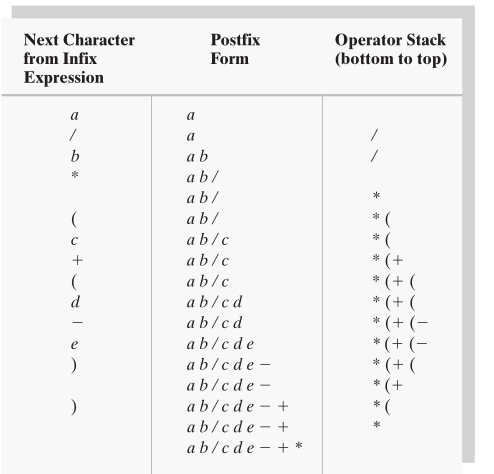
　　调用 convertToPostfix("a  / b  * (c  + (d  - e))")，得到后缀表达式为a b / c d e − + *。