递归

　　递归就是大问题能转化成小问题，小问题还能转成更小的问题，更小的问题还能继续转化成更更小的问题，一直持续转化，直到最后，出现了一个最最小的问题。一看这个问题，马上知道答案了。这时，最最小的问题解决了，更更小问题也就好解决了，更小的问题也就解决了，小问题也就解决了，最终整个问题得到解决。大问题和小问题，就是大小不同或解决的问题的规模不同，其它一模一样。

　　递归，体现到编程语言上，就是函数自己调用自己。大问题能转化成小问题，就是函数自己调用自己一次，调用的时候，把函数参数变小一点，问题规模就变小一次，小问题还能转成更小的问题，就是函数再调用自己一次，调用的时候，再把参数设小一点，规模变小了，直到最后，函数自己就能解决传递过来的参数了，问题规模自己能控制住了，就不用再调用自己了。每一个小问题都是一个函数，函数与函数之间，完全相同，只不过每一个函数解决的问题大小不同。举个例子

function countDown(n) {
    console.log(n);
    if (n > 1) {
        countDown(n - 1);
    }
}

countDown(3)

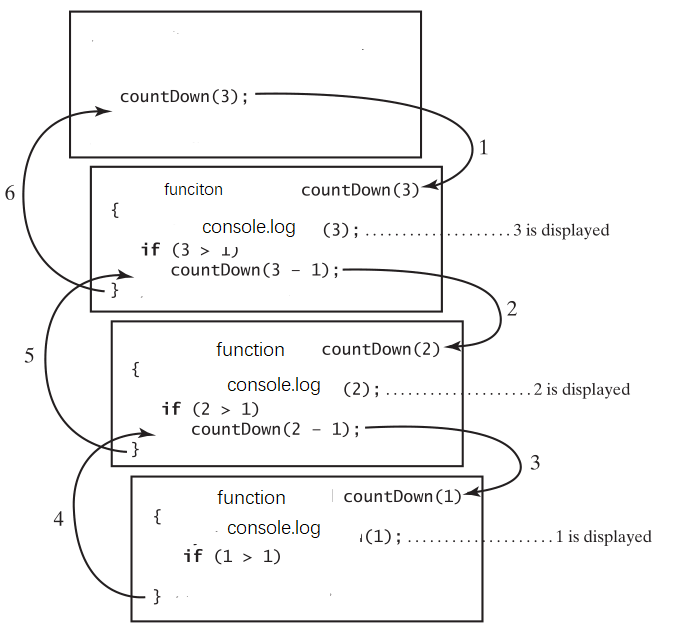
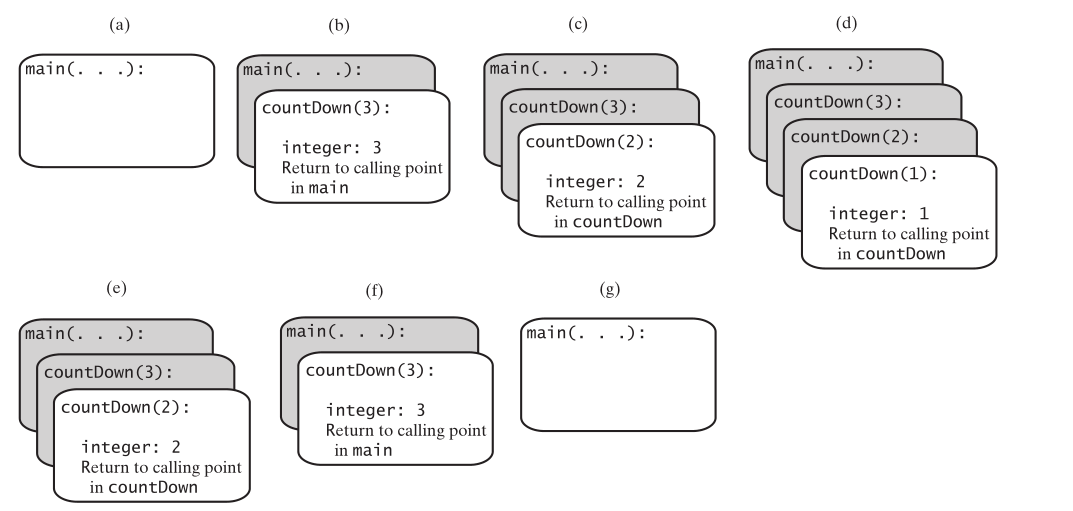
　　countDown(3); 正常的函数调用，把3赋值给了n，下列语句被执行

console.log(3);
if (3 > 1) {
    countDown(3 - 1);
}

　　countDown(3-1); 也就是countDown(2); 函数自己调用了一次自己，但参数由3变成了2，问题规模变小了，但countDown(3)函数也不会再向下执行了，它依赖countDown(2)函数的执行结果。countDown(2)执行导致下列语句执行。

console.log(2);
if (2 > 1) {
    countDown(2 - 1);
}

　　countDown(2 − 1); 也就是countDown(1)，函数自己又调用了一次自己，但参数由1变成了1，问题规模又小了，但countDown(2)函数也不会再向下执行了，它依赖countDown(1)函数的执行结果。countDown(1)，会如下执行

console.log(1);
if (1 > 1) {
    countDown(1 - 1);
}

　　if(1>1)没有成立，函数终于可以自己解决问题了，不用再调用别人了。countDown(1) 输出1，就执行结束了，countDown(2)依赖countDown(1)，countDown(1)执行结束了，返回到了countDown(2)，countDown(2) 也执行结束了。countDown(2) 返回countDown(3) , countDown(3) 也就执行结束了，整个函数调用结束。

 　　再举一个例子

function upAndDown(n) {
    console.log("before call " + n);
    if (n < 3) {
        upAndDown(n + 1);
    }
    console.log("after call " + n);
}

upAndDown(1)

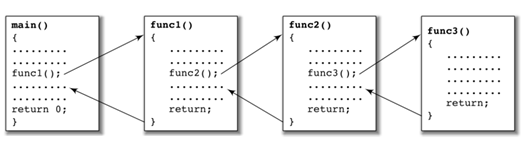
　　程序执行时，调用upAndDown(1)， 函数接受到参数1，开始执行， 输出了 "before call 1",  if 判断(1< 3)成立，函数调用自己，upAndDown(2)把参数2传递过来，函数upAndDown开始执行，函数执行永远都是从函数第一行语句开始执行，它输出了"before call 2"。 这里要注意的是函数upAndDown(1)并没有执行完， 它还等着upAndDown(2)的返回，并执行后面的console.log语句，所以n =1 是会保存起来的。函数upAndDown(2) 继续执行，还是if 判断(2 < 3) 成立，继续调用自己，生成了一次函数的调用upAndDown(3)，并把参数3，传递过去，此时，upAndDown(2)也没有执行完成，它在等待upAndDown(3) 的执行结果。upAndDown接受到参数3，开始执行，输出"before call 3"，进行if 判断，由于3 < 3 不成立，if代码块不会执行，函数终于不用再继续调用自己了，同时，函数也有机会执行到if 后面的语句了，输出"after call 3"， 由于console.log() 后面没有语句了，函数执行完毕，upAndDown(3) 调用完了，它会返回到调用它的upAndDown(2) 函数，upAndDown(2) 终于有机会执行了，它会继续执行函数调用语句后面的语句，也就是console.log("after call " + n), 由于upAndDown(2) 的空间中保存着n的信息，那就是2， 所以输出了"after call 2"。 upAndDown(2)执行完，返回到upAndDown(1)，upAndDown(1) 同样是输出 "after call 1" ,  然后返回，主程序中upAndDown(1) 后面并没有执行语句，所以整个程序结束。再画一张图

　　函数纵然是自己调用自己，但每一次的调用都是一个全新的函数， 栈中为这个函数调用开辟的空间中保存着这个函数调用的完整信息，这个函数没有执行完之前，这些信息永远都会存在，也就是函数返回时，它依然能够获取调用时的信息。　　

　　如果一个函数递归调用了(自己调用了自己)5次，可以把它想成5个函数的调用，fn1 调用fn2(), fn2调用fn3(), fn3调用了fn4(), fn4调用了fn5(), 只不过fn1, fn2, fn3, fn4, fn5 都是一样的函数。函数的每一次调用，都会栈中开辟一块空间，保存着这个函数调用的所有信息，比如传递过来的参数，如果该函数没有执行完，这些信息是不会释放的。fn1调用fn2() , 如果fn2()没有完成，并返回到fn1，fn1的空间永远都不会释放，它里面的保存的信息会一直存在。同理，fn2 调用了fn3(), 如果fn3没有执行完，fn2的空间也就不会释放。 正是由于函数不停地调用，不停地分配内存空间，总有一个函数要返回，不会再调用函数，否则内存就使用完了。对于递归来说，就是函数不会再调用自己了，这也就是说，递归函数的内部肯定存在一个条件，当达到这个条件的时候，函数不会调用函数(自己)。函数的返回是返回到调用它的函数的地方，fn5执行完了，永远都是返回到fn4, fn4在执行的时候，是从调用fn5() 的地方开始向下继续执行,  相当于在 fn4中，调用函数结束了，开始执行调用函数语句下面的语句。当一个函数调用另一个函数的时候，被调用的函数永远都是从函数第一行语句开始执行。

 　　countDown函数的调用

 

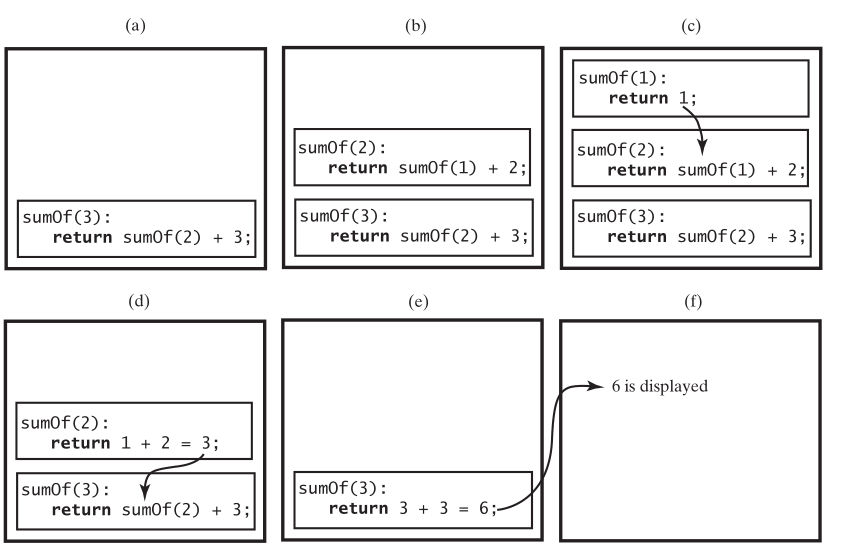
 　　有返回值的函数递归，就是每一次的函数自己调用自己都要有返回值。假设计算1到n的和

function sumOf(n) {
    if (n == 1)
        return 1;
    else
        return sumOf(n - 1) + n; // 递归调用
}

　　sumOf(3) 调用函数，return sumOf(3 - 1) + 3; sumOf(3) 延迟执行，等待sumOf(2)的执行结果。

　　sumOf(2) 调用函数，return sumOf(2 - 1) + 2; sumOf(2) 延迟执行，等待sumOf(1)的执行结果。

　　sumOf(1) return 1; 执行结束，返回到sumOf(2),

　　sumOf(2) return sumOf(1) +2， return 1+2， return 3，结束返回到sumOf(3)

　　sumOf(3) return sumOf(2) +3，就是return 3 + 3，就是6。整个函数执行结束。

　　有的时候，问题的解决是通过调用递归函数解决的，这时，调归函数也称为递归辅助函数(Recursive Helper Methods)。比如判断回文数

public class RecursivePalindrome {
    public static boolean isPalindrome(String s) {
        return isPalindrome(s, 0, s.length() - 1);
    }

    private static boolean isPalindrome(String s, int low, int high) {
        if (high <= low) // Base case
            return true;
        else if (s.charAt(low) != s.charAt(high)) // Base case
            return false;
        else
            return isPalindrome(s, low + 1, high - 1);
    }
}

　　第一个方法isPalindrome(String s) 判断字符串是不是回文数，第二个方法isPalindrome(String s, int low, int high) 判断子串(low... high) 是不是回文数。第一个方法传参字符串s，low=0，high=s.length-1给第二个方法，第二个方法，递归的调用自己来判断不断缩小的字符串是不是回文数。在递归编程中，定义接收更多参数的第二个方法是一种常见的编程模式。这个方法也叫递归辅助函数。

　　尾递归

　　递归函数的最后一条执行语句是函数的递归调用，没有额外的操作附加在递归调用上。

function countDown(n) {
    if (n >= 1) {
        System.out.println(n);
        countDown(n - 1); // 最后一句是调用函数
    }
} 

 　　求阶乘，如果不是尾递归

if (n < 0)
return 0;
else if (n == 0)
return 1;
else if (n == 1)
return 1;
else
return n * fact(n - 1);

　　函数的执行过程，有两个阶段，

 　　A recursive function is said to be tail recursive if all recursive calls within it are tail
recursive. A recursive call is tail recursive when it is the last statement that will be
executed within the body of a function and its return value is not a part of an
expression. Tail-recursive functions are characterized as having nothing to do dur-
ing the unwinding phase.

When a compiler detects a call that is tail recursive, it overwrites the current acti-
vation record instead of pushing a new one onto the stack. The compiler can do
this because the recursive call is the last statement to be executed in the current
activation; thus, there is nothing left to do in the activation when the call returns.
Consequently, there is no reason to keep the current activation around. By replac-
ing the current activation record instead of stacking another one on top of it, stack
usage is greatly reduced, which leads to better performance in practice. Thus, we
should make recursive functions tail recursive whenever we can.

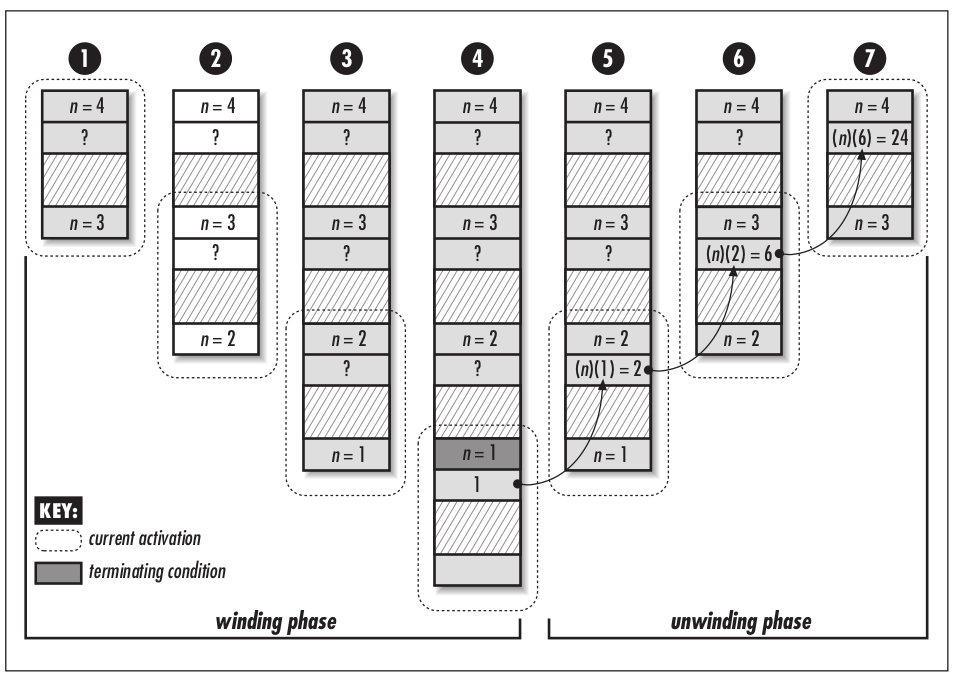
　　计算4的阶乘

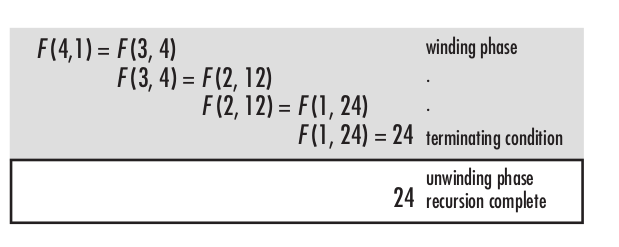
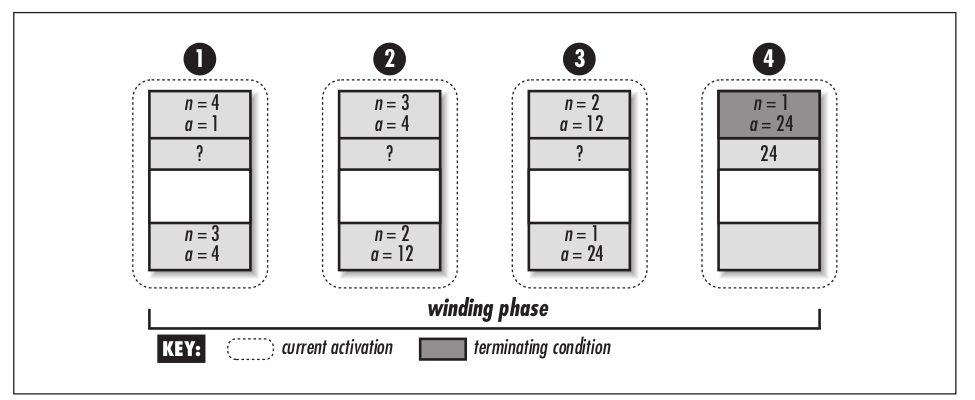
　　实现方式

int facttail(int n, int a) {
    if (n < 0)
        return 0;
    else if (n == 0)
        return 1;
    else if (n == 1)
        return a;
    else
        return facttail(n - 1, n * a);
}

　　执行过程