归并排序求逆序对

归并排序求逆序对

逆序对：对于数列的第 \(i\) 个和第 \(j\) 个元素，如果满足 \(i < j\) 且 \(a[i] > a[j]\)，则其为一个逆序对。

暴力求法就是两遍for循环，\(O(n^2)\)超时

用归并可以顺便求出来，\(O(nlogn)\)

在一次归并排序中，因为归并要求将一个完整区间分为两块，所以逆序对出现了三种情况。

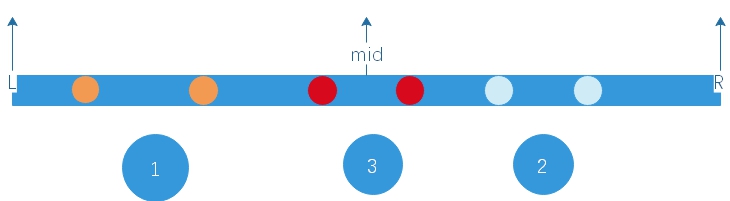
1. 逆序对在mid的左边
2. 逆序对在mid的右边
3. 逆序对的两个元素一个在mid左边，一个在mid右边

之前提过归并可以顺便求出来，这里设归并排序有大小为该区间逆序对个数的返回值，即\(l-r的逆序对个数=merge\_sort(l,r)\)

因为是递归处理嘛，所以先将左右两边的归并排序。重点是第三部分，如何处理这种情况。

首先，通过前两次归并排序，从\(L-mid，mid+1-R\)两个部分都是有序的，在合并这两个有序序列时，可以求出第三种情况的逆序对个数。

重新想一下逆序对的定义，是在前面的数比后面的数大。在区间上来看，就是\(L-mid\)的这一部分中有元素比\(mid+1-R\)中的元素大。

每次移动右半边的指针时，从中间到左半边指针所包含的所有数字 都是大于右半边指针所指向的数字的，这些都可以组成逆序对，直接加上即可。

最后呢，其实1和2的情况没有讨论，因为归并排序最后还是要分到只有两个数进行排序的。一个数不能构成逆序对，所以只有两个数字的情况下，只存在第三种情况，接着往下递归就不需要考虑12了。

代码：

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
const int maxn = 1e5 + 10;
int n, q[maxn], tmp[maxn];

ll solve(int l, int r)
{
    if (l >= r)
        return 0;
    int mid = l + r >> 1;
    ll ans = solve(l, mid) + solve(mid + 1, r);
    int i = l, j = mid + 1, k = l;
    while (i <= mid && j <= r) {
        if (q[i] <= q[j])//特别要注意这个，虽然加不加等号对于排序而言并没有影响，但是求逆序数时，加不加等于号是两种情况。只有在严格大于的时候才是逆序数。
            tmp[k++] = q[i++];
        else {
            tmp[k++] = q[j++];
            ans += (mid - i + 1);
        }
    }
    while (i <= mid)
        tmp[k++] = q[i++];
    while (j <= r)
        tmp[k++] = q[j++];
    for (int i = l; i <= r; i++)
        q[i] = tmp[i];
    return ans;
}

int main()
{
    scanf("%d", &n);
    for (int i = 0; i < n; ++i)
        scanf("%d", &q[i]);
    ll res = solve(0, n - 1);
    cout << res;
}