学习记录:线段树
线段树 V1.0
之所以叫v1.0呢,是因为这是我第一次学这个数据结构。
考虑到重要性,以后在做题的过程中会对这篇博客做更新的。
概念
线段树是一种二叉搜索树,用于处理区间问题的数据结构。
与ST表不同的是,线段树支持点,区间修改。相应的,虽然预处理速度与ST表相同,都是\(O(logn)\),但查询速度比起ST表的\(O(1)\)要慢,是\(O(logn)\)。
线段树是建立在区间二分这个概念上的,树上的每个节点都代表了一段区间。
如图
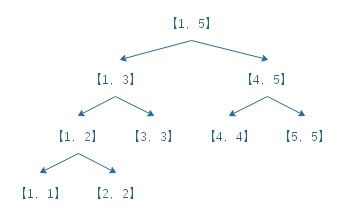
- 对于每个区间\([L,R]\)而言,都有一个左端点\(L\)和右端点\(R\)。
- 当\(L=R\)时,当前所指区间是一个点。显然,一个点是不能继续拆分的,所以这是一个叶子节点。
反过来考虑,\(L\neq R\)时,这一段区间必定包括了两个或以上的点,因此必有两个叶节点。
综上,线段树是没有只有一个子节点的节点的。 - 当\(L\neq R\)时,区间必然可以拆分为两个小区间。这里先设\(M=(L+R)/2\)。
左子节点的范围是\([L,M]\),相应的,右子节点的范围是\([M+1,R]\)。
对于二叉树这种结构,一般都用的是递归的方式。用指针难免会比较难处理,所以可以用完全二叉树的数组储存的方式,将线段树存放到数组里。
对于上图的线段树,用数组储存后的表现是
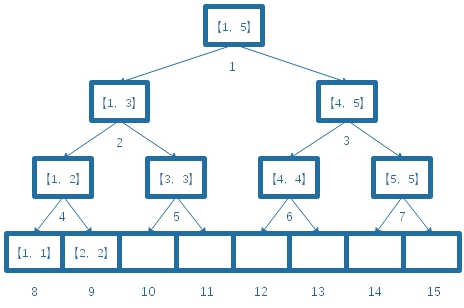
这样储存,大概率会需要比较多的空间。一般来说,有n个点时需要4n的空间(\(2\times 2^k(2^{k-1}<n<2^k)\))
如果学过完全二叉树,那么父子节点的关系就很清楚。设父节点下标为K,则有
- L=K*2(左节点)
- R=K*2+1(右节点)
因为父子节点的关系有2倍关系,经常会用位运算的方式来计算下标,如
- L=K<<1(向左移一位,相当于*2)
- R=k<<1|1 (向左移一位,再加上1,相当于*2+1)
代码实现
创建线段树
既然是一种二叉树的结构,一般用递归来做会比较简单。
const int maxn = 1e2 + 10;
int a[maxn] = {0, 1, 2, 3, 4, 5, 6, 7};//原数组
int tree[maxn * 4];//需要建树的
void print(int n)//输出tree的函数,这个自己随便写写,方便看就行
{
for (int i = 1; i < n * 4; i++)
{
if ((i & (i - 1)) == 0)
cout << endl;
cout << setw(4) << tree[i];
}
}
void Pushup(int k)//更新函数 k:线段树节点下标
{
tree[k] = max(tree[k * 2], tree[k * 2 + 1]);//这里以最大值为例,这句话视题目意思而定
}
void Build(int l, int r, int k)//建树函数 l:原数组a的左端点 r:原数组a的右端点 k:当前线段树节点下标
{
//比如该例中a要建树的范围是1~7,那么l=1,r=7
//k默认选1.不要选0!0*2=0,失去了找子节点的功能
//一开始建树的时候,k指的就是根节点所在下标
if (l == r)//左右端点相等,说明现在是一个点,直接把原数组的东西复制过来
tree[k] = a[l];
else//否则就肯定是一段区间
{
int m = (l + r) / 2;//确定中点
Build(l, m, k * 2);//递归建左子树
Build(m + 1, r, k * 2 + 1);//递归建右子树
//这两句位置变动没有影响,不过要注意范围和k的值
Pushup(k);//更新当前节点
}
}
int main()
{
Build(1, 7, 1);//a数组下标1~7的建树,tree数组从1开始
print(7);
return 0;
}
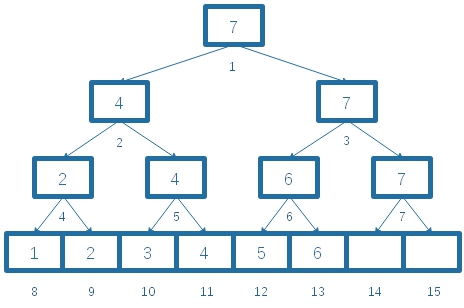
结果如图:
PS:7下面是空的
点更新
点更新很易于理解。从需要更改的根节点出发,将每一个覆盖到这个点的区间都更新一次即可。
void updata(int p,int val,int l,int r,int k)//p:需要更改的原数组下标 val:增加的值 l:原数组的左端点 r:原数组的右端点 k:
{
if (l==r)//说明是单点,加上就好了
a[p] += val, tree[k] += val;//原数组和线段树数组都加
else{
int m = (l + r) / 2;//中点
if (p<=m){//要修改的点在左子树上,记得有等于号!
updata(p, val, l, m, k * 2);
}else{//在右子树上
updata(p, val, m + 1, r, k * 2 + 1);
}
Pushup(k);//更新当前节点
}
}
区间查询
也很容易理解:查询的是一段区间,我们只需要将这个区间所包含的子区间——也就是在预处理中已经算好的值都拿出来就行
代码如下:
int Query(int L, int R, int l, int r, int k)//L,R:要查询的区间范围 l,r:当前的区间范围 k:当前线段树下标
{
if (L <= l && r <= R)//当前区间完全包含在查询区间内,直接返回
return tree[k];
else
{
//可能包括了左端点,也可能有右端点
int res = 0;//答案,注意初始化的值要随题目意思改变
int m = (l + r) / 2;//中点
if (L <= m)//左子树与查询区间有交集
res = max(res, Query(L, R, l, m, k * 2));//这句话应题目意思而变,该例中是最大值
if (R >= m+1)//右子树与查询区间有交集,注意右区间从m+1开始
res = max(res, Query(L, R, m + 1, r, k * 2 + 1));
return res;//返回答案
}
}
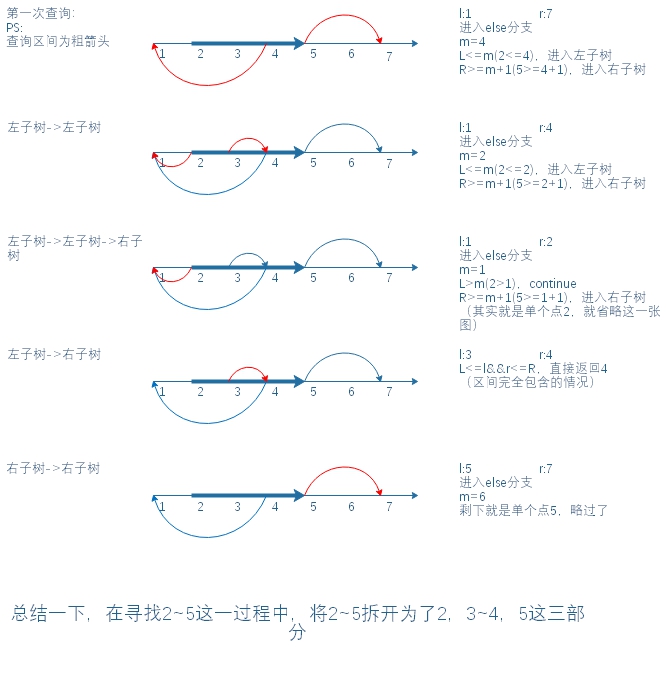
其实查询比上面两种操作还是要难,配合图片更容易理解
这里假设要查询2~5之间的最大值
区间修改
大意:指定\(i,j \leq n\),将区间\([a,b]\)的每个数字加c
直接套用点修改的方式在时间复杂度上并不比直接在数组上修改好,此时要用一种“懒惰”的做法
lazy-tag:修改整个区间时,只对这个区间进行整体性的修改,内部的每个元素则暂时不做处理。只有当这个线段区间的一致性被破坏时,才对子区间的值做修改。
模板
/*
简写说明:
cur:当前线段树下标
l,r:要进行处理的区间
seg:线段树数组名
lazy:懒惰标记
*/
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
const int maxn = 1e5 + 10;
ll num[maxn], seg[maxn << 2], lazy[maxn << 2];
void print(int n) //输出tree的函数,这个自己随便写写,方便看就行
{
for (int i = 1; i < n * 4; i++)
{
if ((i & (i - 1)) == 0)
cout << endl;
cout << setw(4) << seg[i];
}
cout << endl;
for (int i = 1; i < n * 4; i++)
{
if ((i & (i - 1)) == 0)
cout << endl;
cout << setw(4) << lazy[i];
}
cout << endl;
}
void Pushup(int cur)//向上更新函数,这里是求区间和
{
seg[cur] = seg[cur << 1] + seg[cur << 1 | 1];
}
void Pushdown(int cur, int l, int r)
{
if (lazy[cur])
{
int m = (l + r) >> 1;
lazy[cur << 1] += lazy[cur];
lazy[cur << 1 | 1] += lazy[cur];
seg[cur << 1] += lazy[cur] * (m - l + 1);
seg[cur << 1 | 1] += lazy[cur] * (r - m);
lazy[cur] = 0;
}
}
void Build(int cur, int l, int r)
{
if (l == r)
seg[cur] = num[l];
else
{
int m = (l + r) >> 1;
Build(cur << 1, l, m);
Build(cur << 1 | 1, m + 1, r);
Pushup(cur);
}
}
void Point(int index, int val, int l, int r, int cur)
{
if (l == r)
num[index] += val, seg[cur] += val;
else
{
int m = (l + r) >> 1;
if (index <= m)
Point(index, val, l, m, cur << 1);
else
Point(index, val, m + 1, r, cur << 1 | 1);
Pushup(cur);
}
}
void updata(int L, int R, int val, int l, int r, int cur)
{
if (L <= l && r <= R)
{
lazy[cur] += val;
seg[cur] += val * (r - l + 1);
}
else
{
Pushdown(cur, l, r);
int m = (l + r) >> 1;
if (L <= m)
updata(L, R, val, l, m, cur << 1);
if (m < R)
updata(L, R, val, m + 1, r, cur << 1 | 1);
Pushup(cur);
}
}
ll Query(int L, int R, int l, int r, int cur)
{
if (L <= l && r <= R)
return seg[cur];
else
{
Pushdown(cur, l, r);
ll res = 0;
int m = (l + r) >> 1;
if (L <= m)
res += Query(L, R, l, m, cur << 1);
if (R >= m + 1)
res += Query(L, R, m + 1, r, cur << 1 | 1);
return res;
}
}
int main()
{
int n, m;
cin >> n >> m;
for (int i = 1; i <= n; i++)
cin >> num[i];
Build(1, 1, n);
int flag, x, y, k;
while (m--)
{
cin >> flag;
if (flag == 1)
{
cin >> x >> y >> k;
updata(x, y, k, 1, n, 1);
}
else
{
cin >> x >> y;
cout << Query(x, y, 1, n, 1) << endl;
}
}
return 0;
}


