学习记录：ST表

ST表简介

ST 表是用于解决 可重复贡献问题 的数据结构

可重复贡献问题：是指对于运算\(opt\)，满足\(x\ opt\ x =x\)，则对应的区间询问就是一个可重复贡献问题。（摘自OI wiki）

说人话，就是对区间的重复运算不影响结果。比如区间最值问题（RMQ），区间GCD

比方10个数求最大值，先对前7个数求最值，再对后6个数求最值，中间有一段重复没有关系，最后再对求出的两个最值再求一次最值，这种方法是正确的。
按照第一段的话说，就是

\[max(1,2,...,10)=max(\ max(1,2,...,7)\ ,\ max(4,5,...,10)\ ) \]

ST表主要运用了倍增的思想，可以做到\(O(nlog_2n)\)预处理，\(O(1)\)回答每次询问，但不支持修改操作

具体实现

预处理

首先，令\(f(i,j)\)表示区间\([i,i+2^j-1]\)的最值

显然，\(f(i,0)\)表示区间\([i,i+2^0-1]\)，也就是\(a_i\)的值

在其他维度中，\(f(i,j)\)表示区间\([i,i+2^j-1]\)的最值，相比起\(f(i,j-1)\)而言，所表示的区间范围扩大了两倍。最开始提到过，对一个区间求最值的问题可以转换为对两个小区间分别求最值，既然是两倍范围，那么就可以拆成两个区间，这样就可以通过上一维度的信息求出当前维度的信息。

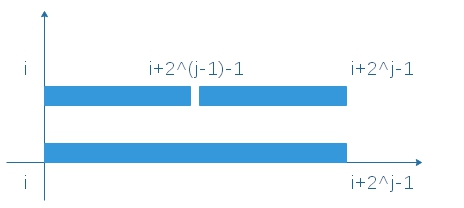
即\(f(i,j)=max(f(i,j-1),f(i+2^{j-1},j-1))\)

那么预处理的代码不难写出

void pre()
{
	for (int i=1;i<=n;i++)	//第一维的数据输入 
		cin>>f[i][0];
		
	for (int j=1;j<=21;j++)	//2^21大概是
		for (int i=1;i+(1<<j)-1<=n;i++)
			f[i][j]=max(f[i][j-1],f[i+(1<<j-1)][j-1]);//"<<"是左移运算，1<<x就是2^x
}

计算

预处理中，每一层维度的覆盖范围都是\(2^x\)，当然 每次询问的范围 都不可能刚好是这样的指数范围，因此，还要对运算的区间进行处理

根据可重复贡献问题的定义，重复区间的计算并不会对最值产生影响，那么就可以将待求区间划分为两个子区间

我们希望\(l+2^x-1=r\)，解得维度\(x\)应当为\(log_2(r-l+1)\)，显然\(x\)不一定是个整数，因此要进行取整操作
向上取整显然不行，因为引入了新区间
因此只能向下取整，当然覆盖范围会变小。解决方法便是再引入一个相同长度，但出发点不同的区间，他们的并集会覆盖整个所求区域。

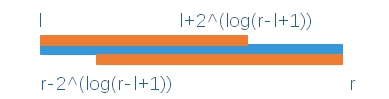
如图，第一个区间是向下取整，出发点依旧是\(l\)的区间，覆盖范围是\([l,l+2^{log_2(r-l+1)}-1]\)，也就是\(f(l,[x])\)
第二个区间向前移动了\(r-2^{[x]}\)，即\(f(r-2^{[x]}+1,[x])\)

最多只需要两个区间，便能求出任意区间上的最值，因此查询效率\(O(1)\)

代码如下：

void read()
{
    int l,r;
    cin>>l>>r;
    int lg=logn[r-l+1];	//logn是提前写好的向下取整的log数值
    int ans=max(f[l][lg],f[r-(1<<lg)+1][lg]);
    printf("%d\n",ans);
}

最后附一道模板题，【模板】ST表

#include <bits/stdc++.h>

using namespace std;
const int maxn = 1e5+10;
const int mod  = 100003;

int f[maxn][21];
int logn[maxn],n,m;
void pre()
{
	logn[1]=0,logn[2]=1;
	for (int i=3;i<=n;i++)
		logn[i]=logn[i/2]+1;
}
inline int read()
{
	int x=0,f=1;char ch=getchar();
	while (!isdigit(ch)){if (ch=='-') f=-1;ch=getchar();}
	while (isdigit(ch)){x=x*10+ch-48;ch=getchar();}
	return x*f;
}
int main()
{
	n=read(),m=read();//先读取了n才知道预处理的范围！
	pre();
	for (int i=1;i<=n;i++)
		f[i][0]=read();
	for (int j=1;j<=21;j++)
		for (int i=1;i+(1<<j)-1<=n;i++)
			f[i][j]=max(f[i][j-1],f[i+(1<<(j-1))][j-1]);
	while (m--)
	{
		int l=read(),r=read();
		int lg=logn[r-l+1];
		int ans=max(f[l][lg],f[r-(1<<lg)+1][lg]);
		printf("%d\n",ans);
	}
	return 0;
}