学习记录:哈夫曼树
哈夫曼树
基本概念
-
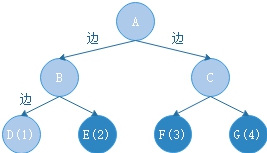
路径:在一棵树中, 从一个节点到另一个节点经过的所有结点,称为两个节点的路径。(图中淡蓝色为路径)
-
路径长度:从出发节点到目标节点,每经过一个节点,路径长度+1。可以理解为两个节点中间的边的数量。(标记为边的数量)
-
节点的权:每一个节点的权重。这个权重表示了这个节点的某种特性。(字母旁的数字)
-
带权路径长度:表示从根节点到该节点的路径长度与该节点的权的乘积。(例:\(D=2*1=2\))
-
树的带权路径长度:一个树上所有叶节点带权路径长度的和(\(Sum=2*1+2*2+2*3+2*4=20\))
哈夫曼树的定义
哈夫曼树就是在给定叶节点的情况下,树的带权路径长度最小的树。也被称为“最优二叉树”。
构建过程
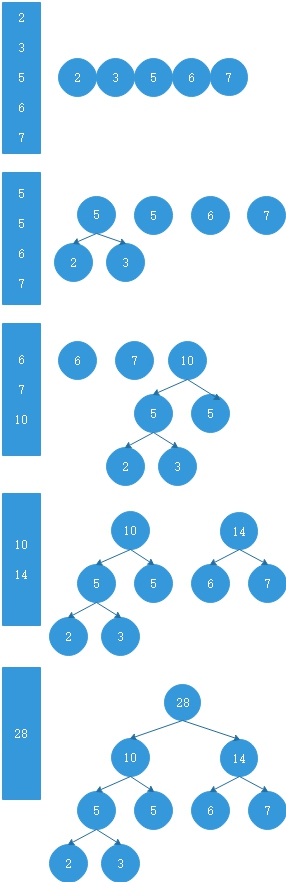
这里设要进行建树的数字为\(int\ num[]=\{2,3,5,6,7\};\)
- 将要建树的数字构建为优先队列,方便数据的处理。
- 取出优先队列的前两个数,将其组合为一个子树。
- 重复2直到队列中仅剩一个数,这时构建完成。
代码实现


 浙公网安备 33010602011771号
浙公网安备 33010602011771号