堆排序简介
堆排序
堆排序在我看来是一个比较难的排序算法,专门记录一下吧。
首先,先简单介绍一下堆这种结构。
堆排序,顾名思义,是利用堆这一数据结构进行的。堆是一种特殊的二叉树,其中每个元素都符合一定的规则。
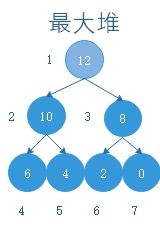
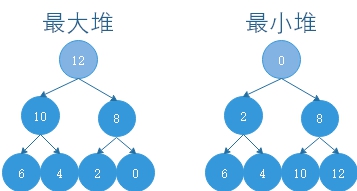
最大堆:每一个父节点,都比两个子节点大。最小堆就是父节点比子节点小。
当然数组是是一段顺序表,并不是这样的结构,现在以最大堆为例,将图上每一个点编上号。序号为从上到下,从左到右。
不难看出最大堆的一种性质:每个节点的下标乘2,乘2+1所获得的下标就是该节点的两个子节点的下标
这时就可以把最大堆的性质用数学形式表现出来了。对于最大堆的每一个节点,都有\(arr[i]>=arr[i*2]\&\&arr[i]>=arr[i*2+1]\)
从现在开始模拟一下堆排序的运行原理,其中还需要一些其他的函数,下面再说。
现在有一组元素已经按最大堆的方式排列就绪,从最后一个节点进行循环,直到只剩一个未经排序的节点为止。
对于每一个节点,将在堆顶的元素与当前节点交换。因为堆顶的元素是这个堆最大的元素,所以我们就找到了最大值的位置,并将它的值排在未经排序的序列的最后一个位置,也就是说排好了一个数据。
但是,经过交换后的堆,已经不满足最大堆的条件了,我们再用一个函数Adjust_Heap来将其重新恢复到最大堆的状态。接下来一直运行到循环结束为止。其实堆排序的主函数还是挺好写的。
void HeapSort(int *arr,int length)
{
for (int i=length-1;i>1;i--)
{
swap(arr[i],arr[1]);
HeapAdjust(arr,1,i-1);
}
/*for (int i=0;i<length;i++)//前移后面有解释
arr[i]=arr[i+1];*/
}
不过有两个问题。
- 怎么实现Adjust_Heap?
- 怎么把一个不满足最大堆的数组转换为最大堆?
第二个问题是依靠第一个问题的Adjust_Heap函数来实现的,先来看Adjust_Heap的工作原理。
Adjust_Heap如上文所述,是用来恢复最大堆的。再具体一点,这个函数需要知道当前不符合最大堆元素的位置,进行恢复的数据的范围。(后者很显而易见,不能把已经排好序的数字当作未排序的又放回原来位置吧)
这个函数的运行机制就是从给定的父节点开始,从两个子节点中选取最大的一个,并比较父节点与较大的子节点,如果父节点是最大的,说明已经处理完毕;否则交换这两个节点,继续向下比较。
void HeapAdjust(int *arr,int top,int range)//arr为数组首地址,top为需要进行恢复的元素下标,range就是范围啦
{
for (int i=top*2;i<=range;i*=2)//为什么是*2?因为要获得子节点的下标
{
if (i<range&&arr[i]<arr[i+1])
i++;//找到两个子节点中最大的元素的下标
if (arr[top]>=arr[i])
break;//不需要交换就退出
swap(arr[top],arr[i]);//父子节点交换
top=i;//现在要处理的点就是子节点
}
}
剩下的问题就只有一个了,如何将一个一般数组变换为最大堆的结构?这里我们用Initialize_Heap函数来实现。实现方式也很简单粗暴,对一半的数据都Adjust一遍就行了。
当然还是要解释一遍要对一半的数据进行调整。上面说过一个数据的下标*2就可以得到其子节点的下标,反过来说,只有这个数据的下标*2小于等于总数据个数的时候才会有子节点因此从有子节点的遍历处理一遍就好了当然全部过一遍也没什么问题。
void InitHeap (int *arr,int length)
{
/*for (int i=length;i>=1;i--)
arr[i]=arr[i-1];//数组是从0开始的,后移一次方便处理。别忘了最后换回来*/
for (int i=length/2;i>0;i--)
HeapAdjust(arr,i,length);//暴力过一遍
}
堆排序就写完啦~