【luogu P5320】勘破神机(数学)(数列特征方程)(第一类斯特林数)
勘破神机
题目链接:luogu P5320
题目大意
给你 \(l,r,k\)(其中 \(l,r\) 很大,\(k\leq 501\)),求:
\(\dfrac{1}{r-l+1}\sum\limits_{i=l}^rC_{f_i}^k\)
\(\dfrac{1}{r-l+1}\sum\limits_{i=l}^rC_{g_i}^k\)
\(f_n\) 为一个 \(2*n\) 的网格往里面放 \(1*2\) 的块填满的方案,\(g_n\) 则是一个 \(3*n\) 的网格。
思路
首先 \(2\) 的答案我们可以看出答案其实是贴合与斐波那契数列 \(F_i\)。
具体看一看会发现是 \(f_i=F_{i+1}\),所以记得 \(l,r\) 加一。
然后斐波那契嘛,\(f_i=f_{i-1}+f_{i-2}\),然后可以表示成那个带根号的通式嘛。
然后我们通过特征方程这个东西,我们知道如果有一个二阶递推式,我们可以把它表示成一个通项公式。
于是开始了下面的步骤:
2
\(f_i=f_{i-1}+f_{i-2}\)
\(f[n]=\dfrac{\sqrt{5}}{5}[(\dfrac{1+\sqrt{5}}{2})^n-(\dfrac{1-\sqrt{5}}{2})^n]\)
\(A=\dfrac{\sqrt{5}}{5},\alpha=\dfrac{1+\sqrt{5}}{2},B=-\dfrac{\sqrt{5}}{5},\beta=\dfrac{1-\sqrt{5}}{2}\)
3
思考要如何推出 \(f\) 的值,首先把 \(f_0,f_1\) 求出,因为可以作为边界,而且也是特征方程需要的。
\(f_0=1,f_1=3\)
\(f_i\) 长度为 \(2i\) 的答案(所以记得两个边界要改,但是注意 \(r-l+1\) 要用之前的值)
于是进行思考,发现可以新放进来一个 \(2*3\) 的,然后有 \(3\) 中方法。
然后发现只有这样不够,因为可能会出现这样的:
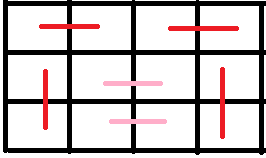
而且呢,中间的粉色可能不止两个:
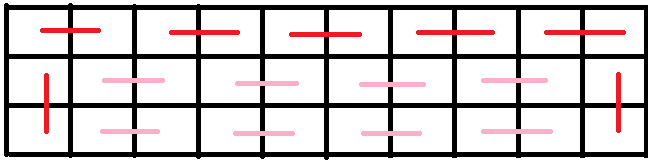
然后粉色可以是在 \(1,2\) 行或者 \(2,3\) 行,所以我们可以列出这样的式子:
\(f_{i}=3f_{i-1}+2(f_{i-2}+f_{i-3}+...)\)
\(f_i=3f_{i-1}+2(\sum\limits_{j=0}^{i-2}f_j)\)
\(f_{i-1}=3f_{i-2}+2(\sum\limits_{j=0}^{i-3}f_j)\)
\(f_i-f_{i-1}=3f_{i-1}-f_{i-2}\)
\(f_i=4f_{i-1}-f_{i-2}\)
搞出了二阶递推式,就直接开始求通项公式吧!
\(f_i-4f_{i-1}+f_{i-2}=0\)
\(x^2-4x+1=0\)
\(x_1=\dfrac{4+2\sqrt{3}}{2},x_2=\dfrac{4-2\sqrt{3}}{2}\)
\(x_1=2+\sqrt{3},x_2=2-\sqrt{3}\)
带入 \(f_0=1,f_1=3\)
\(Ax_1^n+Bx_2^n=f_n\)
\(A+B=1\)
\(A(2+\sqrt{3})+B(2-\sqrt{3})=3\)
\(A(2+\sqrt3)+(1-A)(2-\sqrt3)=3\)
\(A(2+\sqrt3)+2-\sqrt{3}-A(2-\sqrt3)=3\)
\(2\sqrt3A=1+\sqrt3\)
\(A=\dfrac{1+\sqrt3}{2\sqrt3}=\dfrac{\sqrt3+3}{6}\)
\(A=\dfrac{3+\sqrt3}{6},B=\dfrac{3-\sqrt3}{6}\)
\(f[n]=\dfrac{3+\sqrt3}{6}(\dfrac{4+2\sqrt{3}}{2})^n+\dfrac{3-\sqrt3}{6}(\dfrac{4-2\sqrt{3}}{2})^n\)
\(A=\dfrac{3+\sqrt3}{6},\alpha=\dfrac{4+2\sqrt{3}}{2},B=\dfrac{3-\sqrt3}{6},\beta=\dfrac{4-2\sqrt{3}}{2}\)
\(A=\dfrac{3+\sqrt3}{6},\alpha=2+\sqrt{3},B=\dfrac{3-\sqrt3}{6},\beta=2-\sqrt{3}\)
于是我们似乎把 \(f_i\) 表示成了一个很好的形式,考虑开搞。
\(f_i=A\alpha^i+B\beta^i\)
\(\sum\limits_{i=0}^n\binom{f_i}{k}\)
\(\sum\limits_{i=0}^n\dfrac{f_i!}{k!(f_i-k)!}\)
\(\sum\limits_{i=0}^n\dfrac{f_i^{\underline k}}{k!}\)
\(\dfrac{1}{k!}\sum\limits_{i=0}^n\sum\limits_{j=1}^k(-1)^{k-j}s(k,j)f_i^j\)(斯特林数与下降幂的转化)
(补充:\(x^{\overline k}=\sum\limits_{j=1}^ks(k,j)x^j\))
\(\dfrac{1}{k!}\sum\limits_{i=1}^k(-1)^{k-i}s(k,i)\sum\limits_{j=0}^nf_j^i\)
设 \(g_{n,j}=\sum\limits_{i=0}^nf_i^j\)
\(f_i=A\alpha^i+B\beta^i\)
\(g_{n,j}=\sum\limits_{i=0}^n(A\alpha^i+B\beta^i)^j\)
\(g_{n,j}=\sum\limits_{k=0}^j\binom{j}{k}\sum\limits_{i=0}^n(A\alpha^i)^k(B\beta^i)^{j-k}\)
\(g_{n,j}=\sum\limits_{k=0}^j\binom{j}{k}A^kB^{j-k}\sum\limits_{i=0}^n\alpha^{ik}\beta^{i(j-k)}\)
\(g_{n,j}=\sum\limits_{k=0}^j\binom{j}{k}A^kB^{j-k}\dfrac{1-\alpha^{(n+1)k}\beta^{(n+1)(j-k)}}{1-\alpha^k\beta^{j-k}}\)(等比数列求和)
\(\dfrac{1}{k!}\sum\limits_{i=1}^k(-1)^{k-i}s(k,i)\sum\limits_{j=0}^nf_j^i\)
\(\dfrac{1}{k!}\sum\limits_{i=1}^k(-1)^{k-i}s(k,i)g_{n,i}\)
\(\dfrac{1}{k!}\sum\limits_{i=1}^k(-1)^{k-i}s(k,i)(\sum\limits_{p=0}^i\binom{i}{p}A^pB^{i-p}\dfrac{1-(\alpha^{p}\beta^{i-p})^{n+1}}{1-\alpha^p\beta^{i-p}})\)
小提示:
记得特判等比数列公比为 \(1\)。
代码
#include<cstdio>
#define ll long long
#define mo 998244353
using namespace std;
const int K = 550;
int gen;
int T, op, k;
ll C[K][K], S[K][K], l, r;
ll ksm(ll x, ll y) {
ll re = 1;
while (y) {
if (y & 1) re = re * x % mo;
x = x * x % mo; y >>= 1;
}
return re;
}
struct complex {
ll x, y;
complex(ll a = 0, ll b = 0) {
x = a; y = b;
}
}A, B, alpha, beta;//x+sqrt{y}
complex operator +(complex x, complex y) {
return (complex){(x.x + y.x) % mo, (x.y + y.y) % mo};
}
complex operator -(complex x) {return (complex){(mo - x.x) % mo, (mo - x.y) % mo};}
complex operator -(complex x, complex y) {return x + (-y);}
complex operator *(complex x, complex y) {
return (complex){(x.x * y.x + gen * x.y * y.y) % mo, (x.x * y.y + x.y * y.x) % mo};
}
complex inv(complex x) {
ll fm = ksm((((x.x * x.x - gen * x.y * x.y) % mo + mo) % mo) % mo, mo - 2);
return (complex){x.x * fm % mo, (mo - x.y) * fm % mo};
}
complex ksm(complex x, ll y) {
complex re = complex(1, 0);
while (y) {
if (y & 1) re = re * x;
x = x * x; y >>= 1;
}
return re;
}
void Init() {
C[0][0] = 1;
for (int i = 1; i < K; i++) {
C[i][0] = 1; for (int j = 1; j < K; j++) C[i][j] = (C[i - 1][j - 1] + C[i - 1][j]) % mo;
}
S[0][0] = 1;
for (int i = 1; i < K; i++) {
for (int j = 1; j < K; j++)
S[i][j] = (S[i - 1][j - 1] + (i - 1) * S[i - 1][j] % mo) % mo;
}
gen = (op == 2) ? 5 : 3;
if (op == 2) {
A = (complex){0, ksm(5, mo - 2)}; alpha = (complex){ksm(2, mo - 2), ksm(2, mo - 2)};
B = (complex){0, (mo - ksm(5, mo - 2)) % mo}; beta = (complex){ksm(2, mo - 2), (mo - ksm(2, mo - 2)) % mo};
}
if (op == 3) {
A = (complex){ksm(2, mo - 2), ksm(6, mo - 2)}; alpha = (complex){2, 1};
B = (complex){ksm(2, mo - 2), (mo - ksm(6, mo - 2)) % mo}; beta = (complex){2, mo - 1};
}
}
ll slove(ll n) {
ll ans = 0, jc = 1; ll di = ((k & 1) ? 1 : mo - 1);
for (int i = 1; i <= k; i++, di = mo - di) {
complex sum; jc = jc * i % mo;
for (int p = 0; p <= i; p++) {
complex alphabeta = ksm(alpha, p) * ksm(beta, i - p);
//你是一个一个一个特判啊啊啊!!!
if (alphabeta.x == 1 && alphabeta.y == 0) {//特判公比为1的情况
sum = sum + ((complex){C[i][p], 0} * ksm(A, p) * ksm(B, i - p) * (complex){(n + 1) % mo, 0});
continue;
}
sum = sum + ((complex){C[i][p], 0} * ksm(A, p) * ksm(B, i - p) * ((complex){1, 0} - ksm(alphabeta, n + 1)) * inv((complex){1, 0} - alphabeta));
}
if (sum.y) {printf("f\n"); return -1;}
(ans += di * S[k][i] % mo * sum.x % mo) %= mo;
}
return ans * ksm(jc, mo - 2) % mo;
}
int main() {
scanf("%d %d", &T, &op);
Init();
while (T--) {
scanf("%lld %lld %d", &l, &r, &k); ll sz = (r - l + 1) % mo;
if (op == 2) l++, r++;
else l = (l + 1) / 2, r = r / 2;
printf("%lld\n", (slove(r) - slove(l - 1) + mo) % mo * ksm(sz, mo - 2) % mo);
}
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号