【luogu P4196】[CQOI2006]凸多边形 /【模板】半平面交（计算几何）

update

求两条线段交点的函数似乎错了。。。
而且感觉这种方法不是挺方便的，一开始还要搞个多边形。

于是就写了一个双端队列的版本，代码可以看小凸想跑步的代码。
——>小凸想跑步<——

[CQOI2006]凸多边形 /【模板】半平面交

题目链接：luogu P4196

题目大意

给你几个凸多边形，然后要你求他们交的面积。

思路

首先我们转化一下，我们把点弄成逆时针顺序出现（这道题已经是这样就不用了）

然后我们考虑转化一下，把它转化成求每条线段右边的半平面的交。（如果是顺时针就是左边）

然后就进入正题，如何求半平面交。

---

我们考虑已经维护出一个结果，然后每次加一条边 \((x,y)\)。
然后我们考虑枚举每条边（当然是逆时针顺序）

然后我们考虑一条边 \((a_i,a_{i+1})\)，首先我们考虑怎么会切掉一个点：

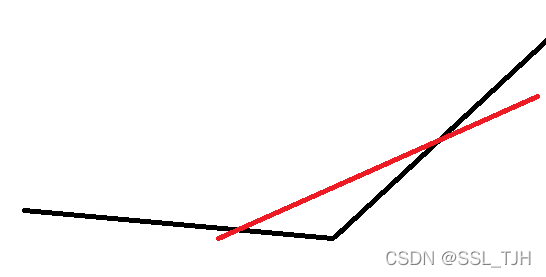
可以看出是被切掉的这个点到这个边的两个点按顺序来讲是顺时针的。
那如果是逆时针或者叉积是 \(0\) 就不会被切。

然后我们每次考虑 \(a_i\) 会不会切，不会就保留，然后看 \(a_{i+1}\)。
如果被切就说明这个交点在这两条边之间，把线段求交的结果加进去，如果不被切就看后面的，先不管。
然后如果 \(a_i\) 被切，就看 \(a_{i+1}\)，如果没有被切就说明交点也在这里。

然后这么搞就好了，可以不用那个双端队列。

代码

#include<cstdio>

using namespace std;

struct node {
	double x, y;
}a[55], b[55], c[55];
int n, m, M, mm;

node operator +(node x, node y) {
	return (node){x.x + y.x, x.y + y.y};
}

node operator -(node x, node y) {
	return (node){x.x - y.x, x.y - y.y};
}

double operator *(node x, node y) {
	return x.x * y.x + x.y * y.y;
}

double operator ^(node x, node y) {
	return x.x * y.y - x.y * y.x;
}

node operator *(node x, double y) {
	return (node){x.x * y, x.y * y};
}

void Add(node A, node B, node C, node D) {
	node AB = B - A;
	node AC = C - A, AD = D - A, BD = D - B, BC = C - B;
	double s1 = AC ^ AD, s2 = BD ^ BC;
	node ap = AB * s1;
	ap.x /= s1 + s2; ap.y /= s1 + s2;
	c[++mm] = A + ap;
}

void Cut(node x, node y) {
	mm = 0;
	a[M + 1] = a[1];
	for (int i = 1; i <= M; i++) {
		if (((x - a[i]) ^ (y - a[i])) >= 0) {
			c[++mm] = a[i];
			if (((x - a[i + 1]) ^ (y - a[i + 1])) < 0)
				Add(a[i], a[i + 1], x, y);
		}
		else if (((x - a[i + 1]) ^ (y - a[i + 1])) >= 0)
			Add(a[i], a[i + 1], x, y);
	}
	
	M = mm; for (int i = 1; i <= M; i++) a[i] = c[i];
}

double Clac() {
	double re = 0;
	for (int i = 2; i < M; i++)
		re += (a[i] - a[1]) ^ (a[i + 1] - a[1]);
	return re / 2;
}

int main() {
	scanf("%d", &n);
	
	scanf("%d", &m); M = m; for (int i = 1; i <= m; i++) scanf("%lf %lf", &a[i].x, &a[i].y);
	for (int i = 2; i <= n; i++) {
		scanf("%d", &m);
		for (int j = 1; j <= m; j++) scanf("%lf %lf", &b[j].x, &b[j].y);
		b[m + 1] = b[1];
		for (int j = 1; j <= m; j++)
			Cut(b[j], b[j + 1]);
	}
	
	printf("%.3lf", Clac());
	
	return 0;
}